|
Beyond Experience: Metaphysical Theories and Philosophical
Constraints, Second Edition, Copyright © Norman Swartz, 2001.
Available for downloading, free of charge, at http://www.sfu.ca/~swartz/beyond_experience. {page 328} CHAPTER ELEVEN Identity-through-time Different philosophers have used a variety of expressions to refer to the concept of identity-through-time. Some writers refer to it as "diachronic identity"; some as "genidentity"; some as "re-identification"; and still others, without qualification, as "identity". The latter term is potentially confusing because it is sometimes also used to refer to the concept of individuation. In this chapter, "identity" is used only to refer to the concept of identity-through-time, never to individuation. 11.1 Is the problem of identity solely an epistemological one? In his landmark book A Treatise of Human Nature David Hume (1711-76) devoted the single longest (by far) section to the topic "Of scepticism with regard to the senses" ([101], book I, part IV, section II). Ostensibly this was a discussion of the grounds for believing in a material external world (of 'objects' or 'bodies' in Hume's terminology) which is the cause of our sensations ('perceptions' as Hume called them). He was, that is, focusing on the inherent difficulties which we mentioned earlier (p. 237) in Locke's theory. Hume adopted a skeptical position. He found that the arguments which would posit objects as the causes of our perceptions were – for him, according to his standards – inconclusive, and hence, he argued, belief in such objects was not rationally well-founded.1 (I have suggested earlier that currently such conclusions as Hume's are less attractive simply because {page 329} we have altered our understanding of what may reasonably be regarded as standards of rational belief.)
But there is another strain running throughout that section of the Treatise which warrants our attention here. Time and again in that section, Hume raises the issue of discontinuous perception. He asks about the existence of objects "even when they are not perceiv'd" ([101], 188), of mountains, houses, and trees "when I lose sight of them by shutting my eyes or turning my head" (194), and of the fire burning in his hearth "when I return to my chamber after an hour's absence" (195). It is easy, in reading these passages, to come away with a totally mistaken notion as to just what the problem of the identity-through-time of material objects is supposed to be. I have known students who, having read these passages, have come to believe that the problem of identity-through-time arises solely through the occurrence of interrupted observation. They have believed – mistakenly – that identity is problematic only when we wish to identify something perceived at some time or other with something perceived at another time and when we have not observed the earlier thing as it continuously 'evolved' into the latter. They have believed that there is no problem of identity if one continuously observes a scene. To subscribe to this belief is to fail to comprehend the depth of the problem. The problem of identity does not come about through interrupted perception. To be sure, the case of interrupted perception complicates ascriptions of identity considerably. But the problem of identity exists even in cases of continuous (uninterrupted) perception. More specifically, the problem of identity-through-time is not a perceptual problem, but a conceptual one. This may be understood by recognizing that even under circumstances of continuous perception, problems of identity arise. There are two such problems. First, suppose no change whatever occurs in one's perceptions over some particular time interval. Let's say, for example, that someone is keeping careful watch on a valued painting. Over a period of continuous observation, five minutes we'll say, no change whatever is perceived to have occurred. Must we conclude that the painting which exists at the end of this interval is the selfsame (numerically identical) painting as that observed at the beginning? We would, naturally, be inclined to say that it is. But really, there are a host of metaphysical assumptions informing our answer. In the Middle Ages, some philosophers believed that physical objects owed their existence to their being 'created'. They also believed that no material object could 'create' another of the same kind, particularly if that other existed at a later {page 330} time. For a material object to exist a minute from now it would have to be created; but no object existing now had within it the capacity to 'create' a similar kind of material object existing at a different (later) time. Thus it was argued that God, and God alone, could create the future object. What may look, on the face of it, to be one material object enduring through time was taken – in this medieval account – to be an infinite succession of material objects, each lasting for only an instant, each created by God in such a manner as to give the appearance (illusion really) of one object enduring through time.2 In such an account, it was impossible to observe a material object over a period of time: there were no such things. Instead what one actually observed were an infinity of successive instantaneous objects. Today this theory of successive creations is no longer seriously credited, but it serves to remind us that it is not a simple 'fact' that we see objects enduring through time. Various medieval philosophers thought otherwise. The point is that the very description "O was perceived throughout the period T1 to T2" presupposes a certain metaphysical theory about the nature of material objects and their existence through time. The merits of that theory are something to be examined, not simply assumed.
The second reason why there is a problem of identity, even under conditions of continuous observation, has to do with precisely the opposite possible results of continuous observation. Suppose now, in contrast, that the 'object' was seen to change in some way: perhaps it grew larger, then smaller; perhaps it changed color, or temperature; perhaps it disappeared from sight (maybe even 'went out of existence') and some time later a qualitatively identical thing appeared. {page 331} What shall we say? Has identity been preserved? Has it been lost? It is clear that the mere fact of observation provides no answer whatsoever to this question. The problem of identity in this latter case has to do with what we want to make of what it is that has been continuously observed. The observing was uninterrupted, but the problem of identity is every bit as severe as in the case of interrupted observation. In short, we need theories to settle questions of identity, not just observations. The problem is principally a metaphysical one, not an epistemological or observational one. 11.2 Is identity incompatible with change? There is a great temptation to regard any change whatever, however slight, as destroying a material thing's identity. For example, if there were to be a scratch, however minute [no pun], on my wristwatch today which was not on my wristwatch of yesterday, there would be an inclination – on the part of some persons – to argue that today's wristwatch could not, strictly speaking, be identified as being the watch which existed yesterday. I have had many students who have argued precisely this thesis. But it is certainly not a modern thesis. It is, we learn, one which has apparently commended itself naturally to many persons since antiquity ([189]). In 1739, Hume commented upon it in his Treatise: Hume has here considered only a change of parts, but he equally well could have been talking of a change in properties. He is making two points: one, that however small a change, 'strictly speaking' that change destroys the identity of the object; and two, that when these changes are in fact small (inconsiderable or trivial), we do not – in our {page 332} ordinary conception of identity – regard these changes as destroying identity. He then goes on to illustrate with several examples how our ordinary notion of identity is invoked through all sorts of changes: the replacement of parts in a ship, the growth of an oak tree, the change in weight of a human being, etc. It would appear, then, that there are two concepts of identity: a 'strict' one and a 'looser' common, ordinary, or everyday one. Perhaps there are, or have been, some philosophers who have adopted this 'strict' sense of identity. Perhaps it was something like this that Heraclitus (6th-5th cent. BC) had in mind when he declared that it is impossible to step into the same river twice. But even if there are a few examples of persons adopting the 'strict' notion and thereby coming to believe that almost nothing endures through time, this 'strict' notion is emphatically not the notion virtually all of us operate with nearly all of the time when we think about identity. The 'strict' notion is a fairly useless notion. Even if, for some misguided reason, one were to adopt it as the 'correct' explication of the concept of identity, it is clear that one would have, almost immediately, to supplement it with another notion, for all intents and purposes the 'ordinary' notion, in order to get on in this world. Virtually everything you own, virtually everything you touch, virtually everything you see changes in subtle (or gross) ways from minute to minute, hour to hour, and day to day. If any alteration whatsoever were to count as destroying that thing's identity, then you could practically never lay claim to owning anything, to touching anything twice, or to seeing anything twice. You could never, for example, have a right to complain of your neighbor's having broken your lawn mower since your lawn mower would not have endured through time in any event: had it been in your own possession, it would have rusted ever so slightly, and that rusting would have destroyed its identity anyway. And so on. It is easy to state conditions for 'strict' identity-through-time: an object preserves a 'strict' identity if it does not change its monadic properties and has no change in parts. But having stated these conditions for 'strict' identity we are now left with the considerably more difficult job of stating the conditions for 'ordinary' identity, the concept we need and use daily to get on in this world where objects undergo constant change, where some of these changes are reckoned not to destroy a thing's identity, and other changes do destroy a thing's identity. (From this point on, we will drop the qualifications "strict" and "ordinary". Hereinafter, "identity" will be understood to refer to 'ordinary' identity.) {page 333} 11.3 Qualitative identity and identity-through-time The problem may be stated formally: under what conditions is O1-at-T1 to be regarded as numerically identical to O2-at-T2? (I stipulate that "T2" always signifies a time later than "T1".) Immediately we must state a profound difference between identity-at-a-time and identity-through-time. In the former case, identity-at-a-time (synchronic identity), it was essential that the objects, O1 and O2, being identified shared all properties in common at T1. But in the case of identity-through-time, where (some) change in properties is given as permitted and indeed something to be accommodated within our theory, we cannot demand that O1-at-T1 have all and only the properties of O2-at-T2. Numerical identity-through-time does not require that the properties of O1 remain the same as it evolves through time to become O2. The situation is a bit more complicated. It may be stated this way:
The first of these principles, (P1), states that if an object O1 at an earlier time T1 is identical with (i.e. is the selfsame object as) O2 at some later time T2, then whatever properties O1 had at T1, O2 – in being the selfsame object as O1 – also had the very same properties3 at that earlier time. But the second of these principles, (P2), states, falsely, that if O1-at-T1 is identical to some object O2-at-T2, i.e. will become over time the latter object, then its properties at the earlier time were the very same as they will be at the later time. To repeat, this second principle is false; an object need not retain all its properties unchanged in order to remain the 'same thing'.
11.4 Parts and properties revisited One theory which suggests itself to many persons is that what identifies {page 334} O2 at T2 with O1 at T1 is that all, or nearly all, of the parts of O2 should be parts that had been those of O1, i.e. that what identifies physical objects is the identity of their parts. Certain sorts of physical objects – e.g. a person's library, or wardrobe (understood as being the clothes a person owns, not the closet in which they are stored), or an heirloom set of dishes – in general the sorts of things which are known as 'assemblages' ([165], 65-6), do seem to be identified by their parts.4
But most physical objects are not assemblages and are not identified by their parts. For most physical objects, the gradual replacement of their parts with fairly similar parts – just like a gradual and relatively minor change in their properties – is compatible with their 'remaining the same thing'. The red car garaged in my carport is the car I bought eight years ago even though in the interim it has had the bulb in the left taillight replaced at least a dozen times,5 has worn out two sets of tires, has had its brakes and exhaust system replaced, etc. And yet, for all that, it remains the same car, and would remain so even if the replacements had been more extensive, e.g. if the engine had been replaced, all four fenders, both bumpers, the seats, the axle, the ignition {page 335} system, the fuel system, the cooling system, etc. There is no part, or any number of parts, whose continued presence is essential to the car's remaining the same car. (Whether every part can be replaced in a thing, and still have the resulting thing remain the same as the original, is a question we postpone until subsection 11.6.3 below.)
But the objection to making the parts of things their identifiers does not rest wholly, or even principally, on the fact that most things are not identified by their parts. The difficulty is more fundamental. The theory that the parts of a thing are its identifier – even for the case of assemblages – cannot be the primary account of identity-through-time but must remain derivative, or parasitic, upon a more basic theory. For the parts of physical objects (recall the discussion on p. 261) are themselves physical objects. To identify a thing by the identity of its parts requires that those parts be themselves identifiable. If parts were identifiable by their parts, and so on, we would have an infinite regress. Eventually, identification by parts must come to an end and we must take recourse to some other, more basic, identifier. 11.5 Positive theories: Substance as identifier Physical objects endure: some for relatively short times, e.g. ice sculptures; others for much longer times, e.g. mountains and planets. But whether they endure briefly or for long, most physical objects undergo change during their existence. They grow and then decay (or are eaten) if they are alive; they tarnish, have parts replaced, and are painted, bent, folded, or spindled, etc., if they are inanimate. Sometimes the changes things undergo are so drastic as to warrant our saying that one thing has ceased to exist and another has come into being, as for example when we sell the family silver serving pieces and allow them to be converted into a photographic emulsion. The (atoms of) silver may endure through such a radical transformation; but the teapot and sugar bowl are gone out of existence, and a new physical object, a photographic transparency, subsequently comes into existence. The material (silver) – or to use an old-fashioned word, the "stuff" – has endured, but the original physical objects whose material it was have not. During its 'lifetime' (the period of its existence), the silver teapot underwent a number of changes. It tarnished constantly and was cleaned monthly. In each of those polishings, it lost a thin layer of silver. Over time, the teapot became successively more scratched. At one point, its spout sprang a leak and had to be resoldered. And five years {page 336} before it was sold, it had been engraved with its owner's insurance number to aid in recovery if it were stolen. And yet, throughout this series of successive and numerous changes, one could reckon it the 'same' teapot. The teapot endured. There is in any such account something that strikes many persons as paradoxical, if not outrightly inconsistent. The very thing which is alleged to have remained the same, i.e. to have endured, is also alleged to have changed. To resolve the conceptual tension, some persons have constructed positive theories which would attribute to enduring physical objects two 'aspects': a deep, or hidden, unchanging permanent 'substance', and an outward, variable set of properties. In such theories, the 'substance' of a physical object is what endures, i.e. persists unchanged through time; what changes are the properties grounded in that substance. Just as substance has been proposed as the individuator (see section 10.3, p. 279, and section 10.5, p. 281), substance has been sometimes proposed as the identifier, i.e. as that 'thing' which confers identity on an enduring object. The many roles often assigned to substance are logically distinct. Even if one were to promote a concept of substance as the solution to the problem of individuation, one would have to argue further for a (perhaps) different concept of substance, or at least for an expanded role for substance, to assert that a thing's substance was what conferred its identity-through-time. Substance, understood as being the 'individuator', need not, it is clear, endure through time. Thus positive theorists might be inclined to supplement their initial account, arguing that not only is it the nature of substance to 'take up space' (i.e. to be extended in space), it is also the nature of substance to 'take up time' (i.e. to be extended in time). But whatever objections there were to positing substance as individuator are paralleled, and indeed even multiplied, in positing substance as identifier. The most obvious problem recalls an earlier objection leveled against substance as individuator: positing substance as identifier does nothing whatsoever to solve the epistemological problem of the re-identification of physical objects. We often have no difficulty whatsoever in re-identifying many familiar objects. I recognize immediately the wristwatch sitting on my desk as being the very same wristwatch I placed on the desk an hour ago. And yet I make the re-identification without being in the slightest aware of the enduring substance of the watch. Indeed, I could not possibly be aware of that substance, if by 'substance' one means 'that constituent of the watch {page 337} which endures unchanged through all incidental changes the watch undergoes'. Certainly no such 'unchanging thing' is given to me perceptually when I examine the watch. But there is another problem as well, having to do not with the epistemological side of the problem, but with the metaphysical. I must confess to not understanding fully what the substance of a physical thing is supposed to be. But whatever it is, it would seem to be something which is spatially coextensive with the object, i.e. is at all places where the object is. But if so, what happens when a physical part of the object is removed from it? Suppose you own a piano and remove one string. Presumably the substance of the piano has been marginally diminished. But suppose you now replace that string with one qualitatively identical to the one removed. The piano with the new string is still the same piano as the one before the swap. (Remember, the goal is to explicate our workaday notion of identity, not a 'strict', artificial notion.) But is the substance of the piano as it exists after the swap the very same substance as that of the piano prior to the exchange of strings? If it is, then it would seem that the substance of the new string has become part of the substance of the piano. This smacks of mysticism. But if we do not claim that the substance of the piano has at first decreased and then increased and indeed latterly been restored, then – according to the theory of substance as individuator – the identity of the piano has been lost: this latest piano cannot be identified, because their substances differ, with the earlier piano. In short, the very concept of substance itself precipitates the very problem it was invoked to solve. For now we should have to have a theory as to how much change a substance might undergo to be deemed to have remained the 'same' substance. In foisting the solution of the problem of identity off onto substance, the metaphysical problem has become aggravated, and the epistemological problem has become insolvable. Clearly, a negative theory is to be vastly preferred. 11.6 Negative theories: Identity without enduring substance Negative theorists will dispense with such unempirical entities as substance. They will attempt to explicate identity-through-time by means of certain relations obtaining between entities existing at successive moments of time. Recall (from section 8.7, pp. 186ff.) the argument that physical objects ought to be conceived as being extended not only in space but in time as well. The task of the negative theorist then {page 338} becomes one of trying to explain how identity is preserved as things change over time. 11.6.1 Space-time pathsThe fundamental concept in the negative theorists' arsenal in their attack on the problem of identity is that of a space-time path. Consider a physical object at rest with respect to its surroundings and undergoing no changes in properties or parts. That is, it is simply 'growing older', and nothing more. Its path through both space and time, its so-called space-time path, is a 'straight line': it is, so to speak, moving straight along the 'time-axis' (see figure 11.1.A, p. 339). But now suppose this object were to rotate about some fixed point. A coin placed on the edge of a rotating disk will do as an example. The coin starts out at a certain place, P1, at a certain time, T1, moves away from that place so that at T2 it is at P2, and eventually returns to its original place, P1, but at a still later time, T3. It then moves away again, and still later returns yet again, and continues to alternate in this manner a great number of times (figure 11.1.B). If, however, we trace the path of the coin on the edge of the rotating disk, not through time alone, where it follows a straight line, and not through space alone, where it follows a circular path, but through space and time together, we discover that it follows a corkscrew (or helical) path (figure 11.1.C). And if someone were to trace your own path, as you move about in space over the course of a day, we would discover that your path through space-time was neither a straight line, nor a smooth corkscrew, but a jagged zigzag of connected segments of unequal lengths and a variety of directions. We can abstract from the notion of the actual space-time paths of actual objects to a generalized notion of a space-time path itself, independent of whether or not anything happens to follow that particular path. Just as there are an infinite number of paths through space connecting any two spatial points,6 there are an infinite number of space-time paths connecting any two positions in both space and time. There are, for example, in principle an infinite number of paths through
{page 339} 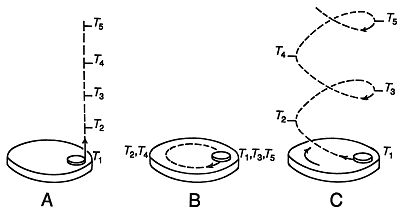
space and time which an object might follow to 'get itself' from the center of London on 11 July 1888 to the dark side of the moon on 18 June 2056. There are a (nondenumerable) infinity of space-time paths. And just as most points of space are devoid of physical objects (see pp. 293-4), most space-time paths are not followed.7 For a path to be occupied means that some physical object, having at least some finite duration in time, follows that path. But of course finding that a space-time path is occupied (or followed) does not mean that some one physical object has endured along that path. A path will be said to be occupied whether one object has followed that path, or whether a succession of different objects has followed that path. For example, a single object, a pumpkin, might follow some space-time path. But it is possible for two or more numerically distinct objects to occupy successive parts of one path. A pumpkin, for example, might miraculously be replaced by a horse-drawn coach. Thus, to explicate the concept of identity-through-time, we will need the concept of an occupied space-time {page 340} path, but we will need considerably more as well. We will need additional distinctions so as to be able to account for the difference between one thing persisting over time and a succession of things replacing one another over time.
For a negative theorist, then, a theorist who eschews substance as identifier, the task becomes one of specifying what sorts of features one must look for in an occupied space-time path to warrant our saying that that path constitutes the history of a single object rather than the history of a succession of different objects. In short, we must look to see what confers unity on one occupied space-time path and diversity on some other. One might begin by thinking that to explicate the notion of a physical object evolving through time and preserving its identity, we need require only that for each point along some space-time path there must be a bundle of properties which is qualitatively identical to the bundle of properties found at every other point along that path. Stating this rather more formally, we might put it this way: CRITERION 1: O2 at (P2, T2) is (numerically) identical to O1 at (P1, T1) if and only if there exists some space-time path connecting (P2, T2) with (P1, T1) such that for every point, Pi and Ti, along this path (including P2 and T2) there exists an object, Oi, which is qualitatively identical to O1.This first criterion is, obviously, too strong: it precludes change. Our ordinary notion of identity-through-time does not require that the later stage of an object be qualitatively identical to its earlier stages. We must find some way to weaken this initial formulation. Before we try, however, there is an important point to be made about the very nature of this particular manner of proceeding which the negative theorist has adopted. Notice how radically the approach of the negative theorist differs from that of the positive theorist. The positive theorist looks for something permanent 'in' the very objects themselves to account for identity-through-time. The negative theorist instead looks not 'within' objects to account for their enduring through time, but looks along a space-time path for certain kinds of features, for a succession of 'stages' as it were, bearing certain sorts of relationships to one another. And yet this is not to have replaced the concept of a single object with the concept of an infinite series of instantaneous objects. Although we have written of "Oi existing at Pi and Ti", where "i" is understood to range over all the infinity of real numbers between those assigned to the starting and end points [i.e. lying between (P1, T1) and (P2, T2)], we need not be thought to be {page 341} describing an infinitude of numerically distinct objects. Recall that it is an implicit understanding, in our use of variables, that different variables may refer to one and the same thing. Although the symbol "O0.24721" may be distinct from "O0.3119872", it remains an open question whether the two objects referred to by these symbols are numerically identical or distinct. They will be numerically identical – according to the negative theory – if they stand in certain important relations to one another; otherwise they will be numerically distinct. One of the necessary relations is that these objects occur along the same occupied space-time path. But considerably more is needed besides. What that 'something more' might be, we turn to next. 11.6.2 Identity-preserving relationsSince qualitative identity is too strong a relationship to insist upon in our attempt to explicate identity-through-time, we might try a weaker relationship, that of qualitative similarity: O1 and O2 will be said to be 'qualitatively similar' if and only if
With the concept of qualitative similarity in hand, we might try to substitute it for qualitative identity in our first criterion. Intuitively, the revised account would be to the effect that at each stage (Pi, Ti ) along a space-time path connecting the earlier object, O1, with the later object, O2, there is an object, Oi, which is qualitatively similar to its immediate predecessor (and successor). But this intuitive notion immediately encounters a certain mathematical difficulty. Although some physicists have occasionally speculated otherwise (see e.g. [211], section 4.5), to the best of our knowledge, time is infinitely divisible; it is, in the terminology of mathematics, continuous. {page 342} This means that for any moment (or instant) of time that one may choose, there is no such thing as the 'immediately preceding' moment or the 'immediately following' moment, since between any two moments there are an infinity of other moments. Immediate predecessor and immediate successor are concepts applicable only to discrete orderings, not to continuous ones. In cases where it is improper to speak of immediate predecessor and immediate successor, mathematicians take recourse to the concept of neighborhood. Roughly (very roughly), we may conceive of the 'neighborhood' of a point as being other points (along the space-time path) which are 'close to that point'.9 Thus, using the concept of neighborhood, we might try the following account of identity-through-time: CRITERION 2: O2 at (P2, T2) is (numerically) identical with O1 at (P1, T1) if and only if there exists some space-time path connecting (P2, T2) with (P1, T1) such that for every point, (Pi, Ti ), along this path (including P2 and T2) there exists an object, Oi, which is qualitatively similar to every object in the neighborhood of (Pi, Ti ).Unfortunately, this latest repair does not quite work. Where the earlier version – in terms of qualitative identity – was too strong, this later version is too weak.
The trouble is that as we trace the successive objects occupying the path from (P1, T1) to (P2, T2), we may find that although stages close together in time may be only slightly qualitatively dissimilar, these differences may accumulate over long time intervals so as to constitute {page 343} wholesale changes between the endpoints. For example, a paper-punch may gradually, over time, be converted into a writing pen. Although 'nearby' stages of the evolving object may be considered to be stages of the 'same' thing, the last point cannot be deemed to be numerically identical with the first.10 Qualitative identity is too strong a relation to require for identity-through-time; qualitative similarity, by itself, is too weak. We shall have to add a further restriction to qualitative similarity.
The counterexample just cited suggests what sort of further restriction is called for. We should want to require not only qualitative similarity, but that at each stage along the path, the object Oi should be the same type of object as those in its neighborhood. It is not enough just to demand that the objects at the endpoints, O1 and O2, be of the same type, for that condition would be satisfied by a paper-punch being transformed into a writing pen, the pen into a bracelet, the bracelet into a scalpel, and the scalpel into a paper-punch. Although the material (or stuff) of the original paper-punch would have been preserved through all these many changes, it seems incorrect to claim that the later paper-punch is the very same punch as initiated the series of transformations. For a later punch to be identified with an earlier punch, it seems entirely reasonable – and consistent with our ordinary notion of identity – to require that the two be joined by a series of intermediate stages all of which are themselves paper-punches. Through a series of successive approximations, we arrive at our third, and final, attempt at formulating a criterion of identity-through-time: CRITERION 3: O2 at (P2, T2) is (numerically) identical with O1 at (P1, T1) if and only if there exists some space-time path connecting (P2, T2) with (P1, T1) such that for every point, (Pi, Ti ), along this path (including P2 and T2) there exists an object, Oi, which is qualitatively similar to each of the objects in the neighborhood of (Pi, Ti ) and which is the same type of thing [tree, wristwatch, piano, leg, etc.] as O1.For convenience, we will hereinafter call this last criterion "the strengthened criterion of spatiotemporal continuity". It is understood to require qualitative similarity as well as identity of kind (i.e. of type or of sort). {page 344} There is an important consequence implicit in our adopting the strengthened criterion of spatiotemporal continuity. On such an explication, there simply does not exist a general account of identity-through-time for a 'thing' which is unqualified as to kind. We can, that is, give an account of the conditions under which a car, or a hammer, or a book is to be regarded as preserving its identity-through-time, but we will not be able to give an account – because none is possible – of the conditions under which a 'thing', in general, i.e. of unspecified type, is to be regarded as preserving its identity-through-time.11
Let us now examine this strengthened criterion of spatiotemporal continuity by applying it to two case studies. 11.6.3 Case study: The ship of TheseusIn legend, Theseus killed the Minotaur; in historical fact, he did not of course: the Minotaur is mythical. Whether Theseus himself is cut from the fabric of sheer myth or was a genuine historical character is quite another matter. Modern scholarship has not been able to settle this question ([210]), although it has identified the historical elements in the legend as occurring in the Bronze Age. Thus when Plutarch (c. 46-120 AD) wrote a biography of Theseus, it would have been at least a thousand years later, ample time for the story to have been considerably altered and embellished. {page 345} Theseus's father was Aegeus, king of Athens. When Theseus was about to set sail from Athens to seek and to try to slay the fearsome Minotaur, he promised his father that on his ship's return, if he had been successful, the black sails would be replaced with white ones stowed on board. But on returning to Athens, Theseus forgot his promise and, although he had slain the Minotaur, did not change the sails. His father, sighting the ship and seeing the black sails, believed his son had perished at the hands of the Minotaur and in his grief hurled himself from a cliff to his death. Theseus, thus, ascended the throne. But at this point in his chronicle, Plutarch pauses for a brief moment. He postpones his recounting of Theseus's subsequent exploits just long enough to tell us something quite curious about the fateful black-sailed ship: "The ship on which Theseus sailed with the youths {page 346} and returned in safety, the thirty-oared galley, was preserved by the Athenians down to the time of Demetrius Phalereus [c. 310 BC]. They took away the old timbers from time to time, and put new and sound ones in their places, so that the vessel became a standing illustration for philosophers in the mooted question of growth, some declaring that it remained the same, others that it was not the same vessel" ([157], Theseus, XXIII.1). Where Plutarch reports that the philosophers' disputes concerned 'growth', we would today understand that it was identity-through-time which was at issue (see [189]). Anyone who adopts the strengthened criterion of spatiotemporal continuity is in a position to give a determinate, and reasoned, answer {page 347} to the puzzle. The ship, with its replaced timbers, is the ship of Theseus. There is an unbroken spatiotemporal path connecting the later, repaired, thirty-oared galley with the original ship. At each point along that path there is a ship (or, more exactly, a ship-stage) which is very like the ships (ship-stages) which are to be found on neighboring (i.e. close-by) points on that same path. We can trace the evolution of the ship through time as timbers are occasionally replaced. But it remains the same ship. (Its changes may be likened to those of the human body where parts [cells] are constantly being replaced, and yet where identity is preserved.) Two millennia after the debate reported by Plutarch, when the problem – which has come to be known simply as 'the ship of Theseus' – was recounted by Thomas Hobbes (1588-1679), we find that a new complicating wrinkle has been introduced. (William Molesworth's translation, dating from 1839, is deplorable. I will paraphrase it.) If the ship of Theseus were continually repaired by the replacing of all the old planks with new, then – according to the Athenian philosophers – the later ship would be numerically identical with the original. But if some man had kept the old planks as they were taken out and were to assemble a ship of them, then this ship [containing all the original parts of the earlier ship] would, also, without doubt be numerically identical with that original. And so there would be two ships, existing at the same time, [in different places,] both of which would be numerically identical with the original. But this latter verdict is absurd. ([97], part II, chap. 11, §7)What we find in Hobbes's version is the head-on conflict of two reasonable theories of identity-through-time. There are good reasons (as I have just rehearsed) for arguing that the ship with the new parts is numerically identical with the original, earlier, ship: it has an unbroken spatiotemporal continuity with that ship. But there are also good reasons for arguing that the ship assembled out of all the discarded parts is numerically identical with the original: its timbers are several hundred years old; it 'looks like' an ancient sea-worn ship; and its parts were present in the original ship. Which one, then, of these latter ships is Theseus's ship? (We will assume that at least one of them is.) It is important not to believe that the resolution of this puzzle depends on some objective truth, some fact which is there to be discovered {page 348} in the way, for example, one might put to an empirical test the question whether today's ship is larger than some other or whether it is painted blue. Hobbes's puzzle is not at all amenable to empirical resolution. For our purposes, all the relevant empirical data are in hand. The question is: "What are we to make of these data?" Ought we to believe that the ship with the new parts is the original? Or ought we to believe that the ship with the old parts is the original? We must choose between two competing – both prima facie plausible – theories. These theories, since they yield conflicting answers, cannot both be regarded as 'right'. But where theories collide and appeal to empirical data is precluded, how is it possible rationally to choose? The decision must rest on weighing the merits and demerits of each theory. For my own part, I am convinced that it is the ship with the spanking new parts, the seaworthy one, not the one recently assembled out of the original parts, which warrants being regarded as the one which is numerically identical to, i.e. is a temporally later stage of, the ship Theseus sailed. A variety of factors inform my choice. First of all is the fact that the strengthened criterion of spatiotemporal continuity is more fundamental than the criterion of sameness of parts insofar as the latter criterion presupposes the former and not conversely. To identify a thing by its parts requires that the parts, at some point or other, be identified by their being spatiotemporally continuous with earlier parts. Other things being equal, the criterion of spatiotemporal continuity takes precedence over the criterion of identification by parts. But are 'other things' equal in this case? If the discarded parts had not been assembled into a ship, then, doubtless, most persons would be willing to allow that the ship with the replaced parts is identical with the original. But the case is not that simple. The discarded parts have been collected and assembled into a ship, and insofar as they have been, might that ship not be a viable contender for the title of 'ship of Theseus', and indeed, might that ship not have the stronger claim? My own reply is to liken the ship assembled from the discarded parts to a cousin laying claim to an inheritance when the deceased has left no will. The cousin is the rightful heir if among the surviving relatives he is the closest in kinship. But let a son or a daughter be factored into the equation and that child then has a stronger claim than the cousin. This is not to say, however, that the claim supported by the criterion of spatiotemporal continuity is absolute or inviolable. Such claims are {page 349} regularly superseded, for example, in the case of assemblages (p. 334). In technical terminology, the priority of the claim sanctioned by the strengthened criterion of spatiotemporal continuity is 'defeasible', i.e. it can be overridden by other, confounding, factors. Might ships, then, be assemblages? Might they be things which we standardly identify by their parts rather than by spatiotemporal continuity? We are certainly not normally inclined to believe so. We standardly treat ships much as we do cars, lawn mowers, radios, etc.: we regard them as preserving their identity even as parts are occasionally changed. But still there lurks the specter of the ship assembled from the discarded parts, with its ancient timbers and leaky hull, faintly calling out for acknowledgment as being the rightful heir to the title 'ship of Theseus'. There can be no verdict in this case which will prove satisfying to every disputant. Persons' intuitions are bound to differ. But there is one further factor which may help to sway some persons toward the claim made on behalf of the repaired ship with its new timbers. Hobbes introduced the wrinkle of having someone collect, and then assemble, the discarded parts. I will introduce a further, final, wrinkle: suppose there were a first mate who lived on board the ship of Theseus and never left it. (He suffers, we may suppose, a debilitating case of terraphobia.) Matey (as he's called) learns that someone has collected the discarded planks from the ship of Theseus and has assembled them into a ship. Matey is totally uninterested. But then Matey learns that this impertinent scavenger is claiming that the assembled ship is the ship of Theseus. Matey is enraged. "That's preposterous", he bellows. "That ship is miles inland. The ship of Theseus has never left the water since the day it was launched. I, myself, have never been off this ship since that day. Since I've never left the ship of Theseus, and since I am here on board this ship, not the one in dry dock, that ship cannot possibly be the ship of Theseus." Who is correct? Were the dispute to end in court, and were I to be on the jury, I would vote for the ship under Matey's feet and not the one assembled inland of the original timbers. Although Theseus himself may never have trod the actual planks of the repaired ship, he did tread its decks, he slept in the captain's stateroom (although never on the present mattress [straw?]), and he took his meals in the galley, although of course not on the wood of the present table. My verdict: the repaired ship is the ship of Theseus even though its parts may not have been present in that earlier ship. The ship assembled from the {page 350} discarded parts of the original is a curiosity, but it is not the historical ship of Theseus. Although its parts are ancient, its history as a ship goes back only a few months: it cannot, then, be the ship of Theseus. Someone might protest, invoking the example of London Bridge. The latter, we know, was disassembled and its parts were carefully numbered, catalogued, and shipped to Arizona. There the parts were reassembled into a bridge standing in the desert at Lake Havasu City. Is this latter structure London Bridge? Certainly. But if so, then how is this case different from collecting the parts discarded from the ship of Theseus and assembling a ship out of those parts? If the structure in Arizona is London Bridge, why is not the recently assembled ship to be regarded as being the ship of Theseus? Again, the analogy with the case of the inheritance of property is apt: the cousin will inherit just so long as a son or daughter does not lay claim. Identity of parts will prevail as the identifier just so long as nothing lays claim to being the spatiotemporal successor of the original. If the ship of Theseus had been disassembled and its parts labeled and catalogued, moved inland, and there reassembled into a ship, then that ship would be the ship of Theseus. But that is not what happened. The original ship was never disassembled. The original ship stayed afloat. The all-important difference is that between replacement and disassembly. In cases of replacement, the criterion of spatiotemporal continuity is paramount. In cases of disassembly and subsequent reassembly, we fall back upon identification by parts. It may seem to you bizarre to explicate the concept of identity-through-time by taking recourse to analogies pertaining to inheritance and the like. You may tend to think of identity as a metaphysical notion totally removed from the conventions of a legal system and of human practices. You may, for example, conceive of the relation of identity-through-time as being more like the relation of being heavier than than like the relation of being before x in line to succeed to the Crown. One may, that is, believe that the criteria for identity-through-time should be something wholly objective, free from any taint of conventionality. The core of the concept of identity-through-time is, in fact, fairly free of conventional trappings. The strengthened criterion of spatiotemporal continuity invokes such concepts as space-time path and neighborhood (in its mathematical sense, not demographic). But even in the core concept, a bit of convention may be seen to be creeping in: qualitative similarity is not a precise notion. There is an unavoidable element of conventionality in our determining what are to count as {page 351} being similar, but not exactly alike, in their properties; or what is to count as comprising 'most' of the parts of a thing. But the strengthened criterion of spatiotemporal continuity comprises merely a necessary condition (and a defeasible one at that) for identity-through-time. In actual cases it must be supplemented with a variety of other conditions. Another example will help to illuminate the nature of these further conditions. 11.6.4 Case study: MitosisHobbes's version of the problem of the ship of Theseus provides an example where two different criteria of identity-through-time – the strengthened criterion of spatiotemporal continuity and the criterion of identity of parts – yield conflicting results. The prospect of mitosis (fission), however, provides an example where the fundamental criterion of identity itself – viz. the strengthened criterion of spatiotemporal continuity – might be thought on occasion to yield conflicting, or at least profoundly problematic, results. Every space-time path has an infinite number of possible (or potential) branch points. In this (the actual) world, physical objects as they follow a space-time path, at arriving at each branch point, pursue one branch to the exclusion of the other possible ones. (Just as a person arriving at a fork in a road may follow one fork but not both.) Of course this fact that physical objects do not split (like the 'coupleton' chairs described earlier [see pp. 301ff.]) is just a contingent fact about this world; it is no necessary truth, which means of course that there are possible worlds where objects do split, i.e. sometimes do follow both branches at a junction point along a space-time path. Amoebae might be thought to constitute a counterexample to the normal behavior of inanimate objects. I remember my biology teacher in high school explaining that amoebae reproduce asexually, by splitting (i.e. by mitosis). He then went on to add the astounding claim that every amoeba alive today "thus was alive twenty million years ago". In other words, my high-school biology teacher subscribed to the theory that when an amoeba splits, each offspring is identifiable with the original, single, amoeba which existed prior to the split. There is a considerable conceptual difficulty inherent in this notion.12 Suppose the original amoeba and its two offspring were to be {page 352} given names: "a", "b", and "c" respectively. If b were to be identified with a and if c were to be identified with a, then b and c would, although in different places, paradoxically be the selfsame thing. (We are here invoking the principle which bears the name 'the Euclidean Axiom', viz. that if y is identical to x and if z is identical to x, then y and z are identical to one another; or, as it is sometimes expressed, 'any two things identical to a third are identical to one another'.) Such a case is radically different from the case, e.g., of the Mississippi River's being in two places at one time, or of a time traveler's being in two different places at the same time. In the case of the Mississippi River, as we have seen, what is involved is two different spatial parts of the river existing in different places at one time. In the case of a time traveler what is involved is two different temporal stages of one and the same person existing at different places at the same time (i.e. the space-time path curves back upon itself). But the case of the amoebae, b and c, is different. The two exist simultaneously at different places; they are each 'complete' amoebae (i.e. they are not spatial parts of a larger organism or of a scattered object); and neither one is a later temporal stage of the other come back in time.
How might we handle such a case? Although there is nothing compelling us to treat it this way, we standardly regard the case of mitosis as the annihilation of the 'parent' organism and the 'creation' (or 'birth') of two offspring. Contrary to the claim of my biology instructor, we do not treat the offspring as identical with the parent. Amoebae alive today were not alive twenty million years ago: their ancestors, of several million generations previously, were alive then; but no amoeba living today was alive then. What this amounts to is modifying the strengthened criterion of spatiotemporal continuity: we will invoke that criterion only for space-time paths where there is no actual branching. An actual branch-point will be taken to mark the end of the existence of one thing, and the creation in its place of two successors. But neither successor will have a claim to being identical with the single 'ancestor' prior to the branching. But if this is the standard manner of handling such cases, must we handle them this way? What if not only amoebae, but tables, chairs, human bodies, etc., were to undergo mitosis? And what if the physical laws of the world were different, so that, for example, objects emerging {page 353} from such a splitting were not half the mass and half the volume of their 'parents' but were qualitatively identical to their parents? How might we handle cases of desks, or chairs, etc. suddenly being replaced by pairs of desks, chairs, etc.? Could there be a concept of identity-through-time in such a world? It would be foolhardy to venture an answer with much insistence. We can have only very tentative grounds on which to predict how we might choose to conceptualize cases which depart so radically from the ordinary. What is important in broaching such cases is not so much anticipating their resolutions, but becoming aware of the extensive penumbra of conditions obtaining in our ordinary use of the concept of identity-through-time. The criterion we have latterly adduced (p. 343) – viz. that identity-through-time requires (i) qualitative similarity along a space-time path and (ii) identity of kind – is well suited for the peculiarities of this particular world. But it is not a criterion which would be satisfactory for any possible set of circumstances whatever. It is, rather, tailor-made by us for this world, a world in which mitosis is nonexistent (or at least a relative rarity) for ordinary physical objects. The problem posed by the prospect of widespread mitosis is not just metaphysical or epistemological. It dovetails importantly with an extensive network of concepts drawn from as far afield as ethics, the law, and economics. For the concept of identity interplays in intimate fashion with questions of ownership and of responsibility and liability. How is ownership to be ascertained? responsibility for damage? If a person owns a boat which spontaneously splits into two boats, would he have a right to claim ownership of both? We can imagine a possible world where the very suggestion would be regarded as outrageous; where it would be 'obvious' that he was morally obliged to choose one and the other would become public property. And what of the person who had damaged the original boat, and failed to repair it before it split into two qualitatively identical (damaged) boats? Would he be responsible for repairing the pair of later boats? We cannot predict how we might handle such an eventuality. Much might depend on how frequently objects split, whether their splitting was foreseeable or not, etc.13
{page 354} 11.6.5 Ineliminable vagueness in the criterion of identityThere are further residual problems with the strengthened criterion of spatiotemporal continuity. Suppose a Volkswagen were to be refashioned, piece by piece, at the Peugeot plant so as to evolve into a Peugeot; and suppose that that Peugeot were then to be refashioned at the Volkswagen plant back into a Volkswagen. There is a space-time path connecting the latter car with the original such that at every stage along the path there is a car. But is the car at the end of this process, even though a Volkswagen, to be regarded as being numerically identical to (i.e. one and the same as) the original Volkswagen? Again I am sure that opinions will differ. Some persons might see in this latter sequence of events certain analogies with the case of, let us say, a house being painted. The later house is identical with the earlier house, even though the earlier one might have been a white house and the later one a brown house. One might try, in light of such an analogy, to argue that the later vehicle is the selfsame car as the original, but is not the same Volkswagen, since at every point along the path connecting the two there was a car, but there was not a Volkswagen. But this answer, we may be confident, will not commend itself to everyone. We can imagine someone arguing, "Being a Volkswagen is not like being white. If a white house is painted brown, and then repainted white again, the later white house is identical with the earlier white house. But if a car is transformed from a Volkswagen into a Peugeot and back into a Volkswagen, it is not to be regarded as the same Volkswagen." Frankly, I do not believe that there is any way a priori to settle this latter debate. I think prephilosophical intuitions are bound to vary from person to person. Some will regard the last car in the series as identical to the first; others will, just as determinedly, regard it as different. If we had a precise, agreed-upon, theory of identity-through-time, we could appeal to that theory to settle the matter. But the trouble is that it is the very theory itself which is at issue. Our prephilosophical intuitions are sufficiently unclear, and differ enough from {page 355} one person to another, as to make it problematic just how we might want to refine our theory further. Philosophical theories are not spun out of thin air. They are devised, first, with an eye to fitting some paradigm cases. If they can be contrived so as to overcome that first hurdle, then – but only then – might they be appealed to in our attempt to settle some borderline disputes. But in the current case, the dispute itself lies not so much at the borderline as it does at the center. We discover, very early on, in trying to formulate an account of identity-through-time, that persons have strongly, if not irreconcilably, different intuitions about identity. It seems unlikely that we could possibly devise a single theory which accommodated such a diversity. It should be pointed out explicitly, however, that the problem we see in the case of the Volkswagen-Peugeot-Volkswagen does not arise from the fact that we have attempted to offer a negative theory. This latter problem would have arisen for a positive theory as well. A positive theorist, confronted with the spectacle of a Volkswagen being transformed into a Peugeot, and the Peugeot in its turn being transformed into a Volkswagen, would be no better off in answering the question whether the latest car is identical with the earliest one. According to a positive theory, the latest car would be identical with the earliest one if and only if the substance of the latest were one and the same with the substance of the earliest. But what is the criterion of sameness of substance through the sorts of changes we have just described? The problem is displaced, but not solved. The problem is a prephilosophical one, infecting any theory whatever that one might try to construct for identity-through-time, irrespective of whether that theory is a positive or a negative theory. If our prephilosophical intuitions are – as I believe – so vague and so variable from person to person as to make selecting a precise theory of identity-through-time arbitrary, then what, if anything, have we accomplished in adducing and promoting the strengthened criterion of spatiotemporal continuity? My own opinion is that this latter criterion – vague as it is – is just about the best we can hope to achieve. This last account offers us the common conceptual core of our concept of identity-through-time. But beyond this point, there is, and can be, no further common (i.e. shared) account. What constitutes identity-through-time for a valued heirloom wristwatch may be strikingly different from that for a wristwatch carrying no sentimental value. What makes the heirloom watch the watch it is, in your regard, is the fact that your father personally {page 356} engraved a message on the back of the watch on the occasion of your twenty-first birthday. Were the back of the watchcase to be destroyed, or replaced, indeed even replaced by a qualitatively identical part complete with a copy of the original engraving, the resulting watch might, as far as you were concerned, simply no longer be worthy of being regarded as the same watch. What is essential, for you, in identifying the watch may be the fact that your father himself engraved the back. Replace that back and what results is a watch, but not the heirloom you treasure. In contrast, your other watch, the one carrying no sentimental value, can have its parts replaced ad infinitum and it would still remain 'the same watch'. Should we allow such variable, such seemingly extrinsic, factors as sentimental value to play a role in determining a thing's identity-through-time? "Isn't the watch really the same (or different)", one might be inclined to argue, "quite independent of anyone's attitude toward the watch? Surely identity-through-time is a determinate notion, not subject to the vicissitudes of anything as variable and unpredictable as persons' attitudes. Virtually everyone else would regard the current watch, with its new back, as being identical with the earlier watch. Surely one person's idiosyncratic predilections cannot carry any weight in determining whether identity has been preserved. Identity is an objective matter, to be settled by objective general criteria, not by one person's sentiment or peculiar requirements." It is a common human failing to be overly ready to dismiss perfunctorily philosophical intuitions and expectations which differ markedly from one's own. It would be easy, and I know that many persons are tempted and some succumb to that temptation, to argue that such properties as sentimental value have no 'proper' or 'legitimate' role to play in a philosophical account of identity. Many persons bring to philosophy the firmly held belief that philosophical analyses should abjure the subjective and should aim for objectivity and determinateness. But that such attitudes may inform, and indeed explain, the manner of someone's doing philosophy does not, of course, justify doing philosophy in that way. One must beware not to mistake one's own convictions as to what a proper philosophical theory ought to look like for a justification for rejecting another's approach. Identity-through-time is a practical concept, tailored by generations of persons to reflect the contingencies of this world, our particular practices of law, our institutions of inheritance and ownership, and our attributions of responsibility and liability. It is naive to believe that it {page 357} can be analyzed in a compact formula, or that there are but a determinate handful of conditions which dictate its use. It is, instead, as complex a notion as any of those of ethics or aesthetics. In saying this of the identity-through-time of material objects, I anticipate the thrust of the next, final, chapter. There I will argue that the concept of personal identity is more complex still, and will argue that far from there being any one determinate concept of personal identity, there is only a core concept to which we then append a diverse array of further conditions. | |||||||||||||||||||||||||
 O2-at-T1 &
O2-at-T1 &
 0
0
 be any positive real number. We define a neighborhood
N(p,
be any positive real number. We define a neighborhood
N(p,  M and
M and
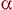 , which Rover also was, and that what has been
preserved in the transformation is a thing of the sort
, which Rover also was, and that what has been
preserved in the transformation is a thing of the sort