Copyright © Norman Swartz 1997
URL     http://www.sfu.ca/~swartz/definitions.htm
This revision: November 8, 2010.  Copyright © 2010.
Department of Philosophy
Simon Fraser University
These notes may be freely reproduced, in whole or in part, provided the copyright notice and URL (at left) are preserved on the copy. Any other reproduction is illegal.



Definitions, Dictionaries, and Meanings

Contents

1 INTRODUCTION
2 USE AND MENTION
2.1 Iconographic and Non-iconographic Names
2.2 Corner-quotes (Advanced material)
3 MOTIVATION FOR DEFINING OUR TERMS
3.1 Exercise
4 SYMBOLIZATION
5 SEVEN KINDS OF DEFINITIONS
5.1 Stipulative Definitions
5.2 Lexical Definitions
5.3 Precising Definitions
5.4 Theoretical Definitions
5.5 Operational Definitions
5.6 Recursive Definitions (Advanced material)
5.7 Persuasive Definitions
6 MODES OF MEANING
6.1 Extension
6.2 Intension
6.2.1 Logically Necessary and Sufficient Conditions
6.2.2 "Intension" explicated in terms of Necessary and Sufficient Conditions
6.3 'Reciprocity' of Intension and Extension
7 PRAGMATICS OF DEFINING
7.1 Contextual Definition (or Paraphrase)
7.2 Defining by Intension
7.3 Defining by Extension
7.3.1 Ostension
7.3.2 Extensional Definition by Naming
7.3.3 Extensional Definition by Unique Description
7.4 Two Case Studies in the Application of the Intension/Extension Distinction
7.4.1 "God exists, by definition"
7.4.2 The 'Width' of an Intensional Definition
8 THEORIES OF DEFINITION
8.1 Theory of 'real' definition
8.2 The Classical Theory of Definition
8.3 The Logic of Criteria and the 'Cluster-Concept'
8.4 The Possibility of an Overabundance of Necessary and Sufficient Conditions
9 DOES "MEANING" MEAN "INTENSION" OR "EXTENSION"?
10 EXPLICATION (/CONCEPTUAL ANALYSIS)
11 CONCLUSION
REFERENCES
NOTES




1  INTRODUCTION

There is a well known motto to the effect that we ought to define our terms. We are often warned that in discussing technical matters it is of the utmost importance to begin by defining the specialized words we will be using.


     Few persons ever call that particular advice into question. There seems to be a self-obviousness to it. Even so, this apparent self-evidence may be nothing more than an outgrowth of our having been taught the adage at a young age before we became philosophically critical.

     Most of us have, in due course, come to be suspicious of – and, if not completely reject, then at least circumscribe – a great number of similar pieces of advice. Few of us as adults are likely to offer unqualified allegiance to such maxims as "Obey the Law" or "Work hard". As mature, reflective adults we have come to see that there are certain circumstances in which these are bad pieces of advice: you should not obey an immoral law, particularly if it is egregiously immoral; and you should not always work hard, if, for example, to do so without overriding need would jeopardize your health or happiness.

     Far too much stock has been placed in the supposed efficacy and utility of defining our terms. Students often approach philosophy with beliefs about definition which border on the magical. Students mistakenly believe that defining one's terms will usually have a powerful, beneficial payoff; but the actual dividend earned in defining one's terms is typically fairly meager.

     For example, suppose a philosophy instructor were to ask the philosophical question: "Can negative events be causes?" There are two ways one might think to invoke definitions in embarking on seeking an answer. The first is completely straightforward and unproblematic. A student might (indeed probably would) be unfamiliar with the technical terminology. A student might never before have heard the expression "negative event" and not know what it is supposed to mean. In such a situation, it would be perfectly appropriate for the student to ask "What does 'negative event' mean?" And the instructor might reply in this sort of way: "By 'negative event' I mean these sorts of things: abstaining from acting; failing to act; neglecting to see, hear, or do something; etc." So far, so good. The reply offered suffices to identify the subject of discourse. But having got that far, a new, much more difficult problem arises. Should abstainings, failures to act, neglected actions, etc. properly be regarded as causes? Are causes to be conceived of as being only classes of actions (or events) or are causes to be conceived of as including certain non-actions (or negative events)? Many students will be quick to answer: "Well, it all depends on one's definition of 'cause'." Does it? Where does one 'find' such a definition? If one were to propose a definition, what are the criteria for having got the definition 'right'? If two philosophers were to offer opposed, or incompatible, definitions how is one to adjudicate between them? Surely it would be arbitrary simply to choose one of them.

     The problem "Can negative events be causes?" like virtually all interesting, challenging problems – both inside philosophy and outside (psychology, biology, economics, history, literary criticism, etc.) – cannot be resolved by offering definitions. The question "Can negative events be causes?" cannot be answered by assuming that there is some 'objective' definition of "cause" against which we can hold up such things as failures to act to see whether or not they qualify as being causes. The actual procedure is, surprisingly, much the reverse. It is, rather, that by looking at problematic cases (such as failures to act) and asking probing questions about how we want to handle such cases, and by offering theories about the nature of causality, that we may come in time to agree upon a 'definition' of "cause". In philosophy, as in many other disciplines, good definitions are the product of lengthy debate, not the starting point.

     Now this may seem exceedingly odd. It may even strike one as paradoxical in the extreme. So wedded have some persons become to the mistaken dictum that they ought to define their terms, that they find it hard to imagine how it is even possible to get started without having first offered a set of definitions. As it turns out, not only is it possible to do so, it is necessary to do so.

     To see this, we must turn away from sloganizing and begin to examine the modern theory of definition. And as we usually discover when we abandon convenient slogans, we find that the truth of the matter is vastly more complicated than we might ever have imagined. We will begin by introducing some of the technical concepts we will need in our studies.
[ Return to Table of Contents ]



2  USE AND MENTION

1. Science begins with curiosity.
2. Science begins with the nineteenth letter of the English alphabet.
Sentence 1 is perfectly sensible (even if what it expresses may be false). But sentence 2 above is a piece of literal nonsense. It is not science itself which begins with a letter; rather it is the word, "science", that begins with a letter. Sentence 2 should be repaired to read:
1'. "Science" begins with the nineteenth letter of the English alphabet.
     To talk (in English) about science (as in sentence 1 above), we use the (English) word which refers to, or names, science, viz. the word comprised of the seven letters "s", "c", "i", "e", "n", "c", and "e". But suppose we want to talk, not about science, but about that very word in English which we use to refer to science. Suppose we wanted to say of that word that it contains seven letters. We might write:
3. The word "science" contains seven letters.
Or, again, suppose now (just to make life complicated) we wanted to talk about the part in sentence 3 which occurs between the words "word" and "contains" (viz. the part with the quotation marks). To talk about that part, we would like a name for it. [Note 1] What is the name for the linguistic part of sentence which consists of the nine items: a left-quotation mark, the letters "s", "c", "i", "e", "n", "c", "e", and a right-quotation mark?

     In the last few hundred years we have developed a technique (effective procedure) in written English (and in many other modern written languages) whereby we can simply and automatically generate the name of any term whatsoever. (Ancient languages lacked this – or an equivalent – technique.) The modern convention in written English for forming the name of a term is to enclose that term in quotation marks. [Note 2] Thus """science""" refers to ""science"" [Note 3] which in turn refers to "science" which in turn refers to science, and at this latter point the relation of referring terminates.

     When we use the name of a term in accordance with the just-reported convention we are said to be mentioning the term. We mention a term, by using its name, where its name is formed by enclosing the term in quotation marks. In the first sentence of this paragraph I used the term "accordance" and it occurred there without quotation marks. And in writing what I just have (in the third sentence of this paragraph) I mentioned the term "accordance" and it occurred there with quotation marks. [Note 4]
[ Return to Table of Contents ]

2.1  Iconographic and Non-iconographic Names

When we form the names of terms by quoting them, we form their names iconographically. We literally picture them. We place a picture of the term to be named within quotation marks. This is an extraordinarily useful technique. It allows us immediately to learn the referent of an iconographic name of a symbol (or word or expression) simply by inspecting that name itself. Consider, for example, the first letter of the Greek alphabet. In English, it has two names, an iconographic one (devised in accord with modern rules for quotation) and an ancient one inherited from times when iconographic names were not available in English. The two names (quotation marks omitted!) are:


Iconographic"α"
Non-iconographicalpha

By inspecting the iconographic name we can learn immediately what the term refers to. No amount of inspection of a non-iconographic term will ever reveal its referent. (Incidentally, we can see in this example another device for quoting, viz. placing the expression in a box. [Yet another technique is to set-off the expression on a separate line and indent it.] If these latter conventions were not available, then properly both of the examples just cited would themselves have had to have been enclosed in quotation marks.) Just to test yourself, try to see that the following claims are correct and accord with the conventions just discussed:

  1. In the expression ""Hi there"", there occurs only a single pair of quotation marks.

  2. However, in the expression """Hi there""", there occur exactly two pairs of quotation marks.

     This convention we have in English of forming the name of a term by the device of enclosing that term within quotation marks is just that, a convention. There is nothing sacred about it. We could if we wanted, agree to use some other device. If we were so inclined, we could agree that the name of George's name would be "Henry" instead of ""George"".

     There is a passage in Lewis Carroll's Through the Looking Glass where he chooses to use a nonstandard device for naming. At first what the Knight is saying to Alice may appear to be literal nonsense. But it is not; it is merely unconventional. However, in addition to adopting a nonstandard manner of naming, Carroll introduces the further complicating wrinkle of distinguishing between the name of an item and what that item is called. Normally we think of these as one and the same thing; persons and things tend to be called by their names. But not always. We do make a distinction between names and nicknames (i.e. what persons are called, if not by their names). For example, we might find ourselves saying, "His name actually is 'Richard', but he's called 'Dick'." [Note 5] When the Knight says (below) that the song is called (rather than named) "Ways and Means", he apparently means that this is the song's nickname. [Note 6] Finally, to make the passage as coherent as possible, we probably should want to understand the sentence "The song really is 'A-sitting On a Gate' " as the Knight's previewing a fragment (the fourth line) of the song that he is about to sing, rather than as an attempt at naming that song.

     "You are sad," the Knight said in an anxious tone: "let me sing you a song to comfort you."
     "Is it very long?" Alice asked, for she had heard a good deal of poetry that day.
     "It's long," said the Knight, "but it's very, very beautiful. Everybody that hears me sing it -- either it brings the tears into their eyes, or else --"
     "Or else what?" said Alice, for the Knight had made a sudden pause.
     "Or else it doesn't, you know. The name of the song is called 'Haddocks' Eyes.'"
     "Oh, that's the name of the song, is it?" Alice said, trying to feel interested.
     "No, you don't understand," the Knight said, looking a little vexed. "That's what the name is called. The name really is 'The Aged Aged Man.'"
     "Then I ought to have said 'That's what the song is called'?" Alice corrected herself.
     "No, you oughtn't: that's quite another thing! The song is called 'Ways and Means': but that's only what it's called, you know!"
     "Well, what is the song, then?" said Alice, who was by this time completely bewildered.
     "I was coming to that," the Knight said. "The song really is 'A-sitting On A Gate': and the tune's my own invention."
     So saying, he stopped his horse and let the reins fall on its neck: then, slowly beating time with one hand, and with a faint smile lighting up his gentle foolish face, as if he enjoyed the music of his song, he began. ([7], Chapter VIII)
To sum up this passage: we have (1) the song itself ([part of which is] "... A-sitting On a Gate. ..."); (2) the (official) name, "The Aged Aged Man", of that song; (3) an (unofficial) nickname (i.e. what the song is called), "Ways and Means"; and finally (4) a nickname, "Haddocks' Eyes", of the name ("The Aged Aged Man").

     In the popular press – newspapers, magazines, etc. – writers and editors will often drop quotation marks, e.g.

"The word equality as used by Mr. Denktash is being misunderstood," responds Greek Cypriot president George Vassiliou. ([24], p. 20)
A strict use of quotations marks, as insisted upon by most writers in philosophy, would require:

"The word 'equality' as used by Mr. Denktash is being misunderstood," responds Greek Cypriot president George Vassiliou.
Philosophers, too, sometimes omit quotation marks. For example, John Stuart Mill writes: "Virtuous, for example, is the name of a class ..." ([16], Book I, Chap. II, §5). Or, again: "Snow, and other objects, receive the name white, because they possess the attribute which is called whiteness" (Ibid). In the latter sentence, Mill omits two sets of quotation marks: one on the word "white"; the other on the word "whiteness".

     The use/mention distinction (as it has come to be called) is of particular relevance in the theory of definitions. For when we give the definition of a term, we mention the term, we do not use it. For example, the term, "pain", is defined, but pain itself is not defined. We define only terms, never their referents.
[ Return to Table of Contents ]


2.2  Corner-quotes

(Advanced material) Suppose you have written a paragraph on a word-processor in which the word "posit" occurs several times and you decide that you want to use your software to search and replace each occurrence of "posit" with the word "hypothesize". If you are not careful, you might create some particularly bizarre results, e.g. you might find that the word "opposite" has been changed into the nonsensical "ophypothesizee". Clearly, when we are substituting on a word-for-word basis, we do not want to substitute within words. In the example just given, we would not want to regard the sequence of letters "p", "o", "s", "i" and "t" occurring within the word "opposite" as a genuine occurrence of the word "posit".

     Quotation marks, as we have just seen in the previous section, create new names. And just as one would not want to substitute for fragments of words (e.g. "hypothesize" for "posit" occurring in "opposite"), one must not substitute for fragments within quotation marks, for to do so one would, in effect, be substituting for fragments within names. For example, suppose you had used the word "wonder" in a paragraph and later decide you want to change it to "awe". If you were not careful, your word-processor might change "She stayed home that evening to watch 'The Wonder Years' on television" to "She stayed home that evening to watch 'The Awe Years' on television". In general, substitution is not permitted within quotation marks. The result of using quotation marks is to create a single cohesive name whose internal fragments are not themselves symbols for which substitution is permitted.

     In certain technical contexts, this prohibition on substitution within quotation marks poses a problem.

     Suppose, for example, that we were trying to state the rules which stipulate the permissible expressions (so called 'well-formed formulas') of a system of logic. We might try writing:

If P and Q are formulas, then "(P & Q)" is a formula.
But this will not do. Suppose we try to substitute specific expressions for P and for Q, e.g. "A" and "~B" respectively. What we would like to obtain from our rule is the following:

If A and ~B are formulas, then "(A & ~B)" is a formula.
Unfortunately, we do not get this latter sentence at all. Since substitution is not permitted within quotation marks, we get instead:

If A and ~B are formulas, then "(P & Q)" is a formula.
To circumvent this problem, mathematicians and logicians have invented a special-duty set of quotation marks – "" and "" – sometimes called "quasi-quotes" and sometimes called "corner-quotes". Corner-quotes act pretty much like ordinary quotation marks except that they do allow substitution in their midst. To capture the intention of the rule discussed above, one would write:

If P and Q are formulas, then (P & Q) is a formula.
From this latter rule, we could derive, as we want, the rule:

If A and ~B are formulas, then "(A & ~B)" is a formula.
(For more on the use of corner-quotes, see [17], pp. 63-66.)
[ Return to Table of Contents ]




3  MOTIVATION FOR DEFINING OUR TERMS

Let us at the outset be very sure that we realize that we can use a term, and use it correctly, even though we cannot define it. Our ability to define terms comes rather late in our linguistic abilities. Children talk, and know what they are talking about, although they cannot define even one of the terms they use. Using and understanding a language does not involve being able to define its terms.

     Well, then, if we can use a language without being able to define its terms, why bother with definitions at all? The answer, put simply, is that language is a tool, and its uses can be extended and improved. Here definition plays a role; it allows us to improve our use of language.

     Specifically, in what ways can definitions refine language? I mention three.
1. Definition can be used to increase vocabulary – to introduce persons to the meaning and use of words new to them.
2. Definition can be used to eliminate some kinds of ambiguity. Examples:
a. "Listen carefully – I can tell this only once because I promised not to repeat it."
b. "Do you believe in altruism?"
c. "He was bent on seeing her."
The offending terms here are "repeat", "believe in" and "bent on". Depending on the intended definitions of these terms the sentences above express very different things.
     When the ambiguity in a sentence depends upon the ambiguity in a term, a judiciously chosen definition can disambiguate the sentence. However, some sentences are ambiguous because of their grammatical construction, and for these sentences definitions do not remove the ambiguity. Here is an example of an ambiguous sentence which contains no ambiguous terms:
d. "He did not kill her because of her dowry."
To disambiguate such a sentence we often rely on a paraphrase:
d'. "He forswore killing her in order to get her dowry."
d". "He killed her, not in order to obtain her dowry, but for some other reason."
3. Definition can be used to reduce vagueness. Many words have borderline uses: "bald", "lazy", "heavy", "clever", "tasty". When is something said to be "big"? Arlene Francis (the 1950s TV personality) used this as her workaday definition: Something is "big" if it is "larger than the average-sized bread box". A meteorologist may define the atmospheric conditions as being "hazy" when nothing can be seen a mile away.




3.1  Exercise

Write down at least two disambiguations (in the manner of d'. and d". above) of the sentence "Many studies have found that stereotypical assumptions are often made about women in the Canadian justice system" ("Clean sweep of sexism on agenda", in The Vancouver Sun [Aug. 17, 1992], p. A1). In each case, explain the source of the ambiguity, i.e. whether it arises in the grammatical construction of the original sentence, whether in the occurrence of an ambiguous term in that sentence, or whether from a combination of the two.
[ Return to Table of Contents ]



4  SYMBOLIZATION

The standard symbol used by philosophers, mathematicians, and logicians for "is [or means] by definition" is "=df". An example is:

"a posteriori" =df "by experience"
The term written to the left of the "=df"-symbol is known by the technical name, the "definiendum" ("that which is to be defined"). The expression occurring to the right, the expression which does the defining, is known as the "definiens".

     The symbol "=df" should be used only between quoted expressions (see the last paragraph in subsection 2.1 above). It would be a (syntactical) mistake, for example, to write:

oxycodone =df dihydrohydroxycodeinone
Rather one would write:

"oxycodone" =df "dihydrohydroxycodeinone"

[ Return to Table of Contents ]



5  SEVEN KINDS OF DEFINITIONS

What kinds of definitions are there? I describe seven here, although I do not suggest that this list is complete.



5.1  Stipulative Definitions

Stipulative definitions stipulate, or specify, how a term is to be used. Sometimes stipulative definitions are used to introduce wholly new terms, othertimes to restrict (or narrow) a meaning in a particular context. The former use may be seen in the immediately preceding example, where the new term "oxycodone" is being introduced as an abbreviation (mercifully) for the mouthful "dihydrohydroxycodeinone". The latter use, where a stipulative definition narrows a use of a term, is found, for example, in some philosophy texts where an author may say something of this sort:

In this book, I will use the term "entails" strictly in this way: to say that "x entails y " is to say that "y logically follows from x ". Other common uses, as – for example – when one says "A severe bout of flu entails a few days of bed rest", will not be used in this book. [Note 7]
     Occasionally authors will stipulate that they intend to use a term in a certain restricted fashion, but as their books unfold, careful readers will detect a reverting to more common meanings. This flaw frequently occurs in books treating such concepts as democracy, culture, perception, explanation, etc. The authors will initially announce that they intend to use a certain term in a restricted fashion, but sometimes within just a few pages they unwittingly fall back to using that term in its ordinary way(s). (The moral is that it is difficult to 'stick to' stipulative definitions of terms – e.g. "intention", "behavior", "meaning", "freedom", etc. – which have well-entrenched usages. There is the constant lure of lapsing into the prose of ordinary speech.)

     Although it is recognized that there are distinct snares in using stipulative definitions to narrow the meanings of common terms, some authors believe that using stipulative definitions to introduce new terms is unproblematic. Copi and Cohen, for example, (persisting with a sentence from earlier editions authored by Copi alone) write in the eighth edition of Introduction to Logic: "One who introduces a new symbol has complete freedom to stipulate what meaning is to be given to it" ([10], p. 132]). Actually, quite the opposite is true. Every time we introduce a new term via a stipulative definition we run the very real risk of introducing internal inconsistency into our language.

     Suppose we take it into our heads to introduce a new operation into arithmetic, an operation symbolized by a star "". We define the star-operation in this manner [Note 8]:

"(m / n) (p / q)" =df "(m + p) / (n + q)"
At first the definition seems innocent enough, but once we start substituting numbers for the variables, quite unacceptable things start to happen. Let m = 1; n = 1; p = 2; and q = 3. We then get:

(1 / 1) (2 / 3) = (1 + 2) / (1 + 3) = 3 / 4
But since 1 / 1 is equal to 2 / 2, we also are entitled to infer that the expression appearing to the left of the first equals-sign is equal to,

(2 / 2) (2 / 3)
This latter expression, however, when spelled out in terms of "+", according to our definition of "", becomes,

(2 + 2) / (2 + 3) = 4 / 5
Thus we have the same expression, "(1 / 1) (2 / 3)" equal both to 3 / 4 and to 4 / 5. Now, two things equal to the same thing are equal to each other. Thus we can write,

3 / 4 = 4 / 5
Multiplying both sides by 20 yields:

15 = 16
And, finally, subtracting 14 from both sides gives us a logically impossible (i.e. a self-inconsistent) result:

1 = 2.
A seemingly innocuous definition has led to a contradiction in our arithmetical system. The addition of this single, ill-chosen definition (of ""), has made arithmetic inconsistent.

     This problem, whereby inconsistency was induced by a poorly chosen definition in (an attempt to extend) arithmetic, is not unique to mathematics or even for that matter just to formal systems in general. Stipulative definition carries with it just as much a risk when used in ordinary language. Suppose I introduce the following stipulative definition,

"ramanda" =df "a house without walls".
If, however, I already have in my language a definition of the following sort,

"house" means by definition "a roofed domicile with four walls",
then the term "ramanda" is (implicitly) self-contradictory; and if I were to go on to say, "Jim has built a ramanda", you would be entitled to infer that Jim has built something which both has four walls and does not have any walls – a conclusion which is patently logically impossible.

     An example of a correct use of stipulative definition may be found in "Causes and Conditions" by John Mackie:

"INUS condition" means "an insufficient but necessary part of a condition which is itself unnecessary but sufficient for the result" ([14], p. 245. On p. 246, Mackie gives a more formal definition of "INUS condition".)

[ Return to Table of Contents ]

5.2  Lexical Definitions

Lexical, or dictionary, definitions are reports of common usage (or usages). Such definitions are said to be reportive (alternatively, reportative) definitions. They are true or false depending on whether they do or do not accurately report common usage. In addition, if the dictionary is published by a prestigious firm and is compiled by competent and respected lexicographers, then the definitions are normative (or regulatory): the definitions both report and regulate common usage. It thus becomes possible to say of a given person that s/he is misusing a particular term. If a person's use of a term is at great variance with how that term is standardly used, and if that person does not stipulate that the term is being used in a specialized nonstandard way, then s/he is using that term incorrectly. [Note 9]

     Let's look to see what one might actually find in a good modern dictionary.

Kind of definition      Definiendum      Dictionary definition
 
SYNONYMS "asteroid" "planetoid"
Comment: Synonym-definition is supposed to be the paradigmatic case of definition but is much rarer than commonly believed.
 
GRAMMATICAL
USE		 "the" "preceding an adj. or adv. in the compar. degree, the two words forming an adverbial phrase modifying the predicate" (Concise Oxford Dictionary of Current English [Note 10] [9])
Comment: This definition does not give a synonym for the definiendum. Note also that "the" occurs three times in the dictionary definition. If a synonym-definition contains the word to be defined, the definition is considered to be circular. But in this case, the dictionary definition is a description of the grammatical use of the word "the". The use in the definition of "the" is here legitimate and probably unavoidable.
 
SPECIES-
GENUS		 "red" "Having, or characterized by, the colour which appears at the lower end or least refracted end of the visible spectrum, and is familiar as that of blood, fire, the poppy, the rose, and ripe fruits" (CODCE)
Comment: This definition makes use of a scientific theory, color theory. But this definition certainly does not state what criteria most persons have in mind when they use the word "red". Persons knew how to use the term "red" long before prisms were invented and before color theory achieved currency. Even today, few persons who use the word "red" know anything about its being the least refracted color in the visible spectrum.

     The definition here helps us to discover an instance of the color red. The first half of this definition is a classical definition in the style of the so-called 'species-genus' variety. The genus is 'color' and the species is the specific color, i.e., the one which occurs at the least refracted end of the visible spectrum. Note that the second half of the definition, where examples are cited, is not exactly correct: surely not all ripe fruits are red.
 
OPPOSITE "pain" "The opposite of 'pleasure'" (CODCE)
 
CAUSE
(implicit)		 "pain" "The sensation which one feels when hurt" (CODCE)
Comment: Again, as in the definition of "red", it is questionable whether this definition is correct. If opposites cannot coexist in the same thing, then pain cannot be the opposite of pleasure. Masochists, for example, find pain pleasurable.
 
CAUSE
(explicit)		 "jaundice" "A morbid condition caused by obstruction of the bile and marked by yellowness of the conjunctiva" (CODCE)
Comment: When people use the term "jaundice", do they usually mean (have in mind) that jaundiced patients have bile obstructions? It is unlikely. Again, as in the definition of "red" (above) we find a definition invoking a scientific theory about which few persons will know. Few persons who use the word "jaundice" 'have in mind' that the condition is caused by a bile obstruction.
 
FUNCTIONAL "hammer" "An instrument having a hard solid head, usually of metal, set transversely to the handle, used for beating, breaking, driving nails, etc." (CODCE)
 
CIRCULAR "odor" "A smell; scent; aroma" (CODCE)
"smell" "Something that is smelled; odor; scent" (CODCE)
"scent" "1. an odor. 2. the sense of smell. 3. a perfume. 4. an odor left by an animal, by which it is tracked" (CODCE)
"aroma" "A pleasant odor; fragrance" (CODCE)
"fragrant" "Having a pleasant odor" (CODCE)
"perfume" "1. an aroma; fragrance. 2. a substance producing a pleasing odor, as a liquid extract of the scent of flowers" (CODCE)
Comment: Definitions in dictionaries may consist of words alone or they may consist of words combined with pictures. (Some dictionaries, e.g. the CODCE, abjure pictures and confine themselves to definitions strictly in terms of words.) Obviously if a dictionary does not include pictures, then either some words are undefined or every word is ultimately defined in terms of itself. Without pictures there is no way to break out of the circle of inter-linguistic definition in a dictionary. But even in using pictures, dictionaries cannot define certain words non-circularly, viz. those that refer to non-visible phenomena, e.g. scents (as we see here in the case of "odor"), pains, sounds, etc. Persons, however, in conversing with other persons, have greater resources available to them than do dictionaries. For persons have ways of directing others' attention to features of the world in ways that go beyond simply calling attention to visual phenomena. (We shall shortly examine the matter of definition by ostension.)


     Uncritically, many persons suppose that dictionary definitions are all of a piece. In fact, however, as we have just seen, they are of a great many different sorts. One philosopher, Richard Robinson, has even gone so far as to suggest that a definition is anything in virtue of which we teach another person how to use a linguistic term.
We need a name for the mere process of imparting the rule that this word means this thing ... And the name marked out for it by the history of language is "definition". Any teaching that a certain word is the name for a certain thing should be called "definition". ([18], pp. 48-49)
Perhaps this is too liberal a proposal for the use of the word "definition". Perhaps the manner of teaching, or imparting, to another person the rule for the use of some term needs to be limited somewhat. Perhaps there are some ways of 'imparting rules' which we might be inclined not to regard as 'giving a definition'. If there are, we can, nonetheless, appreciate the insight which prompted Robinson's sweeping claim: there is no one formula – or even for that matter, just a few formulas – for giving definitions.

     Dictionaries are the handiwork of human beings trying to convey useful information to other human beings about how certain words are used (and, in some instances, misused). [Note 11] Like any other product of human labor, occasionally errors creep in. For example, in the 1974 edition of Webster's New Collegiate Dictionary ([22]) – one of the finest, and most prestigious, dictionaries in the United States – we find the following misbegotten pair of definitions:

"masseur" A man who practices massage and physiotherapy
"masseuse" A female masseur

Apart from the obvious inconsistency (corrected in more recent editions), there is a second problem as well. Note that the definition of "masseur" includes "and physiotherapy". Inasmuch as physiotherapy sometimes goes beyond massage, e.g. to include electrical stimulation of muscles, it is false that every masseur practices physiotherapy, or that practicing physiotherapy is a necessary condition [Note 12] for being a masseur. A masseur may practice physiotherapy, but then again, he may not. More properly, the first definition ought to have been only: "a man who practices massage".

     It bears mentioning that there is no such thing as the dictionary. There are a great many dictionaries on the market today, even more in libraries. Some (e.g. the Merriam-Webster, the New World, the Random House, and the Oxford English) are first-rate; some others are distinctly inferior. (Incidentally, the name "Webster's" is no guarantee of quality. "Webster's" is not a copyrighted name; anyone is free to name a dictionary a "Webster's dictionary". "Webster's" connotes only that a dictionary is one of American [U.S.] English.) However good or prestigious a dictionary, none of them is ultimately 'authoritative': whatever 'authority' any dictionary has is attributable only to the skill and diligence of the men and women who compiled it.

     Dictionaries do not define words; we do. Dictionaries report our standard usages. The definitions in dictionaries are usually little more than helpful 'hints' as to how words are used (i.e. are standardly used among educated speakers and writers of the language). Many persons, however, have misconceived notions of the contents and powers of dictionaries. How many of us have seen letters to editors of newspapers in which correspondents will jawbone opponents by invoking the seeming sanctity and authoritativeness of 'the' dictionary. They will write such things as "the [sic] dictionary defines democracy as 'that system of government in which the citizens vote on issues concerning them' and thus anything less than submitting tax bills to referendum is undemocratic". A case in point:
The Canadian Charter of Rights and Freedoms appears to provide a good foundation for liberty, enshrining it as a right that cannot be infringed by the state unless the infringement is both reasonable and "demonstrably justified in a free and democratic society."
   But something peculiar happened when ... judges started chucking out many activities that the average person would probably expect liberty to include, virtually eviscerating the concept.
   In 1986, for instance, then chief justice Brian Dickson wrote: "In my opinion 'liberty' in ... the charter is not synonymous with unconstrained freedom."
   Well that's an interesting opinion, but it is contradicted by the dictionary. "Liberty" does indeed mean the condition of being free from restriction or control.
— Karen Selick, The Vancouver Sun, 8 September 2010.
Unfortunately, invoking "the[sic] dictionary" carries little weight in such a dispute.

Dictionaries are not designed to adjudicate issues such as the limits of a citizenry's freedoms, nor, for example, whether a given policy is "democratic". Scholars and thinkers write volumes on such matters. It is naive to think that dictionaries, in which definitions are limited to some tens or hundreds of words, could have very much useful to offer on the genuinely weighty concerns of society. Just as no one would think to solve problems in physics or chemistry or medicine by consulting a dictionary, one ought not to believe that one can solve problems in, e.g., philosophy, political science, psychology, etc., by consulting a dictionary.
[ Return to Table of Contents ]

5.3  Precising Definitions

Precising definitions are used to refine the meaning of an established term whose meaning is vague in a context and which needs improving.

     What is a "public disturbance"? No definition covers all the possible circumstances that such a term might cover. The drafters of a law cannot be expected to be able to foresee all the ways it is possible to disturb the peace. Courts of law constantly refine the meaning of the term as new cases occur; they reduce the vagueness – and their decisions become precedents for future reference. Consider also such terms as "public interest", "obscenity", "intelligence", and "disease". A paradigm case-study of a precising-definition has been reported in Time magazine.

The state of Iowa plans to take legal action early next year against any citizen who would 'allow, cause, or permit the emission of objectionable odors into the atmosphere.' But what is the legal definition of an objectionable odor? The six members of the state's air-pollution-control commission have been pondering that question, and at one meeting they even spent the better part of an hour debating whether an objectionable odor exists if no one is there to smell it. They decided that it does.
     In more practical terms, the commissioners decided that an objectionable odor is legally objectionable if it lasts more than three hours, if it occurs more than once in three months, and if it is offensive to 30% of at least 30 randomly selected residents of an area.
     Are these residents accurate judges? The commissioners tested themselves, sniffing wintergreen and amyl acetate (which smells like bananas) to see if they could tell the difference. They could. So they decided to give similar tests and to create a cadre of 'trained noses.' When a citizen complains about an odor, a jury of tested state employees will rush out to sniff and then decide if the law has been violated. (Canadian ed. [Jan. 1, 73], p. 34)

[ Return to Table of Contents ]

5.4  Theoretical Definitions

Some philosophers [Note 13], have portrayed theoretical definitions as if they were unique to science and philosophy and do not occur in ordinary prose. This is an overly restrictive analysis; theories are not unique to science but characterize virtually all our thinking.

     It is true that physicists have given the word "radiation" a heavy theoretical weight to bear – the definition is constructed in light of certain physical theories. But, then, so too is the common word "water". Our use of it is premised on (or alternatively, our use of it presupposes), the well-established belief, or theory, that a certain cluster of properties (e.g. liquidity, transparency, non-acidity, non-causticity, etc.) occur together regularly enough to merit their being given a name: "water". Further, just by calling something "water", we sanction the theoretical implication that the substance will turn to ice when it freezes.

     It is easy to overlook the presence of theoretical definitions in ordinary discourse, precisely because the theories we have at the common-sense level are so well established. But even at this level, theories do change, and consequently, so do meanings. A term such as "disease" simply does not mean the same to contemporary educated persons as it did to the witchcraft practitioners of only a few centuries ago.
[ Return to Table of Contents ]

5.5  Operational Definitions

In the first quarter of the twentieth century, there was an enormous conceptual fracture in physics. Einstein's special and general theories of relativity and the emerging theory of quantum mechanics challenged and eventually superseded the Newtonian view of the world. It is hard today for many persons to imagine how massive a shock the Einsteinian revolution was to scientists who had been taught, and who had done so much profitable work using, the Newtonian theory. To many of those scientists, the new theories seemed outlandish, patently false, and unacceptably counterintuitive.

     In 1927, the physicist Percy Bridgman (1882-1961) undertook a peculiar and ambitious task. He set about looking for a new way of doing physics, one which would prevent scientists from making the sorts of commitments – to one particular view of the world – which would make it difficult for them to accept new theories. He was convinced that there had been something profoundly wrong with the background assumptions in nineteenth-century physics, that the philosophical underpinnings of that earlier science were the cause of the profound difficulty that so many scientists experienced in being challenged by the 'new physics'. Bridgman wanted to create a new philosophy for physics so that scientists would never again have to face such a shift, that they should be able to accept in stride dramatic and radical changes in their theories.

We should now make it our business to understand so thoroughly the character of our permanent mental relations to nature that another change in our attitude, such as that due to Einstein, shall be forever impossible. It was perhaps excusable that a revolution in mental attitude should occur once, because after all physics is a young science, and physicists have been very busy, but it would certainly be a reproach if such a revolution should ever prove necessary again. ([4], p. 2)
Bridgman's proposal was that we should abandon the belief that the fundamental concepts of a science, e.g. length, time, mass (and by extension, anger, intelligence, profit, gross national product, etc.) each referred to a single, unique feature (or property) of things in the world. Instead, he argued, we should conceive of there being as many different, unique, properties as there are means (or techniques or operations) for measuring. For example, instead of conceiving of length as a single feature of physical objects, a feature (or property) which could be measured in a variety of ways, one should think of length-as-measured-by-technique1 (e.g. by a ruler), of length-as-measured-by-technique2 (e.g. by sonar), etc., etc. In short, Bridgman proposed that there is not one single property length, but a whole set of related properties, length1, length2, length3, length4, etc., each arising from a different manner of measurement.

     Why, exactly, Bridgman believed adopting such a revised view of measurement would forestall the very possibility of scientific upheavals is something it is impossible to pursue here. But it suffices to say that Bridgman's so-called 'operational definitions' which were adopted by a few physicists for a time, and by many more psychologists for a rather longer time, eventually came to be seen not only as sterile but as being stultifying to the progress of science. The trouble is fairly apparent. A great variety of physical laws in physics invoke the concept of length (just as many laws in economics invoke the concept of profit, or capital investment, etc.). If each technique for measuring, let us say, length were to produce not a measurement of length per se, but of a different, unique property, then in each instance where we formerly had one scientific law we would now require several. Then, too, there could be no possibility of ever saying that one technique had revealed another one to be inaccurate. For example, suppose one were to proceed in this fashion (as indeed some psychologists did): "What I mean by 'intelligence' is nothing more or less than a subject's score on this particular test. That is, for the purposes of this research design I am stipulating that the operational definition of 'intelligence' just is the subject's score on this test." The trouble should be obvious: if one researcher defines (stipulates) "intelligence" to be (nothing more or less than) the score on one particular test xyz, and some other researcher defines (stipulates) "intelligence" to be (nothing more or less than) the score on some other particular test jkl, then there is no theoretical basis for comparing or contrasting their respective results. There is no overarching theory of intelligence, a single property of which each of these tests, xyz and jkl, are independent measures. There is no way to argue that one test of intelligence is superior to any other test of intelligence since in principle there could not be any two independent tests of the same thing. Similarly, there is no way to predict, on the basis of one of these tests, what it might be reasonable to assume the results of the other will be. In short, the effect of adopting operational definitions is to fragment science, to rend it into countless disparate, isolated facts about countless numbers of unique properties. The fabric of science is unraveled. The ability to generalize in science is destroyed.

     In time, Bridgman came to see the utter counterproductiveness of his proposal. In 1953, he wrote: "I ... have created a Frankenstein" ([5], p. 76). (He was somewhat confused about the monster and the monster's creator. What he obviously meant to say was: "I have created a monster, as did Dr. Frankenstein.") Operational definitions have disappeared in physics; occasionally, however, one will still find instances of them in psychology. Philosophically sophisticated researchers avoid them in their own work and know not to take them seriously in the work of others.
[ Return to Table of Contents ]

5.6  Recursive Definitions

(Advanced material) By a "direct ancestor" we mean one's "parents, grandparents, great-grandparents, etc." More formally, we might write:

"x is a direct ancestor of y" =df "x is a parent of y; or x is a parent of a parent of y; or x is a parent of a parent of a parent of y; etc."
It is clear enough what we mean in this instance, but the inclusion of "etc." in the definiens is regarded as unacceptable according to the standards demanded by mathematicians and logicians. (Even if mathematicians and logicians will occasionally permit themselves the convenience of "etc.", computer programmers can never avail themselves of such a luxury. For digital computers have no ability whatsoever to execute the instruction "etc.") Fortunately there is a way to avoid the problematic "etc.": one can take recourse to recursive definitions.

     The definiens in a recursive definition is (typically) in two parts: a so-called 'basis' clause in which the definiendum does not occur, and a so-called 'inductive step' in which the definiendum does occur. At first the definition may appear to be circular since the definiendum explicitly occurs in the definiens. But the circularity is only apparent, since the basis clause offers a non-circular entry to – not a circle – but a 'chain' of an indefinite number of 'links'. A recursive definition for "direct ancestor" might look like this:

"x is a direct ancestor of y" =df "x is a parent of y, or x is a parent of a direct ancestor of y"
The basis is "x is a parent of y" in which the definiendum "direct ancestor" does not occur; and the inductive step is "x is a parent of a direct ancestor of y". As an example, consider the case of Betty being Alfred's mother, and Carlo being Betty's father. According to the recursive definition just given, since Betty is a parent of Alfred, she is – on the basis clause – a direct ancestor of Alfred. But then it turns out, by a second application of the recursive definition, that Carlo, too, is a direct ancestor of Alfred. To derive the latter result, we use the inductive step in the definition: since Carlo is a parent of a direct ancestor (Betty) of Alfred, then he, too, is a direct ancestor of Alfred. (And similarly for Dorothy, if she were one of Carlo's parents. Etc.) Here are some other examples of recursive definitions:

"x is a number" =df "x is zero, or x is the successor of a number" [Note 14]

"P is known experientially" =df "P is known by direct sense perception, or P is known by valid inference from a set of propositions one or more of which is known experientially"
(For a formal analysis of the concept of recursive definition, see [17], pp. 37-44.)
[ Return to Table of Contents ]

5.7  Persuasive Definitions

Finally we can distinguish persuasive definitions. These are simply intended to influence attitudes and generally do violence to the lexical definitions. When people begin to cite definitions in a heated argument, it is a good bet that they are making them up.

"Democracy" is by definition "the system of government which produces the greatest good for the greatest number".

"Capitalism" means "the system of economic distribution which places the ownership of the means of production in the hands of an entrenched few".

"Logic" is by definition "the study of the means by which to win an argument".

"Government" means "the subjugation of the masses by bureaucrats".

The "function" of the university is, by definition, "to encourage independent thought".

"Barring a miracle, there will be no agreement on a new constitutional package from the federal government. By definition whatever is acceptable to Quebec is unacceptable to the rest of Canada and vice-versa." (Attributed, in [15], to Graeme Decarie, chairman of History at Concordia University.)
Here is an example in which the authors inserted their own bit of editorializing in their definition.
"love"      An emotional state involving attraction, sexual desire, and concern about the other person. It represents the most positive level of attraction. ([2], p. 219)

The latter sentence expresses something highly debatable; the former sentence is readily open to counterexample: it is dubious that parents who love their infants are sexually attracted to them.
[ Return to Table of Contents ]




6  MODES OF MEANING

Philosophers have long utilized (in the theory of definition and in other contexts) the concepts of extension and intension.



6.1  Extension

The extension of a term or phrase is understood to be the timeless class of all things which properly 'fall under' or are described by that phrase. For example, the word "horse" has as its extension all horses – past, present, and future. The phrase "brown horses" has as its extension all (past, present, and future) brown horses (i.e. a proper subset of the former class).

     There are (at least) two common synonyms of "extension". They are: "denotation" and "reference". The members of the denoted class are often spoken of as "the denotata" (sing. "denotatum") or "the referents".

     The extension of a term is fixed: it is not at some time one thing and at some other time something else. The extension of a term includes all past things (if any) plus all present things (if any) plus all future things (if any) that fall under or are described by the term. Thus, although there are no passenger pigeons now (passenger pigeons are extinct), "passenger pigeon" does have a fairly large extension, namely, all the passenger pigeons in the past. The phrase, "female prime minister of Canada", may or may not have an extension. We simply do not know. If it does have an extension, all its members are successors to the present (1992) Prime Minister (a male) and we do not yet know who they are. Note, however, what happens when we add a specific, terminating, historical date to the expression, "female Prime Minister of Canada". The expression, "female Prime Minister of Canada prior to 1972", has a known extension. There never has been, is not now, nor ever will be anyone who satisfies the description, "female Prime Minister of Canada prior to 1972". This latter expression has a zero extension.

     In contrast to "passenger pigeon", which has an extension, we can cite terms, for example, "mermaid", which we are pretty sure have zero extension: i.e. there never have been, are not now, and never will be any mermaids.
[ Return to Table of Contents ]

6.2  Intension

There is a slight problem in defining "intension", the companion notion to that of "extension". [Note 15] Intuitively what we want to capture in our technical definition is the concept of the defining characteristics (sometimes called "the essential characteristics") of a thing. But what are so-called defining characteristics of things? Are we referring to properties or to predicates? [Note 16]

     If, for example, we wanted to state the defining characteristics of triangles, should we regard these as non-linguisitc items, the properties of triangles themselves, e.g. the property of lying in a plane, the property of being closed, the property of having three straight sides, etc., or should we regard these as linguistic items, i.e. predicates, e.g. "lying in a plane", "being closed", "having three straight sides", etc.?

     Historically, the American philosopher C.I. Lewis (1883-1964) called the former of these, the defining properties, "the signification" and only the latter, the linguistic items, the "intension". [Note 17] Subsequently, few philosophers have chosen to maintain Lewis's meticulous care in distinguishing between signification (a group of properties) and intension (a list of predicates). Many writers, in stating the intension of a term (e.g. "triangle"), will cite the properties of a thing (e.g. its having three sides, etc.) rather than enumerate predicates (e.g. "has three sides", etc.). I think their reasons are that they perceive themselves to be defining not just an English term or phrase ("triangle") but its synonyms in other languages as well. I will follow suit. In these notes, too, the difference between signification and intension will not be scrupulously observed below. Strictly speaking, following Lewis's definition, the "intension" of term would be understood to be a list of (defining) predicates. But we will be less than strict; we shall occasionally treat the signification of a term as equivalent to its intension. Strictly speaking, the intension of "triangle" is "being closed, having three straight sides, and lying in a plane". Less rigorously, the intension of "triangle" is (the properties of) being closed, having three straight sides, and lying in a plane.

     One synonym which is sometimes used for "intension" is "connotation". Only if one is careful to abide by its strict technical definition should this latter term be used in these contexts. The trouble is that "connotation" has a well-established, different, meaning in ordinary prose. In ordinary prose, for example, we might find something like this (recalling that quotation marks are frequently omitted in popular writings): "Subsidized housing connotes single-parent families and elevated crime rates". This latter is not the philosopher's sense of "connotes". It is very doubtful that "subsidized housing" has in its intension either "single-parent families" or "elevated crime rates". In its ordinary sense, "connotes" means something like "conjures up images of" or "calls to mind", etc. This is not the technical sense of "connotation" (i.e. of "intension"). Another synonym for "intension" is "designation". Although "designation" is relatively unproblematic, it is (becoming) fairly rare in philosophical writings.
[ Return to Table of Contents ]

6.2.1  Logically Necessary and Sufficient Conditions

Many writers explicate the concept of the intension of an expression in terms of the concepts of necessary and sufficient conditions.

"x is a sufficient condition for y" =df "the presence (/existence /truth) of x guarantees the presence (/existence /truth) of y"


"x is a necessary condition for y" =df "the absence (/nonexistence /falsity) of x guarantees the absence (/nonexistence /falsity) of y"

Examples:

  1. being square is a sufficient condition for being rectangular.
  2. being rectangular is a necessary condition for being square.

  3. being a mother is a sufficient condition for being female.
  4. being female is a necessary condition for being a mother.

  5. having four sides is a sufficient condition for having an even number of sides.
  6. having an even number of sides is a necessary condition for having four sides.
Clearly, as the preceding examples portray, the relations of is a sufficient condition for and is a necessary condition for are converses, i.e. if x is a sufficient condition for y, then y is a necessary condition for x; and if x is a necessary condition for y, then y is a sufficient condition for x.

     There are a great many types (or kinds) of sufficient conditions, and to each there corresponds a type of necessary condition.

     Some conditions are logically sufficient for another. Examples:

  1. having four sides is logically sufficient for having an even number of sides
  2. being a mother is logically sufficient for being female
In such instances, we say that the former term (logically) implies, or entails, the latter. (Put another way, the latter term logically follows from the former.) It would be logically impossible both for the former term to apply to some thing and for the latter term not to apply to that thing. And, naturally, if x is a logically sufficient condition for y, then y is a logically necessary condition for x.

     But some conditions are sufficient for some others without being logically sufficient. A condition might be physically sufficient, or legally sufficient, (or .... psychologically sufficient, or ... palliatively sufficient, or, ... etc., etc. sufficient) for another.

     For example, cutting off all fuel to a gasoline engine is a physically sufficient condition for stopping that engine; but it is not a logically sufficient condition. It is not a logical impossibility that that engine should continue to run under such circumstances: it is only a physical impossibility. (And – although it may sound a bit odd to say it – a gasoline engine's stopping is a physically necessary condition of its having had its fuel supply cut off. This latter claim, strange as it may sound, is a straightforward consequence of the converse relationship which holds between, on the one hand, sufficient conditions, and, on the other, necessary conditions.)

     Similarly, being married to two persons at the same time is (in Canada) a legally sufficient condition to make oneself liable to criminal prosecution. But this is not a case of logical sufficiency, nor is it a case of physical sufficiency.
[ Return to Table of Contents ]

6.2.2  "Intension" explicated in terms of Necessary and Sufficient Conditions

If we look back at the definition of "x is a triangle", we can see that a number of conditions have been specified in the definiens:

  1. x lies in a plane
  2. x is closed
  3. x has (exactly) three sides
  4. x has straight sides
Each of these conditions is a logically necessary condition for x's being a triangle: nothing can be a triangle which failed to satisfy each of these conditions. But no proper subset – no one condition from among these; no pair of conditions from among these; etc. – comprises a logically sufficient condition for x's being a triangle. For surely – to take but one case – something can be both closed and lie in a plane without being a triangle (e.g. it could be a hexagon).

     However, the total set of conditions, 1-4, is a logically sufficient condition for x's being a triangle. Anything that satisfies all four conditions is a triangle.

     The complete set, 1-4, is said to comprise a set of logically necessary and sufficient conditions for x's being a triangle. More specifically: each of the members in the set is said to be 'individually' necessary, and the several conditions – i.e. all of the conditions taken together – are said to be 'jointly' (i.e. 'conjointly') sufficient.

     In giving an intensional definition for a term, we give a set of conditions which are each logically necessary and which are jointly logically sufficient for the correct application of the term. (The foregoing summary, while perfectly correct, raises a number of difficult problems, problems which we will return to later.)
[ Return to Table of Contents ]

6.3  'Reciprocity' of Intension and Extension

There is a certain relationship that holds between intension and extension. As the intension of an expression increases, the class denoted, i.e. the extension, (generally) decreases. For example, the term "black" denotes a certain class. Adding the term "round" to "black", viz. increasing the intension, creates a new expression whose extension is a new, smaller, class, a proper subclass of the former. [Note 18] There are fewer round black things than there are black things. Similarly, there are fewer round, black, hard things than there are round, black things. And so on.

     The foregoing thesis concerning the inverse proportionality of intension and extension must be qualified in various ways.

  1. The extension of an expression never falls below zero. Once the extension reaches zero, further increasing the intension will not reduce the extension.

    Example:
    The expression "black and not black" has zero extension. Increasing the intension to, "black and not black and round" does not further decrease the extension.

  2. Adding to the intension a term which is logically implied by [Note 19] another a term (or terms already present) in the intension, will not decrease the extension. (A corollary: Adding to the intension a term which is logically equivalent to another a term [or terms already present] in the intension, will not decrease the extension.)

    Example:
    Adding "rectangular" to "square swimming pool" does not reduce the extension of the latter expression.

  3. If the presence of one property follows as a matter of physical law from the presence of another, then adding a term naming the second to the term naming the first, does not decrease the extension of the first.

    Example:
    Suppose it is a physical law that all crows are black. If so, then "black crows" has the same extension as "crows" and not a smaller one.
    Example:
    Since it is a physical law that all copper conducts electricity, then adding "electrically conductive" to "copper ingot" does not decrease the extension.

  4. If the membership of a class is infinite, then increasing the intension sometimes can yield another class which is also infinite.

    Example:
    There are an infinite number of numbers [Note 20]; the ordinary number series, "1, 2, 3, .....", 'goes on' without end, i.e. there are an infinite number of members in the series. But curiously the same is true for the series of even numbers, i.e., "2, 4, 6, ....."; it too contains an infinite number of members. The two classes, that of the numbers and that of the even numbers are said to be "equinumerous", that is, both classes contain the same number of members, viz. an infinite number. That there are as many even numbers as there are numbers can be demonstrated by the fact that the members of the two classes can be uniquely 'paired off', or putting the point in more technical jargon, the members of the two classes can be put into a "one-to-one correspondence":
    1 2 3 4 . . . .
    | | | | | | etc.
    2 4 6 8 . . . .
         Increasing the intension of the expression, "number", by adding to it the adjective, "even", to yield an expression of greater intension, "even number", curiously produces a classwith the same number of members as the original class of lesser intension. Obviously the two classes, the one consisting of all numbers and the other consisting of only the even numbers, are not coextensive, that is to say, they do not have identical membership. There are members in the first class which are not present in the second (viz., 1, 3, 5, ...); but every member of the second class does occur in the first. In a word, the class of even numbers is a proper subclass of the class of numbers. But since both classes are infinite, which should we say: that the class of even numbers has a smaller extension than the class of numbers, or that the extension is not smaller? There seems to be little discussion of this point in the philosophic literature and even less widespread agreement. Let us simply stipulate that we shall adopt the first choice. That is, if one class is a proper subclass of another, then that subclass will be said to have a smaller extension even in those cases where subclass and containing class are both infinite. Thus although the class of even numbers contains the same number of members as the class of numbers, we will still say that the former has a smaller extension than the latter.

         Of course, sometimes increasing the intension of an expression having an infinite extension can make the extension finite.

    Example:
    The extension of "number" is infinite; the extension of "even number less than 10 and greater than 6" is very small: it is the number "8"; and increasing the intension of "number" to "even number less than 10 and greater than 16" reduces the extension right down to zero.

[ Return to Table of Contents ]




7  PRAGMATICS OF DEFINING



7.1  Contextual Definition (or Paraphrase)

In a contextual definition we do not give a definition which allows the substitution of one term for another. Rather we give a form of a standard paraphrase such that a sentence or expression in which the term-to-be-defined occurs is replaced by another sentence or expression in which that term does not occur.

Example 1:
"(m / n) (p / q)" =df "(m + p) / (n + q)" [Note 21]
Example 2:
"A is a brother of B" means "A is a male and A has the same parents as B"
Here is Bertrand Russell's famous contextual definition of "the" (adapted from his theory of descriptions [19]):

Example 3:
"The S is P" =df "There is at least one S; there is at most one S; whatever is S is P"
In Russell's definition, we can see that the term "the" appears nowhere in the definiens; and there is no single term or phrase within that definiens which is a synonym for, or a replacement of, the term "the".
[ Return to Table of Contents ]

7.2  Defining by Intension

In this method one specifies a set of logically necessary and jointly sufficient conditions for the application of the term. The clearest examples come from science and mathematics:

Example 1:
"x is a triangle" means "x is a plane closed figure bounded by three straight lines".
Example 2:
"x is a circle" means "x is a locus of a point in a plane lying equidistant from a given point".
Example 3:
"centripetal force" is "the inward force required to keep a particle or an object moving in a circular path" ([20], p. 118)

[ Return to Table of Contents ]


7.3  Defining by Extension

We sometimes define terms by sampling their extensions. (See, e.g., the latter half of the CODCE definition of "red" cited above, subsection 5.2.)

     For example, we might teach a person to use the term "dog" by pointing first to Fido, and then to Rover, and then to Spot. In each case we might say "that's a dog". (Alternatively, instead of pointing, we might cite the names of these animals if the person to whom we are talking knows the reference of the names; or we might use uniquely identifying descriptions to pick out these animals, e.g. "the animal chewing on your slippers", etc.) Then we might point to something else (or name or describe something else), perhaps our cat Tabby, and say "that's not a dog". This is one familiar way that we teach young children to use class names.

     Why do we cite both positive and negative instances? The most common theory offered in explanation proceeds along the following lines. It is theorized (hypothesized) that the person who is trying to learn how to use a given word (most especially a class noun [such as "dog", "chair", "tree", etc.]) will observe the sample case(s) being offered, will note many of its(/their) properties (features, characteristics), and will try to extract (abstract) from these many features just which ones in particular are those in virtue of which we call the thing by its class name. For example, all the dogs mentioned have four legs, and the young child may at first try using the term "dog" to apply to anything that has four legs. But the child who calls the cat "dog" is soon corrected by an adult. Thus the child comes to understand that although Tabby has four legs, Tabby is not a dog. And so the child will revise his/her hypothesis and eventually, having made a series of adjustments, will come to use the term "dog" much as do the adult, experienced, speakers of the language.

     The test whether one has got the 'right' definition in cases of extensional definition depends on one's ability to 'go on': to go on to classify other things, not in the sampled extension, in the 'same way' as the person giving the definition.

     You may note that I have desisted from describing this process as a process which proceeds from a sampling of the extension of a term to a formulation of the intension of that term. Until a decade or two ago, this was the favored way to describe what was going on 'in a person's head' as s/he attempted to plumb the definition of a term when presented with a sampling of its extension. It was theorized that what the person was doing was attempting to create an intensional definition on the basis of the data presented. But this particular theory has come under severe attack in the last generation or two, and we shall have to examine it again, more directly, later in sections 8.2, 8.3, and 9. For the moment, we will be careful not to describe it as a case of forming an intensional definition whenever a person comes to use a term correctly as a result of having been offered a sampling of its extension. It may be that s/he has formed an intensional definition; but then again, perhaps not.

     All extensional definition carries with it the risk that the person to whom the definition is being given will form the wrong idea how others might use the term for cases not present or discussed. For example, suppose you were given the following initial part of a series and were asked to continue the series (this is one sort of test often administered in so-called IQ tests):

1, 4, ...
I suppose two 'rules' might immediately 'leap to mind' (there are of course an infinity of other rules which would do as well): Rule 1: Each number in the series is obtained by adding three to its predecessor. Rule 2: Each number in the series is equal to n 2, where "n" is the number's place in the series, i.e. the first number is 12, i.e. 1; the second number is 22, i.e. 4. According to Rule 1, you would 'predict' the next number to be 7; according to Rule 2, you would predict the next number to be 9. But it turns out that both these 'rules' are incorrect. The next number is revealed to be 16. So it is 'back to the drawing board', so to speak. You need to devise another rule. The series (so far) is:

1, 4, 16, ...
Now what rule(s) might generate such a series? Again you might notice that all the numbers are perfect squares. The series looks to be a series of perfect squares, but with some items (e.g. 9) struck out. What rule might this be? Well, you might try this one: Rule 3: The series is that of the perfect squares with every third item struck out. According to this rule, you would predict that the next item would be 25, the one after that, 49. (The third perfect square, viz. 9, and the sixth perfect square, viz. 36, would be struck out). As it turns out, this prediction about the next few numbers is perfectly correct, and you begin to feel confident that you have found the 'right rule'. But it all comes crashing down eventually. You predict that the series should look like this:

1, 4, 16, 25, 49, 64, 100, 121, 169, 196, ...
But in fact the series continues this way:

1, 4, 16, 25, 49, 64, 100, 121, 196, 256, ...
So you need to try again. Obviously some rule other than Rule 3 is generating the series. But which one? And having found one, there is no guarantee that it will continue to work. (For the rule I am using, see [Note 22].) The point is that given extensionally any class whatever, there are an indefinitely large number of properties that all its members have in common. And, thus, definition by extension logically never suffices to exclude competing alternative hypotheses as to what the unsampled members may be.

     How is it, then, that human beings can ever use this method, and indeed frequently do so with such success? Here one must offer a scientific theory, a theory to the effect that we human beings are physically sufficiently like one another that we will often, after only a few tries, 'come up with' the same sorts of linguistic hypotheses as those of our fellow human beings. In short, the explanation is that we have a built-in (hard-wired perhaps) predisposition to frame similar sorts of linguistic posits as other human beings. For this to be so, it is necessary that we not have potentially infinite capacities for hypothesis generation. From a strictly logical point of view any two things (however seemingly disparate) will have an infinite number of features in common. If we were supremely intelligent (like the angels), it is overwhelmingly unlikely that we ever would in a finite time 'hit upon' just what someone else 'had in mind' when s/he used a particular class noun: for every hypothesis we eliminated, an infinite number of others would come crowding into mind. To learn a language, then, it would appear that one must be intelligent, but not be too intelligent, and that one must have some predisposition to form linguistic hypotheses akin to those formed by one's fellow human beings. [Note 23]

     Whatever the ultimate relationship between one's defining terms by intension and defining terms by extension, we can confidently say this much: definition by intension uniquely determines the extension, but not conversely. Terms with the same extension may have different intensions. For example, the expressions,

"human being"
"two-legged animal that laughs"
"hairless ape"
all have the same extension, yet their intensions are all different.

     Definition by extension – if it is to have any chance at success at all – must, obviously, be limited to those cases which have nonzero extensions. "Unicorn", "mermaid" and "round square" all have the identical extension, the so-called null-set or null-class (the first two as a matter of contingent fact, the third as a matter of logical necessity). Being told that the extension of such-and-such a term is the null-class is not going to be of much help to us when we try to frame an hypothesis as to how other persons use the term.




7.3.1  Ostension

We can sometimes define terms by literally pointing out, or holding up for display, instances of the extension of the term. Holding up an item for display or pointing to an object or feature in our surroundings is commonly said to be an instance of 'ostending' that thing.

     It is useful, however, to adopt a definition of "ostension" which goes beyond simply holding up items for display or pointing to them, for clearly, such a technique is (pretty much) restricted to our visual sense. For our purposes, it is useful to adopt a sense of "ostension" which includes offering an instance of a fragrance or odor so that someone else might come to sense it and hence come to know the referent of some particular word we wish to define, e.g. "lemony" or "mildewed"; or directing attention to a particular sound, e.g. by sitting at a piano and saying (while striking certain keys), "this chord is dissonant"; etc.

     Clearly, definition by ostension is limited. Definition by ostension is restricted to terms whose extensions include members which exist at present or in the very near future and which, further, are in one's immediate vicinity. Living as I do in southern British Columbia, it is not practical for me to define "iceberg" by ostension. And I have been born too late in the history of the world to define "passenger pigeon" by ostension (the last passenger pigeon died in 1914).

     It has been argued by some philosophers that certain terms can be defined only extensionally, terms such as: "red", "blue", "hot", "cold", "salty", "bitter", "sweet", "harmonious", and "dissonant". In a word, all those terms that describe sense-perceptions. Roughly, one can understand these terms only by being presented with instances from their extensions. In the philosophers' jargon, the referents of these terms are knowable only by acquaintance and not by description. (The problem this matter raises is frequently pursued in courses in the philosophy of perception. [Note 24])
[ Return to Table of Contents ]
 

7.3.2  Extensional Definition by Naming, and
7.3.3  Extensional Definition by Unique Description

Where ostension will not work (e.g. the cases of passenger pigeons and icebergs), sometimes other kinds of extensional definitions will.

     Even though there are no U.S. Presidents in my vicinity and even though most of them are either dead or not yet born, I can still name and/or describe all of them up to and including the present incumbent.

     For example one might extensionally define "U.S. President" by naming some of the presidents:

George Washington
     :
     :
     :
Gerald Ford
Jimmy Carter
     Alternatively, we might give, not the names, but unique descriptions of various members:

  • (for Washington) "the commander of the Continental Army at Valley Forge"
  • (for Lincoln) "the author of 'The Gettysburg Address' "
  • (for Eisenhower) "the Allied Commander in Europe in the Second World War"
     Note that in the method of describing members of the extension, it is not always clear whether we are using an intensional definition or an extensional definition. Had we given as one among our definitions, "the chief office holder in the Executive branch of the U.S. government", we would have unwittingly given an intensional definition of "U.S. President".

     Bearing out what I said earlier, we can easily see here that an extensional definition does not logically suffice to determine a term's intension. A person, in surveying the above lists, might hit upon some property other than the intension of the term "U.S. President". For example, all these men were born in the geographical region of (what is now) the United States. [Note 25] But being born in North America is not part of the intension of "U.S. President".

     It is important to understand that the definition of a term defined extensionally (e.g. as in the case of "U.S. President" above) is not the list itself. It is the list of properties (perhaps the intension [if there is one], perhaps not) in virtue of which the list was constructed. If it were the list itself, then any claim about some member not explicitly included in the list being a further member of the extension would be self-contradictory. What we have done is sample the extension. We do not know it in its entirety.
[ Return to Table of Contents ]


7.4  Two Case Studies in the Application of the Intension/Extension Distinction

7.4.1  "God exists, by definition"

Definitions, if used carefully, can be very helpful; but if used poorly or unwarily can lead to gross confusions. For example, some persons have uncritically thought that they could legislate facts by means of definitions. One so-called 'proof' of the existence of God is a case in point:

"God" means by definition "the existent, all-knowing, all-powerful, loving creator of the world." From the very definition of "God" it follows that God exists. Therefore, God exists.
This argument is very attractive and some persons have been convinced by it, but the argument is fallacious: its conclusion does not follow from its premise.

     Let us not worry whether the stated definition of "God" is correct or not, that is, let us not be concerned whether this definition reports what most persons understand by the word, "God". For our purposes we can regard it as a stipulative definition.

     Why, exactly, is it that we cannot validly infer that God exists from the definition of "God", even though "God" is defined to be – among other things – "an existent being"?

     Simply: we cannot legislate into existence by means of definitions things which do not exist. This is not to say that God does not exist, only that if He does, it is not because of our concocting a particular definition.

     Recall that adding a term to an expression can have the effect only of leaving the extension unchanged or decreasing it, it cannot increase it. If the expression, for example, "spherical, black, hollow and weighing 160 tons", has a zero extension, then adding the term, "existent", onto the expression does not bring the thing described into existence. Suppose that we assign a name to the object just described. We define the term "haaversphere" to mean "an existent, black hollow sphere weighing 160 tons". The term "haaversphere" is perfectly meaningful; it is even part of the very definition of "haaversphere" that haaverspheres exist (just as it is part of the definition that haaverspheres are black). But that the term "haaversphere" is meaningful, and further that it includes the very notion of existence, does nothing finally to guarantee that there are in fact any actual haaverspheres. If this 'trick' worked, we could effortlessly, simply by concocting certain definitions, bring into existence anything imaginable. Alas (or perhaps fortuitously!?) the world does not work that way.

     If "all-knowing, all-powerful, loving creator of the world" happens as a matter of fact to have a zero extension, then adding "existent" onto that expression cannot raise the extension – nothing exists which has the latter description if nothing exists which has the former.

     The upshot: the term, "God", may mean (stipulatively) "an existent all-knowing, all-powerful, loving creator of the world", but it does not follow that anything answering to this description exists. The term, "God", may be meaningful, but God may not exist. Whether God exists or not cannot be decided or legislated by a definition.
[ Return to Table of Contents ]


7.4.2  The 'Width' of an Intensional Definition

In trying to construct an intensional definition for a term whose extension is known or roughly agreed upon, we should like the definition to 'fit' the extension as closely as possible.

     If an intensional definition admits more members to the extension of that term than would normally be thought to belong there, the definition (using a geometrical metaphor) is said to be too wide or too broad. For example, suppose we wish to construct an intensional definition for the term "religion". We can picture the class of religions as a circle with points in it representing various religions (e.g. Christianity, Judaism, Hinduism, Islam, Taoism, and Buddhism).




Suppose now that we try to construct an intensional definition. We might try, as a first attempt, D1: "a specific system of belief". It would be clear that such a definition would include the entire extension of "religion" (as pictured above), but would also contain a great many more, extraneous things.




(Of course, some persons have suggested that Communism, Science and Astrology are religions and such persons would be content with this first definition. But for the majority of English speakers, Communism, Science and Astrology are not regarded as religions; most persons would reject this first definition. It is not a reportive definition, but it is one [if seriously put forward] which can at best be described only as "persuasive".) This first attempted intensional definition is, then, too broad: it admits too many members to the extension.

     Since the extension of a term can be reduced by increasing the intension, the obvious thing to do in this case is to add one or more terms to the evolving definition. We might, for example, try to specify the precise content of the beliefs mentioned in the first definition and thus produce D2: "a specific system of monotheistic beliefs". This second definition has a far smaller extension than the first, but the trouble is that it has too small an extension. We have succeeded in collapsing the extension below the limits we would like.




The beliefs embodied in Hinduism and Buddhism are not aptly described as being "monotheistic"; in effect our definition is now too narrow: it excludes things which properly are members of the extension of the term, "religion".

     What we desire in constructing an intensional definition for a term whose extension is fairly well agreed upon is one which is neither too narrow nor too broad. To find such is not always an easy task. And, as we shall see presently, sometimes not possible at all.

     Curiously, an intensional definition can be both too wide and too narrow. (Here we depart from the geometrical concept of "width".) A definition is both too wide and too narrow if it both admits things to the extension of a term which do not properly belong there and excludes things which do. An example would be defining "religion" as D3: "a specific system of kinship taboos". Of course some religions do incorporate kinship taboos, but not all do (definition too narrow); and some things other than religions (e.g. legal codes) also incorporate kinship taboos (definition too broad).

     Returning to our models, we can picture the case of a definition which is both too broad and too narrow as a class which partially overlaps the class specified in extension.




If it is not already clear, perhaps it should be mentioned explicitly that what we are looking for is an intensional definition such that the class it determines coincides with the class specified antecedently in extension (remembering of course that typically one never specifies the entire extension but only a sample thereof). (The model would consist of one circle superimposed on another.)

     Two problems are provoked by this discussion of the concept of "width". The first, and most obvious, concerns the problem of 'fitting' an intensional definition to a class fairly well specified in extension. This problem involves the so-called "Classical Theory of Definition" and its contemporary revisions. The second problem arises out of those cases in which we try to construct an intensional definition for classes whose extension is not agreed upon, that is to say, those cases in which we try to construct an intensional definition for a vague term. This latter problem will bring us to that curious and distinctly philosophical enterprise called "explication".
[ Return to Table of Contents ]




8  THEORIES OF DEFINITION



8.1  Theory of 'real' definition

Early philosophers, in particular Plato and Aristotle, advanced a theory of real definition. To them, definitions were something to be discovered in some absolute metaphysical realm. Words had a 'true' (or 'correct') meaning which could be discovered. It would make sense, therefore, to say that everyone misused a word – a conception which can hardly be countenanced today.

     We all know that the term, "pound", in North American (typically) is used to refer to a standard measure of weight, while in England it is also used to refer to the standard unit of the monetary system. But suppose someone in reflecting on this fact were to ask us, "Which is the real meaning of 'pound', that having to do with weight or that having to do with money? What does 'pound' really mean?" We in turn would have to reply that such a question was badly confused. "Pound" does not 'really mean' the one or the other; there simply are no such things as 'real meanings' independent of the ways persons use terms. The meanings of terms are relativized to groups of language users – one group may use a term in one way and another group in another. A small group may use a term in a nonstandard way; but not a very large group. Large groups of persons, especially if they contain well-educated persons, set the norms of usage and consequently of meaning. The answer to the question, "What does the term 'pound' mean?", can be answered only by reference to a group of language users. Simply, it means one thing to North Americans and another to the English. There is no one 'real' or common meaning. It means what we (or others) make it mean and nothing else.

     On this modern theory, when we talk of 'discovering the definition of a term' we mean discovering what criteria (what rules or formulas [perhaps intension]) the bulk of language users actually use in applying the term.
[ Return to Table of Contents ]


8.2  The Classical Theory of Definition

The so-called 'Classical' theory of Definition is a theory of modern philosophy. (It should not be confused with the theory of 'real' definition above. The Classical theory rejects the theory of 'real' definition.)

     The Classical Theory of Definition has two principal tenets: (1) that a 'proper' intensional definition states in the definiens the logically necessary and sufficient conditions for the application of the definiendum; and (2) that there are intensional definitions for each of the class terms (e.g. "horse", "house", "musical instrument", "educated person", etc.) which we use.

     Since we have been able to offer examples of intensional definitions above, there are, obviously, some clear-cut and relatively unproblematic cases readily available that satisfy this theory of definition. Paradigm cases are readily found in mathematics; there (as we have already seen) we find intensional definitions laid out as logically necessary and sufficient conditions for the definiendum: (to repeat) "'triangle' means 'a plane, closed figure, bounded by three straight lines'". Each of the conditions specified in the definiens is individually logically necessary; and the conditions taken altogether (i.e. jointly) are logically sufficient. The definiens tells us precisely under what conditions something is properly called a "triangle", and under what conditions something is not to be called a "triangle".

     There is an important relationship between the two pairs of concepts, breadth and narrowness, on the one hand, and necessary and sufficient conditions on the other. Consider the various necessary conditions just listed. The first necessary condition specified for a thing's being properly called a "triangle", i.e. lying in a plane, is obviously in and of itself far too broad to serve as a definition of "triangle". But as more and more other necessary conditions are added to the intension of the definiens, the extension of the definiens systematically diminishes. The definiens shrinks to the requisite degree of narrowness when it first lists enough conditions to comprise a sufficient condition for a thing's being properly called a "triangle". Any definition which specifies the necessary and sufficient conditions for the application of the definiendum has precisely the right 'width': it is neither too broad nor too narrow; it 'fits' the extension perfectly.

     The example of a triangle is well suited for an analysis in terms of necessary and sufficient conditions. For many persons, over many many years, geometry and mathematics have always provided the paradigm examples of knowledge and techniques of reasoning. Somewhat uncritically, on the basis of this model, people believed that comparable definitions could be constructed in more ordinary contexts, that definitions of ordinary class terms – not just those in mathematics and science – ought to specify the necessary and sufficient conditions for the application of the definiendum.
[ Return to Table of Contents ]


8.3  The Logic of Criteria and the 'Cluster-Concept'

It is only in relatively recent times – in the last half-century or so – that the Classical Theory of Definition has been challenged. Ludwig Wittgenstein (1889-1951) criticized this theory in his Philosophical Investigations ([23]). There he asks what are the necessary and sufficient conditions for a thing's being a game. [Note 26]
§66. Consider for example the proceedings that we call "games". I mean board-games, card-games, ball-games, Olympic games, and so on. What is common to them all?--don't say: "There must be something common, or they would not be called 'games'"--but look and see whether there is anything common to all.--For if you look at them you will not see something that is common to all, but similarities, relationships, and a whole series of them at that. To repeat: don't think, but look!-- Look for example at board games, with their multifarious relationships. Now pass to card-games; here you will find many correspondences with the first group, but many common features drop out, and others appear. When we pass next to ball-games, much that is common is retained, but much is lost. --Are they all 'amusing'? Compare chess with noughts and crosses [tic-tac-toe]. Or is there always wining and losing, or competition between players? Think of patience. In ball games there is winning and losing; but when a child throws his ball at the wall and catches it again, this feature has disappeared. Look at the parts played by skill and luck; and at the difference between skill in chess and skill in tennis. Think now of games like ring-a-ring-a-roses; here is the element of amusement, but how many other characteristic features have disappeared! And we can go through the many, many other groups of games in the same way; can see how similarities crop up and disappear.
     And the result of this examination is: we see a complicated network of similarities overlapping and criss-crossing: sometimes overall similarities, sometimes similarities of detail.
As we can see, Wittgenstein examines many possible suggestions – winning or losing, being amusing, requiring skill, requiring luck, requiring more than one player, etc. – as to the common element in games and finds them all wanting in one way or another. Boldly he concludes that there simply are no necessary conditions which are common to all games, i.e. which each and every game must have in order for it to be a game. Instead of there being a set of necessary and sufficient conditions, common to all games, Wittgenstein suggests (§67) that what is involved is a set of 'family resemblances': threads of common features running among the many things we call "games". Some of these threads overlap with others, some crisscross, some are long, some are short, etc.

     Let's try to work out our own case to see what sort of thing Wittgenstein's metaphor amounts to. I propose we try to define the term "lemon" [Note 27]. We begin by listing some of the characteristics lemons typically exhibit. Lemons typically:

1. are yellow 10. are internally segmented
2. are sour 11. are pulpy
3. are ovoid 12. have a pocked surface
4. grow on trees 13. are green prior to maturation
5. are as big as a ten-year old's fist 14. grow in a semitropical climate
6. are juicy 15. have a waxy skin
7. have internal seeds 16. contain vitamin C
8. have a peculiar (lemony [Note 28]) aroma 17. are edible
9. have a thick skin 18. other ... ?


With this rather long list before us, can we proceed to construct a definition of "lemon" that satisfies the classical theory?

     First we ask whether there is any item on the list which is a necessary condition for calling a thing a "lemon". Is being yellow? Suppose we find something which in all other respects except its color, which happens to be pink, is just like all the lemons we have ever encountered. Would we call it a "lemon"? More than likely. But if so, being yellow is not a necessary condition for a thing's being called a "lemon". Similarly for virtually any other item in the list. If a thing resembled lemons as we now know them save it were sweet instead of sour, we probably would still call it a "lemon". And so on and so on. The upshot of the argument is that few, if any, items on the list are necessary conditions. Virtually any one could be abandoned and we might still call the object which exemplified all the rest a "lemon". Perhaps we might even let some pairs of items be deleted, or maybe even some threesomes. (Even so, obviously some items are more important than others.)

     Clearly if an object exemplifies every item on the list it properly can be called a "lemon": the entire list is jointly sufficient. But the list is overdetermined; something less than the entirety might also be jointly sufficient.

     In summary, few, if any, items in our list are necessary and something less than the entirety is jointly sufficient.

     It would seem, then, that what it is to be properly called a "lemon" is to score fairly well in most of the various categories.

     But if this is so, how are we to construct a precise (more exactly, an intensional) definition? How are we going to capture in our definitions the vague notions of "score fairly well" and "most"? The classical theory did not allow the intrusion of these vague qualifying terms; yet they seem to be unavoidable in the present case.

     The answer favored by many (perhaps most) philosophers nowadays is that we cannot construct a classical definition for "lemon". The term, "lemon", is a so-called 'cluster-concept' [Note 29] – it is made up of a number of conditions which generally are not singly necessary and are jointly oversufficient.

     There is no doubt that all of us are able successfully to use the word "lemon" and we could 'go on' classifying various things as lemons or not. But because all the lemons we have ever seen have been yellow, we have never had to ask ourselves whether something which is orange could properly be called a "lemon". We have not had to ask whether being yellow is a strictly necessary condition for a thing's being called a "lemon". Thus in one sense we do not know the definition of "lemon": that is, we cannot give a classical intensional definition for it. Yet it would be absurd to say that we do not know what "lemon" means. Of course we do. The concept, lemon, is a cluster concept, and we know the conditions in the cluster and we are fairly well agreed on their relative importance.

     It should be clear that classical definitions are possible for only a relatively minute number of terms. Virtually all the sophisticated classificatory terms that we use mark out 'clusters' of characteristics and not hard-and-fast lists of characteristics. Typically we know very well what "lemon" means, what "religion" means, what "school" means, what "table" means, what "story" means, etc. But any attempt to define "lemon", "religion", "school", "table", or "story" by means of a specification of necessary and sufficient conditions will do violence to the accepted extension. If we attempt to specify a single list of necessary and sufficient conditions for the application of the definiendum, we will be faced with this dilemma: Either (1) the list of conditions will be too long (the intension will be too narrow) and consequently will eliminate from the extension various members which properly belong in the extension but which fail to exemplify every necessary condition mentioned, or (2) the list of conditions will be too short (the intension will be too broad) and thus will admit into the extension various things which properly belong outside of it but which do succeed in satisfying the set of jointly sufficient conditions specified. There is little prospect of specifying a single set of individually necessary and jointly sufficient conditions which marks out the same extension as a cluster-concept constructed from those same conditions.

     In short, very often we know the extension of a term very well, we can even 'go on' reasonably well, yet we are unable to specify the intension, and moreover ought on many occasions to resist the demand that we try to give an intensional definition for the term.
[ Return to Table of Contents ]


8.4  The Possibility of an Overabundance of Necessary and Sufficient Conditions

We have just seen in the preceding case study (of "lemon") that it is sometimes impossible to find a set of necessary and sufficient conditions for the application (i.e. proper use) of a given term. Much less remarked in the philosophical literature is the possibility of finding more than one set of necessary and sufficient conditions, a possibility which raises further doubts – but from the 'opposite direction' as it were – about the thesis that there is a (i.e. exactly one) proper intensional definition for each class noun.

     Consider the case of "square". What is 'the' intensional definition of "square"? Here are five competing candidates, i.e. sets of logically necessary and jointly sufficient conditions.

  1. "square" =df "a plane closed figure that has exactly four sides all of which are straight and equal to one another and whose interior angles each measure 90o"

  2. "square" =df "a plane closed figure having four straight sides and whose diagonals are both equal in length to one another and bisect one another at right angles"

  3. "square" =df "a straight-sided, plane, closed figure, every diagonal of which cuts the figure into two right isoceles triangles"

  4. "square" =df "an equilateral parallelogram containing no (interior) acute angles"

  5. "square" =df "an equilateral parallelogram containing four axes of symmetry"
The first of these may be the closest (fairest) representative of what most persons 'have in mind' when they use the term "square", but the other four 'definitions' also 'pick out' the identical extension. If the former is to be privileged as being the one to earn the accolade "'the' intensional definition", it cannot be on its logical features alone: it can be regarded as 'the' intensional definition only by invoking empirical data about language-users' tacit rules.
[ Return to Table of Contents ]




9  DOES "MEANING" MEAN "INTENSION" OR "EXTENSION"?

[... to be written ...]
[ Return to Table of Contents ]



10  EXPLICATION (/CONCEPTUAL ANALYSIS)

Philosophers are not lexicographers. In analyzing concepts, philosophers do not often content themselves simply with reporting how terms are standardly used. To do so would be to engage in 'pure' (or 'narrow') analysis. More often, philosophers offer very sophisticated 'reconstructions' of concepts. While a lexicographer may use some dozen or more (perhaps even a few hundred) words in defining, e.g., "knowledge", a philosopher, in contrast, may offer a journal article, a chapter, or even a lengthy book. The philosopher's 'analysis' (often called "explication"), which may be thought of as being a 'broad' analysis, contains a very substantial element of proposal: it is, in effect, a theory how we might profitably conceive of some particular concept or of some set of interrelated concepts. For example, this very set of notes may be viewed as an attempt to give a broad analysis (explication), not a short dictionary definition, of such concepts as definition, meaning, and even of explication itself.

     In 1950, Rudolf Carnap (1891-1970) offered an insightful explication of the concept of explication ([6], pp. 3-8). He introduced a pair of technical terms – "explicandum" and "explicatum" (most other authors prefer "explicans" in place of the latter) – which are obvious analogs of the familiar "definiendum" and "definiens". [Note 30] Carnap argued that there are four constraints on a philosophical analysis. The explicans is to be
  1. similar to the explicandum
  2. as exact as possible
  3. fruitful
  4. as simple as possible
Carnap insisted that as one goes about trying to offer an explication of some given concept, one's effort must be thoroughly informed by the ordinary, pre-philosophical understanding of the concept (the explicandum). Philosophical reconstructions do not take place in an intellectual vacuum. Virtually any concept worthy of a philosopher's interest has a rich and varied use in ordinary prose. Philosophers cannot depart too far from this 'home base' without doing excessive violence to that ordinary concept. The task is a delicate balancing act: to try to preserve as much as possible of the original concept while at the same time trying to improve it, remove vagueness, make it more precise, etc. If the explication is successful, then – at least for philosophical purposes – the explicans comes to supersede, i.e. to replace or displace, the pre-analytic explicandum. For example, just as the statistician's analysis of "probable" replaces, within statistics, the cruder, ordinary concept, and the physicist's concept of "weight" replaces, within physics, the cruder, ordinary concept, so too the philosopher's analysis of "implication" replaces, within philosophy, the ordinary concept.

     Unfortunately, but not unexpectedly, there is no agreed-upon way of balancing, or even of measuring, the various 'dimensions' (desiderata) in an analysis. What one philosopher offers as an analysis of some particular concept, another may find departs too far from the ordinary use of that concept, while yet another may find remains too closely wedded to the ordinary use. What one may find too precise, another may find too imprecise. What one may find too simple, another may find not simple enough. And so it goes. There is no mechanical way to go about judging the correctness or acceptability of a philosophical proposal.

     There is, to be sure, a certain component of truth in an explication. Whether a proffered analysis (explication) succeeds in capturing much of the ordinary concept is a question which permits – at least to a certain degree – of a determinate answer. But whether the analysis is precise enough for philosophical purposes, whether it is fruitful enough, and whether it is of the desired degree of simplicity, are questions about which we can expect perennial dispute.

     Recall the example with which we began this set of notes, viz. the one having to do with whether negative events can be causes. I suggested that were one to attempt to answer such a question by stipulating at the outset some definition of "cause", then one's answer would, in effect, be question-begging. There is no ordinary, or pre-philosophical, ready-at-hand definition (or analysis) of "cause" which would allow us to answer such a question. Rather, in order to answer such a question, we must engage in a very great deal of philosophical analysis: we must look to see how the concept of cause is ordinarily used (in a great many contexts, in physics, in the law, in day to day affairs, etc.) and look to see whether this explicandum can be 'captured' in a single unified explicans or only in a family of interrelated explications. (Certain analogs to features in the earlier case of "lemons" should be apparent.) But philosophers will disagree even as to the starting points, i.e. as to what the explicandum should be taken to be. Some will see certain uses of the concept of cause as being more 'basic', e.g. some will see the concept of cause as it occurs in atomic physics as being the 'core' notion; but others will regard the concept of cause as it occurs in our own deliberative bringing about changes in the world as being the core concept (these latter philosophers frequently talk of causes as being 'recipes' or [metaphorically] as being 'levers'). Unfortunately, there are no non-arbitrary ways of settling such debates. There are no objective criteria for judging philosophical analyses. Pluralism in philosophy – just as in politics, religion, and (as we have learned in the last 50-75 years) in science, too – is an unavoidable fact of life.

(For more on explication, see [6], pp. 3-8 and [21], pp. 100-107.)
[ Return to Table of Contents ]




11  CONCLUSION

Defining our terms and analyzing our concepts are not panaceas for our philosophical woes – often these techniques produce results which are even more controversial than the problems which prompted their use. These are techniques which must be used gingerly, with care, and with an understanding of their limitations and a watchful eye both on their potential for clarification and elucidation and on their potential for distortion and the disregarding of distinctions. Like all other philosophical tools, defining terms and analyzing concepts are no better or worse than the skill of the persons wielding them.
[ Return to Table of Contents ]

REFERENCES

[1] Aune, Bruce, "Intention", in [11], vol. 4, pp. 198-201.
[2] Baron, Robert A., and Donn Byrne, Social Psychology: Understanding Human Interaction, 5th ed., Allyn and Bacon, Boston, 1987.
[3] Belnap, Nuel D., "Tonk, Plonk, and Plink", in Analysis, vol. 22 (1962), pp. 130-4. Reprinted in Philosophical Logic, ed. by P.F. Strawson, Oxford University Press, London, 1967.
[4] Bridgman, Percy W., The Logic of Modern Physics [1927], Macmillan Co., New York, 1961.
[5] ______, "The Present State of Operationalism", in The Validation of Scientific Theories, ed. by Phillip G. Frank, Collier Books, New York, 1961, pp. 75-80.
[6] Carnap, Rudolf, Logical Foundations of Probability [1950; 2nd edition 1962], University of Chicago Press, Chicago, 1962.
[7] Carroll, Lewis (pseudonym for Charles Lutwidge Dodgson), Alice's Adventures in Wonderland and Through the Looking Glass [originally published 1865 and 1871 respectively], New American Library, New York, 1960.
[8] Chisholm, Roderick M., "Intentionality", in [11], vol. 4, pp. 201-204.
[9] Concise Ox ford Dictionary of Current English, ed. by H.W. Fowler and F.G. Fowler, 5th ed., Oxford, 1964.
[10] Copi, Irving, and Carl Cohen, Introduction to Logic, 8th ed., Macmillan, New York, 1990.
[11] Encyclopedia of Philosophy, ed. Paul Edwards, Macmillan, New York, 1972.
[12] Gasking, Douglas, "Clusters", in The Australasian Journal of Philosophy, vol. 38, no. 1 (May 1960), pp. 1-36.
[13] Lewis, Clarence Irving, An Analysis of Knowledge and Valuation, The Open Court Publishing Company, La Salle, Illinois, 1946.
[14] Mackie, John, "Causes and Conditions", in American Philosophical Quarterly, vol. 2, no. 4 (Oct. 1965), pp. 245-264.
[15] Maser, Peter, "Sovereignty vote unlikely, experts say", in The Vancouver Sun (Dec. 28, 1991), p. A9.
[16] Mill, John Stuart, A System of Logic: Ratiocinative and Inductive [originally published 1843; 8th ed. 1872]. Reprinted by Longmans, Green and Co., London, 1965.
[17] Pollock, John L., Technical Methods in Philosophy, Westview Press, Boulder, Colorado, 1990.
[18] Robinson, Richard, Definition [originally published 1954], Clarendon Press, Oxford, 1962.
[19] Russell, Bertrand, "On Denoting", in Mind (1905). Reprinted in Bertrand Russell, Logic and Language: Essays 1901-1950, ed. by Robert Charles Marsh, George Allen & Unwin, London, 1956.
[20] Stephensen, R.J., "Centripetal force", in McGraw-Hill Encyclopedia of Physics, ed. Sybil P. Parker, McGraw-Hill, New York, 1983, pp. 117-118.
[21] Swartz, Norman, Beyond Experience: Metaphysical Theories and Philosophical Constraints, University of Toronto Press, Toronto, 1991.
[22] Webster's New Collegiate Dictionary, 7th ed., G. & C. Merriam Company, Springfield, MA, 1974.
[23] Wittgenstein, Ludwig, Philosophical Investigations [originally published 1953], trans. G.E.M. Anscombe, Macmillan, New York, 1962.
[24] Zintl, Robert T., "So Near and Still So Far", in Time (Sept. 16, 1991).

[ Return to Table of Contents ]


NOTES

  1. A name is not essential. We can, of course, refer to the part, as I have just done, by description. We could refer to it as "the part in sentence 3 which occurs between the words 'word' and 'contains'".
    [ Resume 1 ]
  1. Quotation marks, insofar as they are regarded as punctuation marks - like commas, periods, semi-colons, etc. – are not spoken aloud. (More exactly, they are not usually spoken aloud; Victor Borge has made a living speaking pronunciation aloud as part of his stage performance.) Thus it is rather clumsy in spoken English to create the names of words. We have to take recourse to such awkward expressions as: "She knew that quote mind unquote was not much used in his course."
    [ Resume 2 ]
  1. It is common when using quotation marks inside of quotation marks, to switch the inner pair to single-quotes, e.g. "'science'". (See also footnote 25, for another example.) In the U.K., the convention is often reversed from that most commonly used in North America. Many writers and editors in the U.K. will use single quotation marks for 'outer' quotation marks, and double quotation marks for 'inner' ones.
    [ Resume 3 ]
  1. There is another, related, use of quotation marks among careful, serious writers. Sometimes writers will place (single) quotation marks around a word or a phrase to indicate that they are using the term in a specialized or idiosyncratic way. (See e.g. the quotation marks on the word "word" in footnote 25 below.) Such marks are often called "scare quotes", "shudder quotes", or "inverted commas". Again, the convention is often reversed in the U.K.: there the usual convention is to use double quotation marks for scare quotes.
    [ Resume 4 ]
  1. In the Bible there is a recurring, odd, phrase: "... called the name ...". (See, e.g., Genesis 21:3: "And Abraham called the name of his son that was born unto him, whom Sarah bore to him, Isaac.") Today we would say (using quotation marks around the name) either "... called the child '...'" or "... named the child '...'".
    [ Resume 5 ]
  1. A genuine example of this distinction can be found in the case of Oscar Straus's operetta, The Chocolate Soldier. There is in that operetta a famous aria which many persons call "I Love You Only"; its actual name is, however, "My Hero".
    [ Resume 6 ]
  1. Note that, strictly speaking, the expressions "x entails y" and "y logically follows from x" should be within corner-quotes, not ordinary quotes. Can you see why?
    [ Resume 7 ]
  1. This example is adapted from one by Guiseppe Peano (1858-1932). (Cited by Belnap in [3].)
    [ Resume 8 ]
  1. I know of no good dictionary that currently (1992) sanctions the use of the 'word' "alot". Yet a great number of persons do write "alot" for "a lot". Perhaps in a generation or two, we will find that "alot" has become acceptable usage and that it will appear among the accepted words in good dictionaries.
    [ Resume 9 ]
  1. Hereinafter abbreviated "CODCE"
    [ Resume 10 ]
  1. Richard Robinson writes: "Lexical definition is a form of history" ([18], p. 35).
    [ Resume 11 ]
  1. The concept of necessary condition will be examined more fully below, in section 6.2.1.
    [ Resume 12 ]
  1. For example, Copi and Cohen ([10], p. 137).
    [ Resume 13 ]
  1. An example: according to this recursive definition of "number", three is a number because three is the successor of the successor of the successor of zero.
    [ Resume 14 ]
  1. Beware. There is another term, viz. "intention", which is deceptively similar and which, therefore, poses a pitfall for the unwary. In ordinary prose, we often use the latter term, saying for example, "It had been her intention to study hard, but she found that she knew the material without studying it." (In philosophy, there are still further, different, uses of the term "intention". See, e.g., [1] and [8].) In the theory of definition, however, it is "intension" – the companion, or contrasting, term to "extension" – which is our concern. Sometimes philosophers – to signal the difference in spoken dialogue between the two concepts – will use the expression "s-intension" for "intension", and – naturally – "t-intention" for "intention".

         If there weren't difficulty enough in the potential confusion between the two words "intension" and "intention", it must be pointed out that the terms "intension" and "extension" are used in a variety of ways in philosophy. In these notes we use "intension" and "extension" strictly as defined above, i.e. as modes of meaning. But be aware that these terms are also used in some quite different senses as well, including serving as synonyms for "truth-functional" and "non-truth-functional" respectively.
    [ Resume 15 ]

  1. The distinction is this: redness, for example, is a property of physical objects; redness is not a linguistic item; redness does not, for example, exist in English but not in French, in fact redness does not exist in any language, it is not a linguistic item. In contrast, "redness" is a predicate naming the property of redness; "redness" – unlike redness – is a linguistic item; "redness" does exist in English and does not exist in French; in French, the synonymous term is "rougeur". Predicates are linguistic items and are unique to specific languages.
    [ Resume 16 ]
  1. Lewis in fact distinguished yet another, a fourth, 'mode' of meaning: the "comprehension" of a term. "The comprehension of a term is the classification of all possible or consistently thinkable things to which the term would be correctly applicable" ([13], p. 39). We will not have need in these notes for the concept of comprehension.
    [ Resume 17 ]
  1. "Adding" here means conjoining. When we add (or conjoin) "round" to "black", we mean "round and black". If we were to disjoin a term to an intension, e.g. move from "black" to "round or black", the resulting extension might very well increase.
    [ Resume 18 ]
  1. i.e. is entailed by, or logically follows from
    [ Resume 19 ]
  1. Throughout this Example, by "number", I mean "natural number", i.e. a member of the set consisting of the number one and all of its successors (2, 3, 4, ..., etc).
    [ Resume 20 ]
  1. See subsection 5.1.
    [ Resume 21 ]
  1. The rule I used to generate the series of numbers in section 7.3, is:
    Each number in the series is generated by squaring an integer provided that that integer is not a multiple of any number which (when expressed in the decimal system) ends in the digit "3", i.e. the numbers in the series are squares of the integers excluding
    3, 6, 9, 12, 15, 18, 21, 24, ...
    13, 26, 39, 52, 65, 78, 91, ...
    23, 46, 69, 92, 115, 138, 161, ...
    33, 66, 99, 132, 165, 198, 231, ...
    ., ...
    ., ...
    ., ...
    [ Resume 22 ]
  1. You might want to reflect on the assumptions being made, about human cognitive abilities, by persons who use tests of the sort just described in the previous pargraph in their devising of IQ tests.
    [ Resume 23 ]
  1. Before we leave the matter of the definition of sensory-predicates entirely, we might just amuse ourselves with an aside raising another problem from the philosophy of perception. The latter problem concerns our apparent inability to describe a difference which many of us take to be intuitively obvious. It seems to be an accidental matter of fact that we see with our eyes and hear with our ears, for we can easily imagine Martians, for example, seeing with organs that do not resemble eyes. What it means to see does not depend on our having eyes. But if so, then what is the difference between seeing an apple fall to the ground and hearing it fall? It can not be just that one sees with one's eyes and hears with one's ears. We can imagine the Martian seeing and hearing with one sense organ. But if we can't use the difference in sensory organs as the explanation, what can one use to explain the difference? Philosophers have been puzzled by this problem. Is there perhaps something deeply wrong with the question itself?
    [ Resume 24 ]
  1. This is not to say that they were U.S. citizens. George Washington, one may recall, like several of the other early Presidents, was born a British subject in North America.
    [ Resume 25 ]
  1. See especially §§65-71, §§79-80.
    [ Resume 26 ]
  1. As I recall, the idea to use "lemon" for this exercise originated with Michael Scriven. The list of features which follows below, however, is the handiwork of some of my own former students.
    [ Resume 27 ]
  1. When we wish to describe the color of lemons we do not need to make reference to any physical objects, least of all to lemons. We do not need to say that lemons have a peculiarly 'lemony color'; we can say simply that they are yellow. The case of describing aromas is different, however. In the latter instance we do not seem to have the object-neutral language that we have in the case of colors. 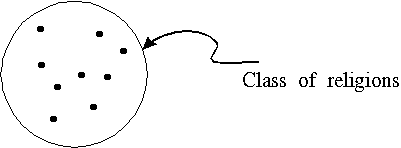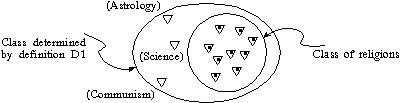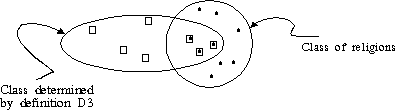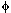We cannot say lemons have a -aroma, where "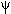" names one among many aromas which just happens to be exemplified in lemons. Almost all our descriptions of aromas are of the sort: "it smells as 's typically do", where "" is the name of a kind of physical object.

         The precise reasons why we have an enormously elaborate color-vocabulary and virtually a nonexistent aroma-vocabulary has puzzled most philosophers at one time or another. The question is sometimes pursued in advanced courses in philosophy, in particular, in the philosophy of perception.
    [ Resume 28 ]
  1. The term "cluster concept" was coined by Douglas Gasking [12].
    [ Resume 29 ]
  1. (Some authors prefer "analysandum" and "analysans" to "explicandum" and "explicatum" (/"explicans".) "Explicandum" and "explicans" should not be confused with "explanandum" and "explanans". The former two are technical terms in the theory of analysis and mean, respectively, "that which is to be explicated (analyzed)" (i.e. the pre-philosophical, ordinary concept) and "that which explicates"; the latter two are technical terms in the theory of explanation and mean, respectively, "that which is to be explained" and "that which explains". We explain an event, e.g. what caused the vase to be knocked off the table; we explicate a concept, e.g. the concept of causality.
    [ Resume 30 ]




I welcome your comments, suggestions, and criticisms. Please email me: Norman Swartz.

Return/transfer to Norman Swartz's Philosophical Notes

Return/transfer to Norman Swartz's Home Page