Possible Worlds: An introduction to Logic and Its Philosophy
Copyright © Raymond Bradley and Norman Swartz, 2010
Answers to exercises on pages 30, 35 and 40-41
|
Exercise on page 30
Question: Can two propositions be contraries as well as contradictories of one another?
Explain your answer.
Answer: No. Suppose that G and H are contraries of one another. Then (according
to the definition of "contrariety" [see top of page 29]) they cannot both
be true (i.e. ~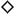 (G & H)) but
they can both be false (i.e. (G & H)) but
they can both be false (i.e. 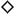 (~G & ~H)).
But contradictories cannot both be false (that is, there is no possible world
in which they are both false; in each possible world, they have opposite
truth-values). Thus no propositions which are contraries of one another are
also contradictories of one another. (~G & ~H)).
But contradictories cannot both be false (that is, there is no possible world
in which they are both false; in each possible world, they have opposite
truth-values). Thus no propositions which are contraries of one another are
also contradictories of one another.
|
Exercise on page 35
- "Q is a false implication of P" means that Q is false and that Q is an implication of P.
In symbols:
~Q & (P  Q) Q)
"It is false that P implies Q" means that P does not imply Q.
In symbols:
~(P  Q) Q)
- Let
"J" = "Jean Chretien [the former Prime Minister of Canada] has more than 29 children."
"K" = "Jean Chretien [the former Prime Minister of Canada] has more than 18 children."
K is a false implication of J. That is, K is false, and J implies K, i.e.
~K & (J  K) K)
- Let
"M" = "Jean Chretien owns a bicycle."
"N" = "Margaret Thatcher likes to arrange flowers."
It is false that the former implies the latter, i.e.
~(M  N) N)
|
Exercises on pages 40-41
1.
Inconsistency
- a is inconsistent with iv
- c is inconsistent with i
- c is inconsistent with ii
- c is inconsistent with iii
- c is inconsistent with iv
- c is inconsistent with v
Consistency
- a is consistent with i
- a is consistent with ii
- a is consistent with iii
- a is consistent with v
- b is consistent with i
- b is consistent with ii
- b is consistent with iii
- b is consistent with iv
- b is consistent with v
- d is consistent with i
- d is consistent with ii
- d is consistent with iii
- d is consistent with iv
- d is consistent with v
- e is consistent with i
- e is consistent with ii
- e is consistent with iii
- e is consistent with iv
- e is consistent with v
|
|
Implication
- a implies i
- a implies ii
- a implies iii
- b implies i
- c implies i
- c implies ii
- c implies iii
- c implies iv
- c implies v
- d implies i
- e implies i
- e implies v
Equivalence
- a is equivalent to iii
- b is equivalent to i
- d is equivalent to i
|
2a. A is inconsistent with B.
2b. C is consistent with D.
2c. E is self-inconsistent.
3a. Inconsistency is a modal relation: it has to do with
the way in which the truth-values of a pair of propositions are distributed
across the members of the sets of all possible worlds. It is not a feature
that is restricted to (or unique to) the actual world.
3b. Implication is a modal relation: it has to do with
the way in which the truth-values of a pair of propositions are distributed
across the members of the sets of all possible worlds. It is not a feature
that is restricted to (or unique to) any particular world (e.g. to the world
described in Time Enough for Love).
|