The process of varying the FREQUENCY of a signal, often PERIODICally. An example of FM is the violinist's VIBRATO, where the length of a string (and therefore the resulting pitch) is rapidly altered by a fast oscillating movement of the finger and wrist.
In radio TRANSMISSION, the process involves the MODULATION of a CARRIER wave's frequency by the program signal being transmitted.
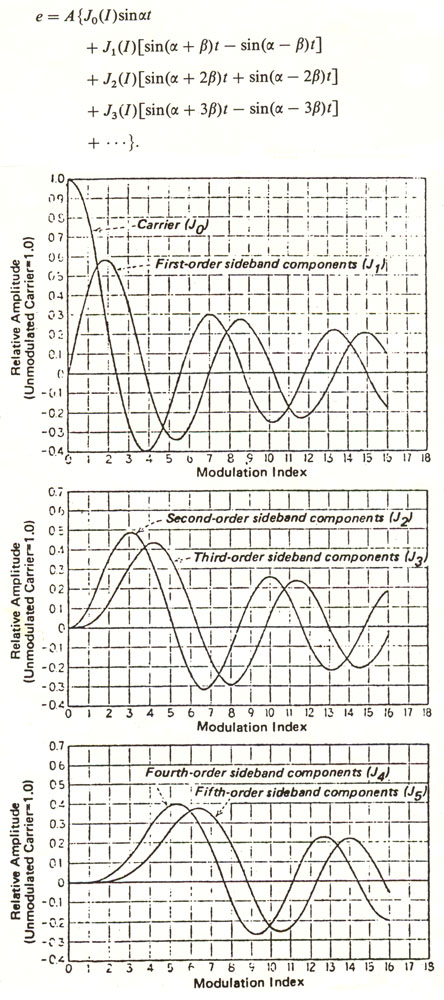
By analogy to the radio sense of the term, frequency modulation is used in electronic and computer SOUND SYNTHESIS to refer to a similar process where both the carrier and modulating signals are in the audio range, or the latter in the SUBAUDIO range. If both are pure SINE TONEs, then the SPECTRUM produced consists of the carrier frequency c plus pairs of SIDEBANDs equally spaced about the carrier at a frequency distance equal to the modulating frequency m. The spectrum may then be described as:
In this expression, the + indicates the upper
sidebands, and the - indicates lower ones, which if producing a
negative frequency appear as a positive frequency component with a PHASE
SHIFT of 180°.
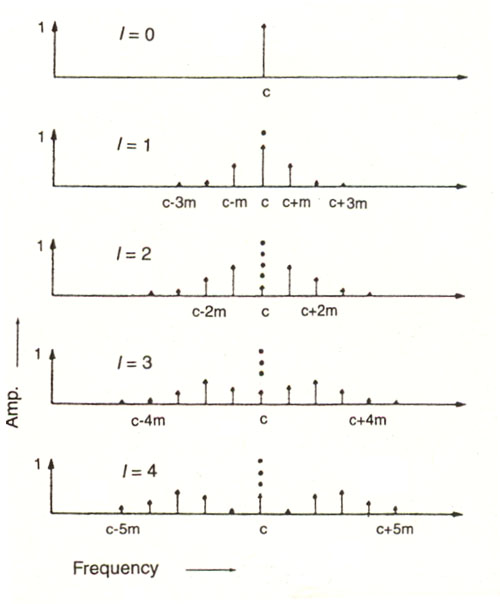
If the modulating signal is 8 Hz or lower, the result of the modulation is a vibrato, whereas above about 20 Hz, the TIMBRE of the tone is changed. In between these two frequencies, a transition from one effect to the other occurs. If the carrier consists of other PARTIALs, then pairs of sidebands are produced about each of them, creating a much more complex spectrum. Generally, the process is used for timbral synthesis.
The strength of the sidebands depends on the MODULATION
INDEX,
which is the ratio of the amplitude to the frequency of the modulating
signal. (Note that the amplitude of the modulating signal equals the
maximum frequency deviation Df of the resulting wave.) That is, the stronger the
amplitude of the modulating signal, the greater the number of sidebands
which contribute significantly to the spectrum. Mathematically, the
amplitude of the nth sideband is given by the nth order Bessel function
for the given modulation index.
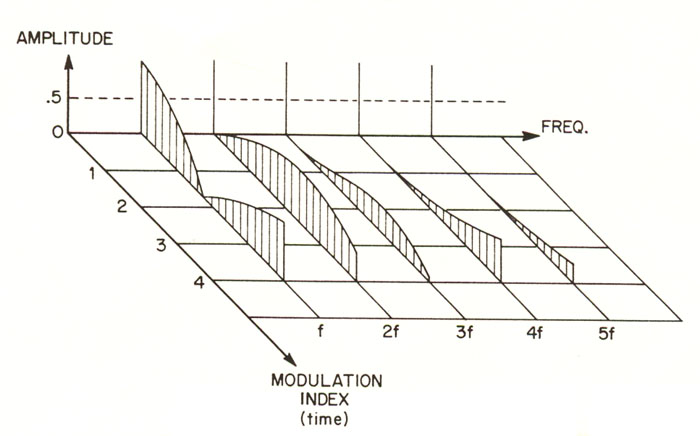
Time-dependent spectra may be produced by varying
the modulation index during the course of the sound. Most
percussion-like sounds are characterized by a strong spectrum activated
during the ATTACK,
which then dies away during the DECAY; this may
be approximated by a sharp rise in the modulation
index followed by a slower decay. The time behaviour of the index,
therefore, controls the spectral envelope of the sound (see SPECTRUM).
Growth of the spectrum
(i.e. number of sidebands) with modulation index
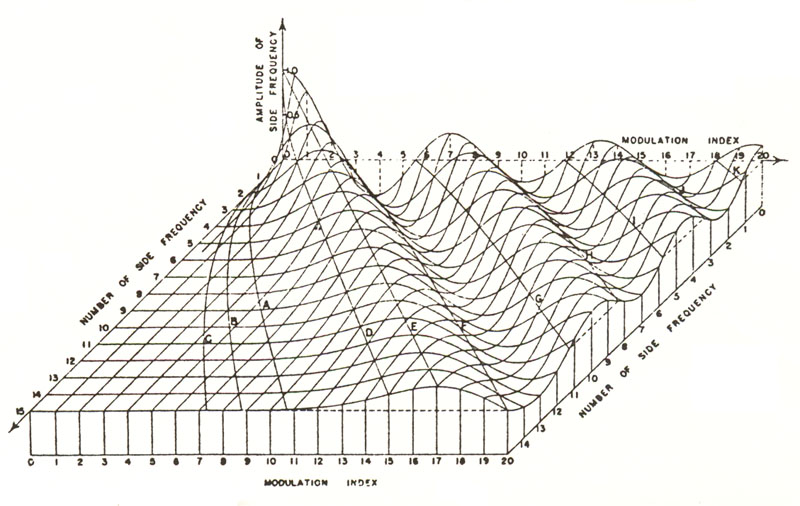
Bessel functions (0 -
5) with increasing modulation index
References:
John Chowning, "The Synthesis of Complex Audio
Spectra by Means of Frequency Modulation," Journal of the Audio
Engineering Society, vol. 21, pp. 526-34, 1973.
Barry Truax, "Organizational Techniques for C:M Ratios in Frequency
Modulation," Computer Music Journal,
1(4), 1977.
Bill Schottstaedt, "The Simulation of Natural Instrument Tones Using
Frequency Modulation with a Complex Modulating Wave," Computer Music Journal, 1(4), 1977.
John Chowning, "Computer Synthesis of the Singing Voice," Proceedings, International
Conference on Music and Technology, Melbourne, 1981.
John Bate, "The Effects of Modulator Phase on Timbres in FM Synthesis,"
Computer
Music Journal, 14(3), 1990.
Frode Holm, "Understanding FM Implementations: A Call for Common
Standards," Computer
Music Journal, 16(1), 1992.

Three examples of frequency modulated signals, where (A) the carrier frequency is higher than the modulating frequency (c:m = 10:1), (B) both frequencies are equal, and (C), the modulating frequency is higher than the carrier (c:m = 1:10). The graph below each modulated signal shows the instantaneous frequency during the course of the modulation. Negative frequencies as shown may be considered as equivalent to positive frequencies with a phase shift of 180°.
For a more detailed account of the properties of FM spectra, consult the FM Tutorial.