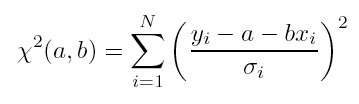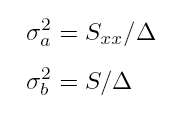Linear Least Squares
If you have a set of data points xi,
and yi, each
with errors sigma-i, which you believe should fit a straight line with
a nonzero x intercept and a nonzero slope then you can get estimates of
the intercept and slope by using the method of least squares--also
known as linear regression or the method of maximum liklihood.
The assummed equation which models the functional relationship of x and y is given by
y = a
+ bx
For the model x and y are considered variables. But in
the process of fitting the experimental points xi and yi are
fixed whereas a and b are varied until the best
match between the experimental points and the data is found. The
"goodness of fit" is definied as the sum of all the squares of the
distances between the experimental points and the line, measured
vertically. This parameter is often called "chi-squared" for
reasons best known to statisticians:
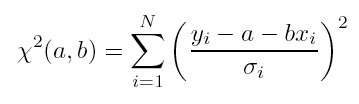
The description of how to minimize chi-squared can be found in many
books, for example "Numerical Recipes" , Lyons, or Bevington's "Data
Analysis...".
The best values of a and b depend on quantities which are sums derived from the data
defined as follows:

The values of a and b are then given by

The errors of a and b are
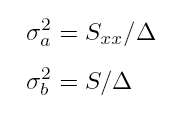
Here is an example of a spreadsheet for a simple case of four data points which fit exactly a line with intercept 10 and slope 1.
You may download the Excel spreadsheet so that you can play with the values and see how it works.
(Those of you with fancy calculators like the TI-83, might enjoy spending a few hours getting this to work on your calculator!)
Source: Numerical Recipes in C, Ch. 15.2 (http://www.nrbook.com/b/bookcpdf/c15-2.pdf)
N. Alberding, May 2003
Created using Mozilla composer and BBEdit Lite. Best viewed with any Browser.