Generalized Durbin-Watson Tests

The AUTOREG Procedure

Generalized Durbin-Watson Tests

Consider the following linear regression model:

$Y={X{\beta}}+{{\nu}}$

where X is an N*k data matrix, ${{\beta}}$ is a k*1 coefficient vector, and ${{\nu}}$ is a N*1 disturbance vector. The error term ${{\nu}}$ is assumed to be generated by the jth order autoregressive process ${{\nu}}$ _t= ${\epsilon}$ _t- ${\varphi}$ _j ${{\nu}}$ _t-j where ${{| {\varphi}_{j}|} \lt 1}$ , ${{\epsilon}_{t}}$ is a sequence of independent normal error terms with mean 0 and variance ${{\sigma}}$ ². Usually, the Durbin-Watson statistic is used to test the null hypothesis ${H_{0}: {\varphi}_{1}=0}$ against ${H_{1}: - {\varphi}_{1}\gt}$ . Vinod (1973) generalized the Durbin-Watson statistic:

$d_{j}=\frac{\sum_{t=j+1}^N{(\hat{{\nu}}_{t}-\hat{{\nu}}_{t-j})^2 }}{\sum_{t=1}^N{\hat{{\nu}}_{t}^2} }$

where $\hat{\nu}$ are OLS residuals. Using the matrix notation,

$d_{j}=\frac{{{\nu}}'M{A}_{j}' A_{j}M{{\nu}}} {{{\nu}}'M{{\nu}}}$

where M = I_N-X(X'X)^-1X' and A_j is a (N-j) ×N matrix:

$A_{j} = [ \matrix{ -1 & 0 & { ... } & 0 & 1 & 0 & { ... } & 0 \cr 0 & -1 & 0 &... ...ots} & {\vdots} & {\vdots} \cr 0 & { ... } & 0 & -1 & 0 & { ... } & 0 & 1} ]$

and there are j-1 zeros between -1 and 1 in each row of matrix A_j.

The QR factorization of the design matrix X yields a N*N orthogonal matrix Q

X = QR

where R is a N*k upper triangular matrix. There exists a N*(N-k) submatrix of Q such that Q₁Q₁' = M and Q₁'Q₁ = I_N-k. Consequently, the generalized Durbin-Watson statistic is stated as a ratio of two quadratic forms:

$d_{j}=\frac{\sum_{l=1}^n{{\lambda}_{jl} {\xi}_{l}}^2}{\sum_{l=1}^n{{\xi}_{l}^2}}$

where ${{\lambda}_{j1}{ ... }{\lambda}_{jn}}$ are upper n eigenvalues of MA_j'A_jM and ${ {\xi}_{l}}$ is a standard normal variate, and n = min(N-k, N-j). These eigenvalues are obtained by a singular value decomposition of Q₁'A_j' (Golub and Loan 1989; Savin and White 1978).

The marginal probability (or p-value) for d_j given c₀ is

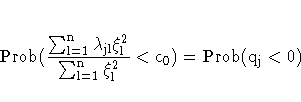
$\rm{Prob}(\frac{\sum_{l=1}^n{{\lambda}_{jl} {\xi}_{l}^2}}{\sum_{l=1}^n{{\xi}_{l}^2}} \lt c_{0})=\rm{Prob}(q_{j} \lt 0)$

where

$q_{j}=\sum_{l=1}^n{( {\lambda}_{jl}-c_{0}) {\xi}_{l}^2}$

When the null hypothesis ${H_{0}: {\varphi}_{j}=0}$ holds, the quadratic form q_j has the characteristic function

${\phi}_{j}(t)={\prod_{l=1}^n (1-2( {\lambda}_{jl}-c_{0})it)^{-1/2}}$

The distribution function is uniquely determined by this characteristic function:

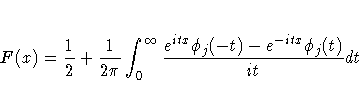
$F(x) = \frac{1}2 + \frac{1}{2{\pi}}\int_{0}^{{\infty}}{\frac{e^{itx}{\phi}_{j}(-t)- e^{-itx}{\phi}_{j}(t)}{it}dt}$

For example, to test ${H_{0}: {\varphi}_{4}=0}$ given ${{\varphi}_{1}={\varphi}_{2}={\varphi}_{3}=0}$ against ${H_{1}: - {\varphi}_{4}\gt}$ , the marginal probability (p-value) can be used:

$F(0) = \frac{1}2 + \frac{1}{2{\pi}}\int_{0}^{{\infty}}{\frac{\ssbeleven ({\phi}_{4}(-t)-{\phi}_{4}(t))} {it}dt}$

where

${\phi}_{4}(t) = {\prod_{l=1}^n (1-2({\lambda}_{4{l}}-\hat{d}_{4})it )^{-1/2}}$

and ${ \hat{d}_{4}}$ is the calculated value of the fourth-order Durbin-Watson statistic.

In the Durbin-Watson test, the marginal probability indicates positive autocorrelation ( ${-{\varphi}_{j}\gt}$ ) if it is less than the level of significance ( ${\alpha}$ ), while you can conclude that a negative autocorrelation ( ${-{\varphi}_{j}\lt}$ ) exists if the marginal probability based on the computed Durbin-Watson statistic is greater than 1- ${\alpha}$ . Wallis (1972) presented tables for bounds tests of fourth-order autocorrelation and Vinod (1973) has given tables for a five percent significance level for orders two to four. Using the AUTOREG procedure, you can calculate the exact p-values for the general order of Durbin-Watson test statistics. Tests for the absence of autocorrelation of order p can be performed sequentially; at the jth step, test ${H_{0}: {\varphi}_{j}=0}$ given ${ {\varphi}_{1}={ ... } = {\varphi}_{j-1}=0}$ against ${ {\varphi}_{j}{\neq}0}$ . However, the size of the sequential test is not known.

The Durbin-Watson statistic is computed from the OLS residuals, while that of the autoregressive error model uses residuals that are the difference between the predicted values and the actual values. When you use the Durbin-Watson test from the residuals of the autoregressive error model, you must be aware that this test is only an approximation. See "Regression with Autoregressive Errors" earlier in this chapter. If there are missing values, the Durbin-Watson statistic is computed using all the nonmissing values and ignoring the gaps caused by missing residuals. This does not affect the significance level of the resulting test, although the power of the test against certain alternatives may be adversely affected. Savin and White (1978) have examined the use of the Durbin-Watson statistic with missing values.

Tests for Serial Correlation with Lagged Dependent Variables

When regressors contain lagged dependent variables, the Durbin-Watson statistic (d₁) for the first-order autocorrelation is biased toward 2 and has reduced power. Wallis (1972) shows that the bias in the Durbin-Watson statistic (d₄) for the fourth-order autocorrelation is smaller than the bias in d₁ in the presence of a first-order lagged dependent variable. Durbin (1970) proposed two alternative statistics (Durbin h and t) that are asymptotically equivalent. The h statistic is written as

$h = \hat{{\rho}}\sqrt{N / (1-N\hat{V})}$

where ${\hat{{\rho}}=\sum_{t=2}^N{\hat{{\nu}}_{t}\hat{{\nu}}_{t-1}}/\sum_{t=1}^N{\hat{{\nu}}_{t}^2}}$ and $\hat{V}$ is the least-squares variance estimate for the coefficient of the lagged dependent variable. Durbin's t-test consists of regressing the OLS residuals ${\hat{{\nu}}_{t}}$ on explanatory variables and ${\hat{{\nu}}_{t-1}}$ and testing the significance of the estimate for coefficient of ${\hat{{\nu}}_{t-1}}$ .

Inder (1984) shows that the Durbin-Watson test for the absence of first-order autocorrelation is generally more powerful than the h-test in finite samples. Refer to Inder (1986) and King and Wu (1991) for the Durbin-Watson test in the presence of lagged dependent variables.

Chapter Contents
Previous
Next
Top