Kuhn-Tucker Conditions

Nonlinear Optimization Examples

Kuhn-Tucker Conditions

The nonlinear programming (NLP) problem with one objective function f and m constraint functions c_i, which are continuously differentiable, is defined as follows:

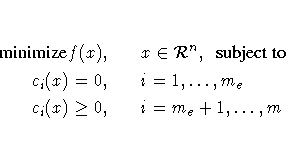
${minimize} f(x), & & x \in {\cal R}^n, \; { subject to} \c_i(x) = 0 , & & i = 1, ... ,m_e \c_i(x) \ge 0 , & & i = m_e+1, ... ,m$

In the preceding notation, n is the dimension of the function f(x), and m_e is the number of equality constraints. The linear combination of objective and constraint functions

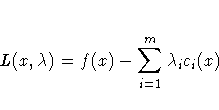
$L(x,\lambda) = f(x) - \sum_{i=1}^m \lambda_i c_i(x)$

is the Lagrange function, and the coefficients $\lambda_i$ are the Lagrange multipliers.

If the functions f and c_i are twice differentiable, the point x^* is an isolated local minimizer of the NLP problem, if there exists a vector $\lambda^*=(\lambda_1^*, ... ,\lambda_m^*)$ that meets the following conditions:

Kuhn-Tucker conditions
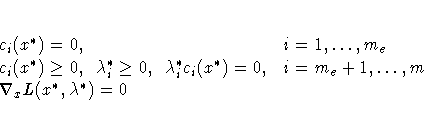
$c_i(x^*) = 0 , & i = 1, ... ,m_e \ c_i(x^*) \ge 0 , \lambda_i^* \ge 0, \lambda_i^* c_i(x^*) = 0 , & i = m_e+1, ... ,m \ \nabla_x L(x^*,\lambda^*) = 0$
Second-order condition
Each nonzero vector $y \in {\cal R}^n$ with
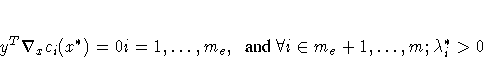
$y^T \nabla_x c_i(x^*) = 0 i = 1, ... ,m_e ,\; { and } \forall i\in {m_e+1, ... ,m}; \lambda_i^* \gt 0$
satisfies
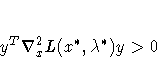
$y^T \nabla_x^2 L(x^*,\lambda^*) y \gt 0$

In practice, you cannot expect that the constraint functions c_i(x^*) will vanish within machine precision, and determining the set of active constraints at the solution x^* may not be simple.

Chapter Contents
Previous
Next
Top