LMS and LTS Calls

Chapter Contents

Language Reference

LMS and LTS Calls

performs robust regression

CALL LMS( sc, coef, wgt, opt, y<, <x><, sorb>>);

robust (resistant) regression method, defined by minimizing the hth ordered squared residual.

CALL LTS( sc, coef, wgt, opt, y<, <x><, sorb>>);

robust (resistant) regression method, defined by minimizing the sum of the h smallest squared residuals.

The Least Median of Squares (LMS) and Least Trimmed Squares (LTS) subroutines perform robust regression (sometimes called resistant regression). They are able to detect outliers and perform a least-squares regression on the remaining observations.

The value of h may be specified, but in most applications the default value works just fine and the results seem to be quite stable toward different choices of h.

The inputs to the LMS and LTS subroutines are as follows:

opt

refers to an options vector with the following components (missing values are treated as default values). The options vector can be a null vector.

opt[1]

specifies whether an intercept is used in the model (opt[1]=0) or not (opt[1] $\neq0$ ). If opt[1]=0, then a column of 1s is added as the last column to the input matrix X; that is, you do not need to add this column of 1s yourself. The default is opt[1]=0.

opt[2]

specifies the amount of printed output. Higher values request additional output and include the output of lower values.

opt[2]=0: prints no output except error messages.
opt[2]=1: prints all output except (1) arrays of O(N), such as weights, residuals, and diagnostics; (2) the history of the optimization process; and (3) subsets that result in singular linear systems.
opt[2]=2: additionally prints arrays of O(N), such as weights, residuals, and diagnostics; also prints the case numbers of the observations in the best subset and some basic history of the optimization process.
opt[2]=3: additionally prints subsets that result in singular linear systems.

The default is opt[2]=0.

opt[3]

specifies whether only LMS or LTS is computed or whether, additionally, least-squares (LS) and weighted least-squares (WLS) regression are computed:

opt[3]=0: computes only LMS or LTS.
opt[3]=1: computes, in addition to LMS or LTS, weighted least-squares regression on the observations with small LMS or LTS residuals (where small is defined by opt[8]).
opt[3]=2: computes, in addition to LMS or LTS, unweighted least-squares regression.
opt[3]=3: adds both unweighted and weighted least-squares regression to LMS and LTS regression.

The default is opt[3]=0.

opt[4]

specifies the quantile h to be minimized. This is used in the objective function. The default is opt[5]= h = [[(N+n+1)/2]], which corresponds to the highest possible breakdown value. This is also the default of the PROGRESS program. The value of h should be in the range $\frac{N}2+1 \leq h \leq \frac{3N}4 + \frac{n+1}4$

opt[5]

specifies the number N_Rep of generated subsets. Each subset consists of n observations (k₁, ... ,k_n), where $1 \leq k_i \leq N$ . The total number of subsets consisting of n observations out of N observations is

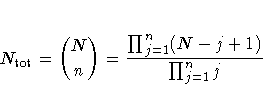
$N_{\rm tot} = {N \choose n} = \frac{\prod_{j=1}^n (N-j+1)} {\prod_{j=1}^n j}$

where n is the number of parameters including the intercept.

Due to computer time restrictions, not all subset combinations of n observations out of N can be inspected for larger values of N and n. Specifying a value of N_Rep < N_tot enables you to save computer time at the expense of computing a suboptimal solution.

If opt[5] is zero or missing, the default number of subsets is taken from the following table.

n	1	2	3	4	5	6	7	8	9	10
N_lower	500	50	22	17	15	14	0	0	0	0
N_upper	1000000	1414	182	71	43	32	27	24	23	22
N_Rep	500	1000	1500	2000	2500	3000	3000	3000	3000	3000

n	11	12	13	14	15
N_lower	0	0	0	0	0
N_upper	22	22	22	23	23
N_Rep	3000	3000	3000	3000	3000

If the number of cases (observations) N is smaller than N_lower, then all possible subsets are used; otherwise, N_Rep subsets are drawn randomly. This means that an exhaustive search is performed for opt[6]=-1. If N is larger than N_upper, a note is printed in the log file indicating how many subsets exist.

opt[7]

specifies that the latest argument sorb contains a given parameter vector b rather than a given subset for which the objective function should be evaluated.

opt[8]

is relevant only for LS and WLS regression (opt[3] > 0). It specifies whether the covariance matrix of parameter estimates and approximate standard errors (ASEs) are computed and printed:

opt[8]=0: does not compute covariance matrix and ASEs.
opt[8]=1: computes the covariance matrix and ASEs but prints only the ASEs.
opt[8]=3: computes and prints both the covariance matrix and the ASEs.

The default is opt[8]=0.

y

refers to an N response vector y.

x

refers to an N ×n matrix X of regressors. If opt[1] is zero or missing, an intercept $x_{n+1} \equiv 1$ is added by default as the last column of X. If the matrix X is not specified, y is analyzed as a univariate data set.

sorb

refers to an n vector containing either of the following:

n observation numbers of a subset for which the objective function should be evaluated; this subset can be the start for a pairwise exchange algorithm if opt[4] is specified.
n given parameters b = (b₁, ... ,b_n) (including the intercept, if necessary) for which the objective function should be evaluated.

Missing values are not permitted in x or y. Missing values in opt cause the default value to be used.

The LMS and LTS subroutines return the following values:

sc

is a column vector containing the following scalar information, where rows 1 -9 correspond to LMS or LTS regression and rows 11 -14 correspond to either LS or WLS:

sc[1]: the quantile h used in the objective function
sc[2]: number of subsets generated
sc[3]: number of subsets with singular linear systems
sc[4]: number of nonzero weights w_i
sc[5]: lowest value of the objective function F_LMS or F_LTS attained
sc[6]: preliminary LMS or LTS scale estimate S_P
sc[7]: final LMS or LTS scale estimate S_F
sc[8]: robust R² (coefficient of determination)
sc[9]: asymptotic consistency factor

If opt[3] > 0, then the following can also be set:

sc[11]: LS or WLS objective function (sum of squared residuals)
sc[12]: LS or WLS scale estimate
sc[13]: R² value for LS or WLS
sc[14]: F value for LS or WLS

For opt[3]=1 or opt[3]=3, these rows correspond to WLS estimates; for opt[3]=2, these rows correspond to LS estimates.

coef

is a matrix with n columns containing the following results in its rows:

coef[1,]: LMS or LTS parameter estimates
coef[2,]: indices of observations in the best subset

If opt[3] > 0, then the following can also be set:

coef[3]: LS or WLS parameter estimates
coef[4]: approximate standard errors of LS or WLS estimates
coef[5]: t-values
coef[6]: p-values
coef[7]: lower boundary of Wald confidence intervals
coef[8]: upper boundary of Wald confidence intervals

For opt[3]=1 or opt[3]=3, these rows correspond to WLS estimates; for opt[3]=2, to LS estimates.

wgt

is a matrix with N columns containing the following results in its rows:

wgt[1]: weights (=1 for small, =0 for large residuals)
wgt[2]: residuals r_i = y_i - x_i b
wgt[3]: resistant diagnostic u_i (note that the resistant diagnostic cannot be computed for a perfect fit when the objective function is zero or nearly zero)

Example

Consider results for Brownlee's (1965) stackloss data. The three explanatory variables correspond to measurements for a plant oxidizing ammonia to nitric acid:

x₁ air flow to the plant
x₂ cooling water inlet temperature
x₃ acid concentration

on 21 consecutive days. The response variable y_i gives the permillage of ammonia lost (stackloss). The data are also given by Rousseeuw & Leroy (1987, p.76) and Osborne (1985, p.267):

 print "Stackloss Data";
 aa = { 1  80  27  89  42,
        1  80  27  88  37,
        1  75  25  90  37,
        1  62  24  87  28,
        1  62  22  87  18,
        1  62  23  87  18,
        1  62  24  93  19,
        1  62  24  93  20,
        1  58  23  87  15,
        1  58  18  80  14,
        1  58  18  89  14,
        1  58  17  88  13,
        1  58  18  82  11,
        1  58  19  93  12,
        1  50  18  89   8,
        1  50  18  86   7,
        1  50  19  72   8,
        1  50  19  79   8,
        1  50  20  80   9,
        1  56  20  82  15,
        1  70  20  91  15 };

Rousseeuw & Leroy (1987, p.76) cite a large number of papers where this data set was analyzed before and state that most researchers "concluded that observations 1, 3, 4, and 21 were outliers," and some people also reported observation 2 as outlier.

For N=21 and n=4 (three explanatory variables including intercept), you obtain a total of 5985 different subsets of 4 observations out of 21. If you decide not to specify optn[5], your LMS and LTS algorithms draw N_rep=2000 random sample subsets. Since there is a large number of subsets with singular linear systems, which you do not want to print, you chose optn[2]=2; for reduced printed output.

  a = aa[,2:4]; b = aa[,5];
  optn = j(8,1,.);
  optn[2]= 2;    /* ipri */
  optn[3]= 3;    /* ilsq */
  optn[8]= 3;    /* icov */

  CALL LMS(sc,coef,wgt,optn,b,a);

   LMS: The 13th ordered squared residual will be minimized.


                 Median and Mean

                       Median              Mean

   VAR1                    58      60.428571429
   VAR2                    20      21.095238095
   VAR3                    87      86.285714286
   Intercep                 1                 1
   Response                15      17.523809524

        Dispersion and Standard Deviation

                   Dispersion            StdDev

   VAR1           5.930408874      9.1682682584
   VAR2           2.965204437       3.160771455
   VAR3          4.4478066555      5.3585712381
   Intercep                 0                 0
   Response       5.930408874      10.171622524

The following are the results of LS regression:

                    Unweighted Least-Squares Estimation


                      LS Parameter Estimates

                         Approx                 Pr >
Variable    Estimate     Std Err    t Value     |t|   

VAR1        0.715640   0.134858     5.31      <.0001    
VAR2        1.295286   0.368024     3.52      0.0026    
VAR3       -0.152123   0.156294    -0.97      0.3440   
Intercep   -39.919674 11.895997    -3.36      0.0038  

Variable    Lower WCI   Upper WCI

VAR1        0.451323  0.979957
VAR2        0.573972  2.016600
VAR3       -0.458453  0.154208
Intercep   -63.2354  -16.603949



                     Sum of Squares = 178.8299616
                       Degrees of Freedom = 17
                    LS Scale Estimate = 3.2433639182

                     Cov Matrix of Parameter Estimates

            VAR1        VAR2         VAR3       Intercep

VAR1        0.018187   -0.036511    0.007144    0.287587
VAR2       -0.036511    0.135442    0.000010   -0.651794
VAR3       -0.007144    0.000011    0.024428   -1.676321
Intercep    0.287587   -0.651794    1.676321  141.514741

                     R-squared = 0.9135769045
                  F(3,17) Statistic = 59.9022259
                    Probability = 3.0163272E-9

These are the LMS results for the 2000 random subsets:

            Random Subsampling for LMS



                                 Best
   Subset    Singular       Criterion     Percent

      500          23        0.163262          25
     1000          55        0.140519          50
     1500          79        0.140519          75
     2000         103        0.126467         100

         Minimum Criterion= 0.1264668282
       Least Median of Squares (LMS) Method
    Minimizing 13th Ordered Squared Residual.
   Highest Possible Breakdown Value =  42.86 %
         Random Selection of 2103 Subsets
       Among 2103 subsets 103 are singular.

            Observations of Best Subset

  15                11                19                10

              Estimated Coefficients

  VAR1              VAR2              VAR3          Intercep

  0.75               0.5                 0            -39.25


          LMS Objective Function = 0.75
           Preliminary LMS Scale = 1.0478510755
                Robust R Squared = 0.96484375
                 Final LMS Scale = 1.2076147288

For LMS observations, 1, 3, 4, and 21 have scaled residuals larger than 2.5 (table not shown) and are considered outliers. These are the corresponding WLS results:

                       Weighted Least-Squares Estimation



                     RLS Parameter Estimates Based on LMS

                            Approx             Pr >
  Variable    Estimate     Std Err  t Value     |t|   

  VAR1        0.797686  0.067439    11.83     <.0001   
  VAR2        0.577340  0.165969     3.48     0.0041   
  VAR3       -0.067060  0.061603    -1.09     0.2961  
  Intercep  -37.652459  4.732051    -7.96     <.0001 


                        Lower WCI   Upper WCI

                        0.665507    0.929864
                        0.252047    0.902634
                       -0.187800    0.053680
                      -46.927108  -28.37781

                   Weighted Sum of Squares = 20.400800254
                          Degrees of Freedom = 13
                     RLS Scale Estimate = 1.2527139846

                   Cov Matrix of Parameter Estimates

              VAR1         VAR2         VAR3         Intercep

   VAR1       0.004548    -0.007921    -0.001199     0.001568
   VAR2      -0.007921     0.027546    -0.000463    -0.065018
   VAR3      -0.001199    -0.000463     0.003795    -0.246102
   Intercep   0.001568    -0.065018    -0.246102    22.392305

                   Weighted R-squared = 0.9750062263
                    F(3,13) Statistic = 169.04317954
                       Probability = 1.158521E-10
                There are 17 points with nonzero weight.
                     Average Weight = 0.8095238095

References

Brownlee, K.A. (1965), Statistical Theory and Methodology in Science and Engineering, New York: John Wiley & Sons, Inc.
Davies, L. (1992), ``The Asymptotics of Rousseeuw's Minimum Volume Ellipsoid Estimator,'' The Annals of Statistics, 20, 1828 -1843.
Rousseeuw, P.J. (1984), "Least Median of Squares Regression," Journal of the American Statistical Association, 79, 871 -880.
Rousseeuw, P.J. (1985), "Multivariate Estimation with High Breakdown Point," in Mathematical Statistics and Applications, ed. by W. Grossmann, G. Pflug, I. Vincze, and W. Wertz, Dordrecht: Reidel Publishing Company, 283 -297.
Rousseeuw, P.J. and Croux, C. (1993), "Alternatives to the Median Absolute Deviation," Journal of the American Statistical Association, 88, 1273 -1283.
Rousseeuw, P.J. and Hubert, M. (1997), "Recent Developments in PROGRESS," in L₁-Statistical Procedures and Related Topics, ed. by Y. Dodge, IMS Lecture Notes - Monograph Series, No. 31, 201 -214.
Rousseeuw, P.J. and Leroy, A.M. (1987), Robust Regression and Outlier Detection, New York: John Wiley & Sons, Inc.
Rousseeuw, P.J. and Van Driessen, K. (1997), ``A fast Algorithm for the Minimum Covariance Determinant Estimator,'' submitted for publication.
Rousseeuw, P.J. and Van Zomeren, B.C. (1990), "Unmasking Multivariate Outliers and Leverage Points," Journal of the American Statistical Association, 85, 633 -639.

Chapter Contents
Previous
Next
Top