ORTVEC Call
provides columnwise orthogonalization by
the Gram-Schmidt process and stepwise QR
decomposition by the Gram-Schmidt process
- CALL ORTVEC( w, r,
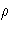 , lindep, v<,
q>);
, lindep, v<,
q>);
The ORTVEC subroutine returns the following values:
- w
- If the Gram-Schmidt process converges (lindep=0), w is
the m ×1 vector w orthonormal to the columns of Q,
which is assumed to have
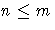 (nearly) orthonormal columns.
If the Gram-Schmidt process does not converge
(lindep=1), w is a vector of missing values.
For stepwise QR decomposition, w is the
(n+1) th orthogonal column of the matrix Q.
If there is no matrix Q, that is, if the q argument is
not specified, w is the normalized value of the vector v,
(nearly) orthonormal columns.
If the Gram-Schmidt process does not converge
(lindep=1), w is a vector of missing values.
For stepwise QR decomposition, w is the
(n+1) th orthogonal column of the matrix Q.
If there is no matrix Q, that is, if the q argument is
not specified, w is the normalized value of the vector v,
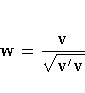
- r
- If the Gram-Schmidt process converges (lindep=0), r
specifies the n ×1 vector r of Fourier coefficients.
If the Gram-Schmidt process does not converge
(lindep=1), r is a vector of missing values.
If the q argument is not specified,
r is a vector with zero dimension.
For stepwise QR decomposition, r contains the n upper
triangular elements of the (n+1) th column of R.
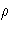
- If the Gram-Schmidt process converges (lindep=0),
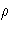 specifies the distance from w to the range of Q.
Even if the Gram-Schmidt process converges, if
specifies the distance from w to the range of Q.
Even if the Gram-Schmidt process converges, if
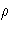 is sufficiently small, the vector v
may be linearly dependent on the columns of Q.
If the Gram-Schmidt process does not converge
(lindep=1),
is sufficiently small, the vector v
may be linearly dependent on the columns of Q.
If the Gram-Schmidt process does not converge
(lindep=1), 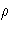 is set to 0.
For stepwise QR decomposition,
is set to 0.
For stepwise QR decomposition, 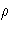 contains the
diagonal element of the (n+1) th column of R.
contains the
diagonal element of the (n+1) th column of R.
- lindep
- returns a value of 1 if the Gram-Schmidt
process does not converge in 10 iterations.
In most cases, if lindep=1, the input vector v is
linearly dependent on the n columns of the input matrix Q.
In that case,
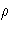 is set to 0, and the
results w and r contain missing values.
If lindep=0, the Gram-Schmidt process did converge,
and the results w, r, and
is set to 0, and the
results w and r contain missing values.
If lindep=0, the Gram-Schmidt process did converge,
and the results w, r, and 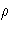 are computed.
are computed.
The inputs to the ORTVEC subroutine are as follows:
- v
- specifies an m ×1 vector v that is
to be orthogonalized to the n columns of Q.
For stepwise QR decomposition of a matrix, v is the
(n+1) th matrix column before its orthogonalization.
- q
- specifies an optional m ×n matrix Q that is
assumed to have
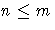 (nearly) orthonormal columns.
Thus, the n ×n matrix Q' Q
should approximate the identity matrix.
The column orthonormality assumption
is not tested in the ORTVEC call.
If it is violated, the results are not predictable.
The argument q can be omitted or can have zero rows and columns.
For stepwise QR decomposition of a matrix, q contains
the first n matrix columns that are already orthogonal.
(nearly) orthonormal columns.
Thus, the n ×n matrix Q' Q
should approximate the identity matrix.
The column orthonormality assumption
is not tested in the ORTVEC call.
If it is violated, the results are not predictable.
The argument q can be omitted or can have zero rows and columns.
For stepwise QR decomposition of a matrix, q contains
the first n matrix columns that are already orthogonal.
The relevant formula for the ORTVEC subroutine is
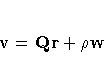
Assuming that the m ×n matrix Q has n
(nearly) orthonormal columns, the ORTVEC subroutine
orthogonalizes the vector v to the columns of Q.
The vector r is the array of Fourier coefficients, and
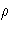 is the distance from w to the range of Q.
is the distance from w to the range of Q.
There are two special cases:
- If m > n, ORTVEC normalizes the result w,
so that w' w = 1.
- If m = n, the output vector w is the null vector.
The case m < n is not possible since Q is
assumed to have n (nearly) orthonormal columns.
To initialize a stepwise QR decomposition, ORTVEC
can be called to normalize v only, that is,
to compute 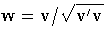 and
and 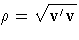 only.
There are two ways of using the ORTVEC call for this reason:
only.
There are two ways of using the ORTVEC call for this reason:
- Omit the last argument q, as in
call ortvec(w,r,rho,lindep,v);.
- Provide a matrix Q with zero rows and columns,
for example, by using the free q; command.
In both cases, r is a column vector with zero rows.
The ORTVEC subroutine is useful for the following applications:
- performing stepwise QR decomposition.
Compute Q and R, so that A = QR,
where Q is column orthonormal, Q' Q = I, and R is upper triangular.
The jth step is applied to the jth column,
v, of A, and it computes the jth column
w of Q and the jth column,
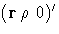 , of R.
, of R.
- computing the m ×(m-n) null space matrix, Q2,
corresponding to an m ×n range space matrix,
Q1 (m>n), by the following stepwise process:
set v = ei (where ei is the ith unit
vector) and try to make it orthogonal to all column
vectors of Q1 and the already generated Q2,
if the subroutine is successful, append w to
Q2; otherwise, try v = ei+1.
The 4 ×3 matrix Q contains the
unit vectors e1, e3, and e4.
The column vector v is pairwise linearly
independent with the three columns of Q.
As expected, the ORTVEC call computes the vector w as
the unit vector e2 with 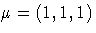 and
and 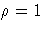 .
.
proc iml;
q = { 1 0 0,
0 0 0,
0 1 0,
0 0 1 };
v = { 1, 1, 1, 1 };
call ortvec(w,u,rho,lindep,v,q);
print rho u w;
You can perform the QR decomposition of the
linearly independent columns of an m ×n
matrix A with the following statements:
proc iml;
a = { . . . enter matrix A here . . . };
nind = 0; ndep = 0; dmax = 0.;
n = ncol(a); m = nrow(a);
free q;
do j = 1 to n;
v = a[ ,j];
call ORTVEC(w,u,rho,lindep,v,q);
aro = abs(rho);
if aro > dmax then dmax = aro;
if aro <= 1.e-10 * dmax then lindep = 1;
if lindep = 0 then do;
nind = nind + 1;
q = q || w;
if nind = n then r = r || (u // rho);
else r = r || (u // rho // j(n-nind,1,0.));
end;
else do;
print "Column " j " is linearly dependent.";
ndep = ndep + 1; ind[ndep] = j;
end;
end;
Next, process the remaining columns of A:
do j = 1 to ndep;
k = ind[ndep-j+1];
v = a[ ,k];
call ORTVEC(w,u,rho,lindep,v,q);
if lindep = 0 then do;
nind = nind + 1;
q = q || w;
if nind = n then r = r || (u // rho);
else r = r || (u // rho // j(n-nind,1,0.));
end;
end;
Now compute the null space in the last columns of Q:
do i = 1 to m;
if nind < m then do;
v = j(m,1,0.); v[i] = 1.;
call ORTVEC(w,u,rho,lindep,v,q);
aro = abs(rho);
if aro > dmax then dmax = aro;
if aro <= 1.e-10 * dmax then lindep = 1;
if lindep = 0 then do;
nind = nind + 1;
q = q || w;
end;
else print "Unit vector" i "linearly dependent.";
end;
end;
if nind < m then do;
print "This is theoretically not possible.";
end;
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
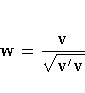
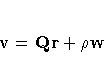
![]() and
and ![]() only.
There are two ways of using the ORTVEC call for this reason:
only.
There are two ways of using the ORTVEC call for this reason:
![]() and
and ![]() .
.