FFT Function

Language Reference

FFT Function

performs the finite Fourier transform

FFT( x)

where x is a 1 ×n or n ×1 numeric vector.

The FFT function returns the cosine and sine coefficients for the expansion of a vector into a sum of cosine and sine functions.

The argument of the FFT function, x, is a 1 ×n or n ×1 vector. The value returned is the resulting transform, an np ×2 matrix, where

np = floor([n/2] + 1 )

The elements of the first column of the returned matrix are the cosine coefficients; that is, the ith element of the first column is

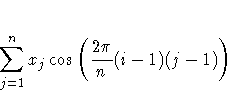
$\sum_{j=1}^n x_j \cos ( \frac{2\pi}n(i-1)(j-1) )$

for i = 1, ... ,np, where the elements of x are denoted as x_j. The elements of the second column of the returned matrix are the sine coefficients; that is, the ith element of the second column is

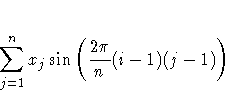
$\sum_{j=1}^n x_j \sin ( \frac{2\pi}n (i-1)(j-1) )$

for i = 1, ... , np.

Note: For most efficient use of the FFT function, n should be a power of 2. If n is a power of 2, a fast Fourier transform is used (Singleton 1969); otherwise, a Chirp-Z algorithm is used (Monro and Branch 1976).

The FFT function can be used to compute the periodogram of a time series. In conjunction with the inverse finite Fourier transform routine IFFT, the FFT function can be used to efficiently compute convolutions of large vectors (Gentleman and Sande 1966; Nussbaumer 1982). An example of a valid statement follows:

   a=fft(c);

Chapter Contents
Previous
Next
Top