Solving a System of Equations

Tutorial: A Module for Linear Regression

Solving a System of Equations

Because IML is built around traditional matrix algebra notation, it is often possible to directly translate mathematical methods from matrix algebraic expressions into executable IML statements. For example, consider the problem of solving three simultaneous equations:

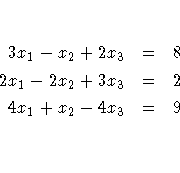
$3x_1 - x_2 + 2x_3 & = & 8 \ 2x_1 - 2x_2 + 3x_3 & = & 2 \4x_1 + x_2 - 4x_3 & = & 9 \$

These equations can be written in matrix form as

$[ 3 & -1 & 2 \ 2 & -2 & 3 \ 4 & 1 & -4 \ ] [ x_1 \ x_2 \ x_3 \ ] = [ 8 \ 2 \ 9 \ ]$

and can be expressed symbolically as

Ax = c

Because A is nonsingular, the system has a solution given by

x = A^-1c

In the following example, you solve this system of equations using an interactive session. Submit the PROC IML statement to begin the procedure. Throughout this chapter, the right angle brackets (>) indicate statements you submit; responses from IML follow:

   > proc iml;

   IML Ready

Enter

   > reset print;

The PRINT option of the RESET command causes automatic printing of results. Notice that as you submit each statement, it is executed and the results are displayed. While you are learning IML or developing modules, it is a good idea to have all results printed automatically. Once you are familiar with SAS/IML software, you will not need to use automatic printing.

Next, set up the matrices A and c. Both of these matrices are input as matrix literals; that is, input the row and column values as discussed in Chapter 2, "Understanding the Language."

   > a={3  -1  2,
   >    2  -2  3,
   >    4   1 -4};

               A             3 rows      3 cols    (numeric)

                                3        -1         2
                                2        -2         3
                                4         1        -4

   > c={8, 2, 9};

                C             3 rows      1 col     (numeric)

                                          8
                                          2
                                          9

Now write the solution equation, x = A^-1c, as an IML statement. The appropriate statement is an assignment statement that uses a built-in function and an operator (INV is a built-in function that takes the inverse of a square matrix, and * is the operator for matrix multiplication).

   > x=inv(a)*c;

              X             3 rows      1 col     (numeric)

                                          3
                                          5
                                          2

After IML executes the statement, the first row of matrix X contains the x₁ value for which you are solving, the second row contains the x₂ value, and the third row contains the x₃ value.

Now end the session by entering the QUIT command.

   >   quit;

       Exiting IML

Chapter Contents
Previous
Next
Top