Example 8.11: Regression Quantiles

General Statistics Examples

Example 8.11: Regression Quantiles

The technique of parameter estimation in linear models using the notion of regression quantiles is a generalization of the LAE or LAV least absolute value estimation technique. For a given quantile q, the estimate b^* of ${\beta}$ in the model

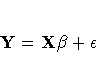
$Y=X{\beta} + {\epsilon}$

is the value of b that minimizes

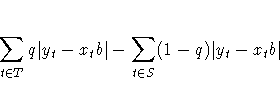
$\sum_{t \in T} q| y_t - x_t b| - \sum_{t \in S} (1-q) | y_t - x_t b|$

where $T=\{t| y_t \geq x_t b\}$ and $S=\{t| y_t \leq x_t\}$ .For q=0.5, the solution b^* is identical to the estimates produced by the LAE. The following routine finds this estimate using linear programming:

      /* Routine to find Regression Quantiles                   */
      /* yname:   name of dependent variable                    */
      /* y:       dependent variable                            */
      /* xname:   names of independent variables                */
      /* X:       independent variables                         */
      /* b:       estimates                                     */
      /* predict: predicted values                              */
      /* error:   difference of y and predicted                 */
      /* q:       quantile                                      */
      /*                                                        */
      /* notes: This subroutine finds the estimates b           */
      /* that minimize                                          */
      /*                                                        */
      /* q * (y - Xb) * e - (1-q) * (Xb - y) * ^e               */
      /*                                                        */
      /* where e = ( Xb <= y ). When q = .5 this is equivalent  */
      /* to minimizing the sum of the absolute deviations.      */
      /*                                                        */
      /* This subroutine follows the approach given in:         */
      /*                                                        */
      /* Koenker, R. and G. Bassett (1978)                      */
      /*                                                        */
      /* Bassett, G. and R. Koenker (1982).                     */
      /*                                                        */
   start rq(yname,y,xname,x,b,predict,error,q);
      bound=1.0e10;
      coef=x`;
      m=nrow(coef);
      n=ncol(coef);

         /* Build rhs and bounds */
      r=repeat(0,m+2,1);
      L=repeat(q-1,1,n)||repeat(0,1,m)||-bound||-bound;
      u=repeat(q,1,n)||repeat(.,1,m)||{ . . };

         /* Build coefficient matrix and basis */

      a=(y`||repeat(0,1,m)||{ -1 0 })//
        (repeat(0,1,n)||repeat(-1,1,m)||{ 0 -1 })//
        (coef||I(m)||repeat(0,m,2));
      basis=n+m+2-(0:n+m+1);

         /* Find a feasible solution */
      call lp(rc,p,d,a,r,,u,L,basis);

         /* Find the optimal solution */
      L=repeat(q-1,1,n)||repeat(0,1,m)||-bound||{0};
      u=repeat(q,1,n)||repeat(0,1,m)||{ . 0 };
      call lp(rc,p,d,a,r,n+m+1,u,L,basis);

         /* Report the solution */
      variable=xname`;
      b=d[3:m+2];
      predict=X*b;
      error=y-predict;
      wsum=sum(choose(error<0,(q-1)*error,q*error));
      print ,,'Regression Quantile Estimation' ,
              'Dependent Variable: ' yname ,
              'Regression Quantile: ' q ,
              'Number of Observations: ' n ,
              'Sum of Weighted Absolute Errors: ' wsum ,
               variable b,
               X y predict error;
   finish rq;

The following example uses data on the United States population from 1790 to 1970:

   z = { 3.929 1790 ,
         5.308 1800 ,
         7.239 1810 ,
         9.638 1820 ,
        12.866 1830 ,
        17.069 1840 ,
        23.191 1850 ,
        31.443 1860 ,
        39.818 1870 ,
        50.155 1880 ,
        62.947 1890 ,
        75.994 1900 ,
        91.972 1910 ,
       105.710 1920 ,
       122.775 1930 ,
       131.669 1940 ,
       151.325 1950 ,
       179.323 1960 ,
       203.211 1970 };

   y=z[,1];
   x=repeat(1,19,1)||z[,2]||z[,2]##2;
   run rq('pop',y,{'intercpt' 'year' 'yearsq'},x,b1,pred,resid,.5);

The output is shown below.

Dependent Variable:	pop

	Q
Regression Quantile:	0.5

	N
Number of Observations:	19

	WSUM
Sum of Weighted Absolute Errors:	14.826429

VARIABLE	B
intercpt	21132.758
year	-23.52574
yearsq	0.006549

X			Y	PREDICT	ERROR
1	1790	3204100	3.929	5.4549176	-1.525918
1	1800	3240000	5.308	5.308	-4.54E-12
1	1810	3276100	7.239	6.4708902	0.7681098
1	1820	3312400	9.638	8.9435882	0.6944118
1	1830	3348900	12.866	12.726094	0.1399059
1	1840	3385600	17.069	17.818408	-0.749408
1	1850	3422500	23.191	24.220529	-1.029529
1	1860	3459600	31.443	31.932459	-0.489459
1	1870	3496900	39.818	40.954196	-1.136196
1	1880	3534400	50.155	51.285741	-1.130741
1	1890	3572100	62.947	62.927094	0.0199059
1	1900	3610000	75.994	75.878255	0.1157451
1	1910	3648100	91.972	90.139224	1.8327765
1	1920	3686400	105.71	105.71	8.669E-13
1	1930	3724900	122.775	122.59058	0.1844157
1	1940	3763600	131.669	140.78098	-9.111976
1	1950	3802500	151.325	160.28118	-8.956176
1	1960	3841600	179.323	181.09118	-1.768184
1	1970	3880900	203.211	203.211	-2.96E-12

The L1 norm (when q=0.5) tends to allow the fit to be better at more points at the expense of allowing some points to fit worse, as the plot of the residuals against the least squares residuals:

      /* Compare L1 residuals with least squares residuals  */
      /* Compute the least squares residuals                */
   resid2=y-x*inv(x`*x)*x`*y;

      /* x axis of plot */
   xx=repeat(x[,2] ,3,1);

      /* y axis of plot */
   yy=resid//resid2//repeat(0,19,1);

      /* plot character*/
   id=repeat('1',19,1)//repeat('2',19,1)//repeat('-',19,1);
   call pgraf(xx||yy,id,'Year','Residual',
              '1=L(1) residuals, 2=least squares residual');

The output generated is shown below.

                                                                                
                                                                                
                                                                                
                  1=l(1) residuals, 2=least squares residual                    
                                                                        
        |                                                                        
      5 +    
        |                                              2                    2      
R       |                                                     2                   
e       |           1  1                        2  2   1  2             2              
s     0 +    -  1   -  -   1  -   -  1   -  2   1  1   -  1   1  -   -  -   1                                                                     
i       |    1                1   1      1  1                           1              
d       |                                                                       
u       |
a    -5 +                                                        2   2           
l       |                                                                        
        |                                                                        
        |                                                        1   1                                                                                    
    -10 +                                                                              
        |                                                                        
        -+------+------+------+------+------+------+------+------+------+------+-
       1780   1800   1820   1840   1860   1880   1900   1920   1940   1960   1980
                                                                                
                                           Year

Chapter Contents
Previous
Next
Top