Example 8.2: Newton's Method for Solving Nonlinear Systems of Equations

Chapter Contents

General Statistics Examples

Example 8.2: Newton's Method for Solving Nonlinear Systems of Equations

This example solves a nonlinear system of equations by Newton's method. Let the nonlinear system be represented by

F(x) = 0

where x is a vector and F is a vector-valued, possibly nonlinear, function.

In order to find x such that F goes to 0, an initial estimate x₀ is chosen, and Newton's iterative method for converging to the solution is used:

x_n+1 = x_n - J^-1(x_n) F(x_n)

where J(x) is the Jacobian matrix of partial derivatives of F with respect to x.

For optimization problems, the same method is used, where F(x) is the gradient of the objective function and J(x) becomes the Hessian (Newton-Raphson).

In this example, the system to be solved is

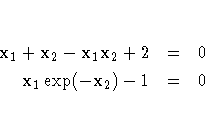
$x_1 + x_2 - x_1{x}_2 + 2 & = & 0 \x_1 \exp(-x_2) - 1 & = & 0$

The code is organized into three modules: NEWTON, FUN, and DERIV.

      /*     Newton's Method to Solve a Nonlinear Function      */
      /* The user must supply initial values,                   */
      /* and the FUN and DERIV functions.                       */
      /* on entry: FUN evaluates the function f in terms of x   */
      /* initial values are given to x                          */
      /* DERIV evaluates jacobian j                             */
      /* tuning variables: CONVERGE, MAXITER.                   */
      /* on exit: solution in x, function value in f close to 0 */
      /* ITER has number of iterations.                         */

   start newton;
      run fun;          /* evaluate function at starting values */
      do iter=1 to maxiter  /* iterate until maxiter iterations */
      while(max(abs(f))>converge);            /* or convergence */
         run deriv;                /* evaluate derivatives in j */
         delta=-solve(j,f);      /* solve for correction vector */
         x=x+delta;                    /* the new approximation */
         run fun;                      /* evaluate the function */
      end;
   finish newton;

   maxiter=15;                    /* default maximum iterations */
   converge=.000001;           /* default convergence criterion */


      /* User-supplied function evaluation */
   start fun;
      x1=x[1] ;
      x2=x[2] ;                           /* extract the values */
      f= (x1+x2-x1*x2+2)//
      (x1*exp(-x2)-1);                 /* evaluate the function */
   finish fun;

      /* User-supplied derivatives of the function */
   start deriv;
      /* evaluate jacobian */
      j=((1-x2)||(1-x1) )//(exp(-x2)||(-x1*exp(-x2)));
   finish deriv;

   do;
      print "Solving the system: X1+X2-X1*X2+2=0, X1*EXP(-X2)-1=0" ,;
      x={.1, -2};     /* starting values */
      run newton;
      print x f;
   end;

The results are shown below.

The SAS System

Solving the system: X1+X2-X1X2+2=0, X1EXP(-X2)-1=0

X	F
0.0977731	5.3523E-9
-2.325106	6.1501E-8

Chapter Contents
Previous
Next
Top