Example 9.5: MVE: Stackloss Data

Robust Regression Examples

Example 9.5: MVE: Stackloss Data

This example analyzes the three regressors of Brownlee's (1965) stackloss data. By default, the MVE subroutine, like the MINVOL subroutine, tries only 2000 randomly selected subsets in its search. There are, in total, 5985 subsets of 4 cases out of 21 cases.

   title2 "***MVE for Stackloss Data***";
   title3 "*** Use All Subsets***";
      a = aa[,2:4];
      optn = j(8,1,.);
      optn[1]= 2;              /* ipri */
      optn[2]= 1;              /* pcov: print COV */
      optn[3]= 1;              /* pcor: print CORR */
      optn[6]= -1;             /* nrep: use all subsets */
   call mve(sc,xmve,dist,optn,a);

The first part of the output shows the classical scatter and correlation matrix.

Output 9.5.1: Some Simple Statistics

Minimum Volume Ellipsoid (MVE) Estimation

Consider Ellipsoids Containing 12 Cases.

Classical Covariance Matrix
	VAR1	VAR2	VAR3
VAR1	84.057142857	22.657142857	24.571428571
VAR2	22.657142857	9.9904761905	6.6214285714
VAR3	24.571428571	6.6214285714	28.714285714

Classical Correlation Matrix
	VAR1	VAR2	VAR3
VAR1	1	0.781852333	0.5001428749
VAR2	0.781852333	1	0.3909395378
VAR3	0.5001428749	0.3909395378	1

Classical Mean
VAR1	60.428571429
VAR2	21.095238095
VAR3	86.285714286

The second part of the output shows the results of the optimization (complete subset sampling).

Output 9.5.2: Iteration History

Random Subsampling for MVE

Subset	Singular	Best Criterion	Percent
500	23	165.830053	25
1000	55	165.634363	50
1500	79	165.634363	75
2000	103	165.634363	100

Minimum Criterion= 165.63436284

Among 2103 subsets 103 are singular.

Observations of Best Subset
14	20	7	10

Initial MVE Location Estimates
VAR1	58.5
VAR2	20.25
VAR3	87

Initial MVE Scatter Matrix
	VAR1	VAR2	VAR3
VAR1	34.829014749	28.413143611	62.32560534
VAR2	28.413143611	38.036950318	58.659393261
VAR3	62.32560534	58.659393261	267.63348175

The third part of the output shows the optimization results after local improvement.

Output 9.5.3: Table of MVE Results

Final MVE Estimates (Using Local Improvement)

Number of Points with Nonzero Weight=17

Robust MVE Location Estimates
VAR1	56.705882353
VAR2	20.235294118
VAR3	85.529411765

Robust MVE Scatter Matrix
	VAR1	VAR2	VAR3
VAR1	23.470588235	7.5735294118	16.102941176
VAR2	7.5735294118	6.3161764706	5.3676470588
VAR3	16.102941176	5.3676470588	32.389705882

Eigenvalues of Robust Scatter Matrix
VAR1	46.597431018
VAR2	12.155938483
VAR3	3.423101087

Robust Correlation Matrix
	VAR1	VAR2	VAR3
VAR1	1	0.6220269501	0.5840361335
VAR2	0.6220269501	1	0.375278187
VAR3	0.5840361335	0.375278187	1

The final output presents a table containing the classical Mahalanobis distances, the robust distances, and the weights identifying the outlying observations (that is, the leverage points when explaining y with these three regressor variables).

Output 9.5.4: Mahalanobis and Robust Distances

Classical Distances and Robust (Rousseeuw) Distances
Unsquared Mahalanobis Distance and
Unsquared Rousseeuw Distance of Each Observation
N	Mahalanobis Distances	Robust Distances	Weight
1	2.253603	5.528395	0
2	2.324745	5.637357	0
3	1.593712	4.197235	0
4	1.271898	1.588734	1.000000
5	0.303357	1.189335	1.000000
6	0.772895	1.308038	1.000000
7	1.852661	1.715924	1.000000
8	1.852661	1.715924	1.000000
9	1.360622	1.226680	1.000000
10	1.745997	1.936256	1.000000
11	1.465702	1.493509	1.000000
12	1.841504	1.913079	1.000000
13	1.482649	1.659943	1.000000
14	1.778785	1.689210	1.000000
15	1.690241	2.230109	1.000000
16	1.291934	1.767582	1.000000
17	2.700016	2.431021	1.000000
18	1.503155	1.523316	1.000000
19	1.593221	1.710165	1.000000
20	0.807054	0.675124	1.000000
21	2.176761	3.657281	0

Distribution of Robust Distances

MinRes	1st Qu.	Median	Mean	3rd Qu.	MaxRes
0.6751244996	1.5084120761	1.7159242054	2.2282960174	2.0831826658	5.6373573538

Cutoff Value = 3.0575159206

The cutoff value is the square root of the 0.975 quantile of the chi square distribution
with 3 degrees of freedom.

There are 4 points with large robust distances receiving zero weights. These may include
boundary cases. Only points whose robust distances are subs tantially larger than the
cutoff value should be considered outliers.

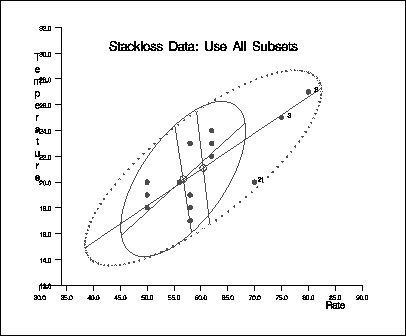
The following specification generates three bivariate plots of the classical and robust tolerance ellipsoids, one plot for each pair of variables:

      optn = j(8,1,.); optn[6]= -1;
      vnam = { "Rate", "Temperature", "AcidConcent" };
      filn = "stl";
      titl = "Stackloss Data: Use All Subsets";
   call scatmve(2,optn,.9,a,vnam,titl,1,filn);

The output follows.

Output 9.5.5: Stackloss Data: Rate vs. Temperature

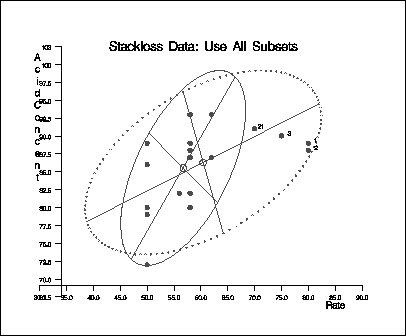
Output 9.5.6: Stackloss Data: Rate vs. Acid Concent

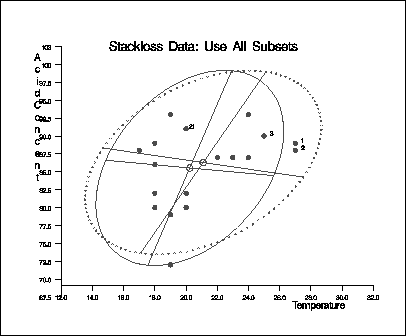
Output 9.5.7: Stackloss Data: Temperature vs. Acid Concent

Chapter Contents
Previous
Next
Top