Anscombe Residuals
For nonnormal response distributions in
generalized linear models, the distribution
of the Pearson residuals is often skewed.
Anscombe proposed a residual using a function
A(y) in place of y in the residual
derivation (Anscombe 1953, McCullagh and Nelder 1989).
The function A(y) is chosen to make the distribution
of A(y) as normal as possible and is given by

where V(t) is the variance function.
For a binomial distribution with mi
trials in the ith observation,
the Anscombe residual is defined as

For other distributions, the Anscombe residual is defined as

where 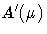 is the derivative of
is the derivative of 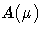 .
.
For the response distributions used in the fit analysis,
Anscombe residuals are
- Normal
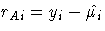
- Inverse Gaussian
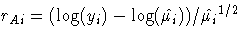
- Gamma
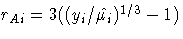
- Poisson
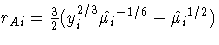
- Binomial

where 
You can save Anscombe residuals to your data set by using the
Output Variables dialog, as shown in Figure 39.5,
or the Vars menu, as shown in Figure 39.48.
These residuals are stored in variables named
RA_yname for each response variable,
where yname is the response variable name.
The standardized and studentized Anscombe residuals are


where 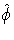 is the
estimate of the dispersion parameter
is the
estimate of the dispersion parameter 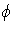 , and
, and
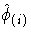 is a one-step approximation of
is a one-step approximation of 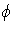 after
excluding the ith observation.
after
excluding the ith observation.
The standardized Anscombe residuals are stored
in variables named RAS_yname and the studentized
Anscombe residuals are stored in variables named
RAT_yname for each response variable,
where yname is the response variable name.
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.




