Specialized Capability Indices

PROC CAPABILITY and General Statements

Specialized Capability Indices

This section describes a number of specialized capability indices which you can request with the SPECIALINDICES option in the PROC CAPABILITY statement.

The Index k

The process capability index k (also denoted by K) is computed as

$k = \frac{2 | m - \bar{X}|}{{USL} - {LSL}}$

where m = (1/2)(USL + LSL) is the midpoint of the specification limits, 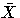$\bar{X}$ is the sample mean, USL is the upper specification limit, and LSL is the lower specification limit.

The formula for k used here is given by Kane (1986). Note that k is sometimes computed without taking the absolute value of 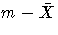$m - \bar{X}$ in the numerator. See Wadsworth et al. (1986).

If you do not specify the upper and lower limits in the SPEC statement or the SPEC= data set, then k is assigned a missing value.

Boyles' Index C_pm⁺

Boyles (1992) proposed the process capability index C_pm⁺ which is defined as

C_pm⁺ = (1/3) [ [( E_X<T [ (X-T)² ] )/( (T - LSL)² )] + [( E_X>T [ (X-T)² ] )/( (USL - T)² )] ] ^-1/2

He proposed this index as a modification of C_pm for use when 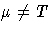$\mu \neq T$ .The quantities

$E_{X\lt T} [ (X-T)^2 ] = E [ (X-T)^2 | X \lt T ] Pr [ X \lt T ]$

and

$E_{X\gt T} [ (X-T)^2 ] = E [ (X-T)^2 | X \gt T ] Pr [ X \gt T ]$

are referred to as semivariances. Kotz and Johnson (1993) point out that if T = (LSL + USL ) / 2, then C_pm⁺ = C_pm.

Kotz and Johnson (1993) suggest that a natural estimator for C_pm⁺ is

$\hat{C}_{pm}^{+} = \frac{1}3 [ \frac{1}n \{ \frac{ \sum_{X_{i} \lt T} (X_{i... ...^2 } + \frac{ \sum_{X_{i} \gt T} (X_{i} - T)^2 }{ ({USL} - T)^2 } \}^{-1/2} ]$

Note that this index is not defined when either of the specification limits is equal to the target T. Refer to Section 3.5 of Kotz and Johnson (1993) for further details.

The Index C_jkp

Johnson et al. (1992) introduced a so-called "flexible" process capability index which takes into account possible differences in variability above and below the target T. They defined this index as

$C_{jkp} = \frac{1}{3 \sqrt{2}} \min ( \frac{{USL} - T}{ \sqrt{ E_{X\gt T}[(X-T)^2] } } , \frac{T - {LSL}}{ \sqrt{ E_{X\lt T}[(X-T)^2] } } )$

where d = ( USL - LSL ) / 2.

A natural estimator of this index is

$\hat{C}_{jkp} = \frac{1}{3 \sqrt{2}} \min ( \frac{ {USL} - T }{ \sqrt{ \sum... ...n } } , \frac{ T - {LSL} }{ \sqrt{ \sum_{X_{i} \lt T} (X_{i} - T)^2 / n } } )$

For further details, refer to Section 4.4 of Kotz and Johnson (1993).

The Indices C_pm(a)

The class of capability indices C_pm(a), indexed by the parameter a (a>0) allows flexibility in choosing between the relative importance of variability and deviation of the mean from the target value T.

The class defined as

$C_{pm}(a) = ( 1 - a \zeta^2 ) C_{p}$

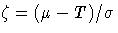where $\zeta = (\mu - T) / \sigma$ .The motivation for this definition is that if $|\zeta|$ is small, then

$C_{pm} \approx (1 - \frac{1}2 \zeta^2 ) C_p$

A natural estimator of C_pm(a) is

$\frac{d}{3s} \hat{C}_{pm}(a) = \{ 1 - a ( \frac{\bar{X}-T}s ) ^2 \}$

where d = ( USL - LSL ) / 2. You can specify the value of a with the CPMA= option in the PROC CAPABILITY statement. By default, a=0.5.

This index is not recommended for situation in which the target T is not equal to the midpoint of the specification limits.

For additional details, refer to Section 3.7 of Kotz and Johnson (1993).

The Index C_p(5.15)

Johnson et al. (1992) suggest the class of process capability indices defined as

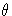$C_{p(\theta)} = \frac{{USL} - {LSL}}{\theta \sigma}$

where $\theta$ is chosen so that the proportion of conforming items is robust with respect to the shape of the process distribution. In particular, Kotz and Johnson (1993) recommend use of

$C_{p(5.15)} = \frac{{USL} - {LSL}}{5.15 \sigma}$

which is estimated as

$\hat{C}_{p(5.15)} = \frac{{USL} - {LSL}}{5.15 s}$

For details, refer to Section 4.3.2 of Kotz and Johnson (1993).

The Index C_pk(5.15)

Similarly, Kotz and Johnson (1993) recommend use of the robust capability index

$C_{pk(5.15)} = \frac{d - | \mu - ({USL} + {LSL}) / 2 | }{2.575 \sigma}$

where d = ( USL - LSL ) / 2. This index is estimated as

$\hat{C}_{pk(5.15)} = \frac{d - | \bar{X} - ({USL} + {LSL}) / 2 |}{2.575 s}$

For details, refer to Section 4.3.2 of Kotz and Johnson (1993).

The Index C_pmk

Pearn et al. (1992) proposed the index C_pmk

$C_{pmk} = \frac{({USL} - {LSL})/2 - |\mu - m |} {3 \sqrt{ \sigma^2 + (\mu - T)^2}}$

where m = ( LCL + UCL) / 2. A natural estimator for C_pmk is

$\hat{C}_{pmk} = \frac{({USL} - {LSL})/2 - |\bar{X} - m |} {3 \sqrt{(\frac{n-1}n)s^2 + (\bar{X} - T)^2}}$

where m = ( USL + LSL ) / 2.

For further details, refer to Section 3.6 of Kotz and Johnson (1993).

Wright's Index C_s

Wright (1995) defines the capability index

$C_s = \frac{ \min ( \rm{USL} - \mu, \mu - \rm{LSL} ) } { 3 \sqrt{ \sigma^2 + (\mu - T)^2 + \mu_3 / \sigma } }$

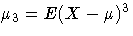where $\mu_3 = E(X - \mu)^3$ .

A natural estimator of C_s is

$\hat{C}_s = \frac{ ( \rm{USL} - \rm{LSL} ) / 2 - | \bar{X} - m | } { 3 \sqrt{ ( \frac{n-1}n ) s^2 + (\bar{X} - T)^2 + | c_4 s^2 b_3| } }$

where c₄ is an unbiasing constant for the sample standard deviation, and b₃ is a measure of skewness. Wright (1995) shows that C_s compares favorably with C_pmk even when skewness is not present, and he advocates the use of C_s for monitoring near-normal processes when loss of capability typically leads to asymmetry.

Chapter Contents
Previous
Next
Top