Chapter Contents
Previous
Next
|
Chapter Contents |
Previous |
Next |
| HISTOGRAM Statement |
The following sections provide information on the families of parametric distributions that you can fit with the HISTOGRAM statement. Properties of these distributions are discussed by Johnson et al. (1994, 1995).

whereNote: This notation is consistent with that of other distributions that you can fit with the HISTOGRAM statement. However, many texts, including Johnson et al. (1995), write the beta density function asand
lower threshold parameter (lower endpoint parameter)
scale parameter
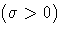
shape parameter
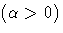
shape parameter
h = width of histogram interval

The two notations are related as follows:The range of the beta distribution is bounded below by a threshold parameter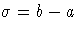
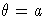
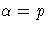
In addition, you can specify ![]() and
and ![]() with the ALPHA= and BETA= beta-options,
respectively. By default, the procedure calculates maximum
likelihood estimates for
with the ALPHA= and BETA= beta-options,
respectively. By default, the procedure calculates maximum
likelihood estimates for ![]() and
and ![]() . For example,
to fit a beta density curve to a set of data bounded below by
32 and above by 212 with maximum likelihood estimates
for
. For example,
to fit a beta density curve to a set of data bounded below by
32 and above by 212 with maximum likelihood estimates
for ![]() and
and ![]() , use the following statement:
, use the following statement:
histogram length / beta(theta=32 sigma=180);The beta distributions are also referred to as Pearson Type I or II distributions. These include the power-function distribution (
You can use the DATA step function BETAINV to compute beta quantiles and the DATA step function PROBBETA to compute beta probabilities.

whereThe threshold parameterthreshold parameter
scale parameter
h = width of histogram interval
The exponential distribution is a special case of
both the gamma distribution (with ![]() ) and
the Weibull distribution (with c=1). A related
distribution is the extreme value distribution.
If Y = exp(-X) has an exponential distribution, then
X has an extreme value distribution.
) and
the Weibull distribution (with c=1). A related
distribution is the extreme value distribution.
If Y = exp(-X) has an exponential distribution, then
X has an extreme value distribution.

whereThe threshold parameterthreshold parameter
scale parameter
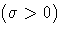
shape parameter
h = width of histogram interval

![p(x) = \{[2^{\frac{\nu}2-1}\Gamma(\frac{\nu}2)]
^{-1}x^{\nu-1} \exp(-\frac{x^2}2)
& {for x \gt 0} \ 0 & {for x \leq 0}
.](images/hsteq61.gif)
You can use the DATA step function GAMINV to compute gamma quantiles and the DATA step function PROBGAM to compute gamma probabilities.

whereThe SB distribution is bounded below by the parameterthreshold parameter
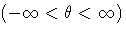
scale parameter
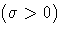
shape parameter

shape parameter
h = width of histogram interval
By default, the method of percentiles given by Slifker and Shapiro (1980) is used to estimate the parameters. This method is based on four data percentiles, denoted by x-3z, x-z, xz, and x3z, which correspond to the four equally spaced percentiles of a standard normal distribution, denoted by -3z, -z, z, and 3z, under the transformation

The following values are computed from the data percentiles:


If you specify FITMETHOD = MOMENTS (in parentheses after the SB option) the method of moments is used to estimate the parameters. If you specify FITMETHOD = MLE (in pareqntheses after the SB option) the method of maximum likelihood is used to estimate the parameters. Note that maximum likelihood estimates may not always exist. Refer to Bowman and Shenton (1983) for discussion of methods for fitting Johnson distributions.
![p(x) = \{ \frac{ \delta h x 100\%}{\sigma \sqrt{2\pi} }
\frac{ 1 }
{ \sqrt{ 1 ...
...}{\sigma} )
)^2
]
& {for x \gt \theta } \ 0 & {for x \leq \theta\space }
.](images/hsteq41.gif)
whereYou can specify the parameters with the THETA=, SIGMA=, DELTA=, and GAMMA= SU-options, which are enclosed in parentheses after the SU option. If you do not specify these parameters, they are estimated.location parameter
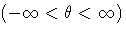
scale parameter
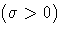
shape parameter

shape parameter
h = width of histogram interval
By default, the method of percentiles given by Slifker and Shapiro (1980) is used to estimate the parameters. This method is based on four data percentiles, denoted by x-3z, x-z, xz, and x3z, which correspond to the four equally spaced percentiles of a standard normal distribution, denoted by -3z, -z, z, and 3z, under the transformation

The following values are computed from the data percentiles:


If you specify FITMETHOD = MOMENTS (in parentheses after the SU option) the method of moments is used to estimate the parameters. If you specify FITMETHOD = MLE (in parentheses after the SU option) the method of maximum likelihood is used to estimate the parameters. Note that maximum likelihood estimates may not always exist. Refer to Bowman and Shenton (1983) for discussion of methods for fitting Johnson distributions.

wherethreshold parameter
scale parameter
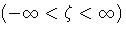
shape parameter
h = width of histogram interval
The threshold parameter ![]() must be less than the
minimum data value. You can specify
must be less than the
minimum data value. You can specify
![]() with the THRESHOLD= lognormal-option.
By default,
with the THRESHOLD= lognormal-option.
By default, ![]() .
If you specify THETA=EST, a maximum likelihood estimate
is computed for
.
If you specify THETA=EST, a maximum likelihood estimate
is computed for ![]() .You can specify
.You can specify ![]() and
and
![]() with the SCALE= and SHAPE=
lognormal-options, respectively. By default, the
procedure calculates maximum likelihood estimates for these
parameters.
with the SCALE= and SHAPE=
lognormal-options, respectively. By default, the
procedure calculates maximum likelihood estimates for these
parameters.
Note: The lognormal distribution is also referred to as the SL distribution in the Johnson system of distributions.
Note: This book uses ![]() to denote the shape
parameter of the lognormal distribution, whereas
to denote the shape
parameter of the lognormal distribution, whereas ![]() is used to denote the scale parameter of the beta,
exponential, gamma, normal, and Weibull distributions.
The use of
is used to denote the scale parameter of the beta,
exponential, gamma, normal, and Weibull distributions.
The use of ![]() to denote the lognormal shape parameter is
based on the fact that
to denote the lognormal shape parameter is
based on the fact that ![]() has a standard normal distribution if X is lognormally
distributed.
has a standard normal distribution if X is lognormally
distributed.

You can specify
wheremean
standard deviation
h = width of histogram interval
You can use the DATA step function PROBIT to compute normal quantiles and the DATA step function PROBNORM to compute probabilities.
Note: The normal distribution is also referred to as the SN distribution in the Johnson system of distributions.

wherethreshold parameter
scale parameter
c = shape parameter (c >0) h = width of histogram interval
The threshold parameter ![]() must be less than the minimum
data value. You can specify
must be less than the minimum
data value. You can specify
![]() with the THRESHOLD= Weibull-option.
By default,
with the THRESHOLD= Weibull-option.
By default, ![]() .
If you specify THETA=EST, a maximum likelihood estimate
is computed for
.
If you specify THETA=EST, a maximum likelihood estimate
is computed for ![]() .You can specify
.You can specify ![]() and c with the SCALE= and SHAPE= Weibull-options,
respectively. By default, the procedure calculates
maximum likelihood estimates for
and c with the SCALE= and SHAPE= Weibull-options,
respectively. By default, the procedure calculates
maximum likelihood estimates for ![]() and c.
and c.
The exponential distribution is a special case of the Weibull distribution where c=1.
|
Chapter Contents |
Previous |
Next |
Top |
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.