General Form of an Estimable Function

The Four Types of Estimable Functions

General Form of an Estimable Function

This section demonstrates a shorthand technique for displaying the generating set for any estimable L. Suppose

$X = [ 1 & 1 & 0 & 0 \ 1 & 1 & 0 & 0 \ 1 & 0 & 1 & 0 \ 1 & 0 & 1 & 0 \ 1 & 0 & 0 & 1 \ 1 & 0 & 0 & 1 ] { and } {\beta}= [ \mu \ A_1 \ A_2 \ A_3 ]$

X is a generating set for L, but so is the smaller set

${X^*} = [ 1 & 1 & 0 & 0 \ 1 & 0 & 1 & 0 \ 1 & 0 & 0 & 1 \ ]$

X^* is formed from X by deleting duplicate rows.

Since all estimable Ls must be linear functions of the rows of X^* for $L {\beta}$ to be estimable, an L for a single-degree-of-freedom estimate can be represented symbolically as

L1 ×(1 1 0 0) + L2 ×(1 0 1 0) + L3 ×(1 0 0 1)

L = (L1+L2+L3, L1, L2, L3)

For this example, $L {\beta}$ is estimable if and only if the first element of L is equal to the sum of the other elements of L or if

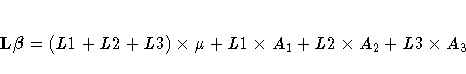
$L {\beta}= (L1+L2+L3) x \mu + L1 x A_1 + L2 x A_2 + L3 x A_3$

is estimable for any values of L1, L2, and L3.

If other generating sets for L are represented symbolically, the symbolic notation looks different. However, the inherent nature of the rules is the same. For example, if row operations are performed on X^* to produce an identity matrix in the first 3 ×3 submatrix of the resulting matrix

${X^{**}} = [ 1 & 0 & 0 & 1 \ 0 & 1 & 0 & -1 \ 0 & 0 & 1 & -1 ]$

then X^** is also a generating set for L. An estimable L generated from X^** can be represented symbolically as

L = (L1, L2, L3, L1-L2-L3)

Note that, again, the first element of L is equal to the sum of the other elements.

With the thousands of generating sets available, the question arises as to which one is the best to represent L symbolically. Clearly, a generating set containing a minimum of rows (of full row rank) and a maximum of zero elements is desirable. The generalized inverse of X'X computed by the GLM procedure has the property that (X'X)^-X'X usually contains numerous zeros. For this reason, PROC GLM uses the nonzero rows of (X'X)^-X'X to represent L symbolically.

If the generating set represented symbolically is of full row rank, the number of symbols (L1, L2, ... ) represents the maximum rank of any testable hypothesis (in other words, the maximum number of linearly independent rows for any L matrix that can be constructed). By letting each symbol in turn take on the value of 1 while the others are set to 0, the original generating set can be reconstructed.

Chapter Contents
Previous
Next
Top