Testing Linear Hypotheses

Introduction to Regression Procedures

Testing Linear Hypotheses

The general form of a linear hypothesis for the parameters is

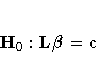
$H_0 : L {\beta}= c$

where L is q ×k, ${{\beta}}$ is k ×1, and c is q ×1. To test this hypothesis, the linear function is taken with respect to the parameter estimates:

Lb - c

This has variance

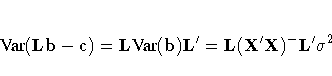
${Var} ({Lb} - c) = L {Var}(b) L^' = L(X^' X)^{-} L^' \sigma^2$

where b is the estimate of ${{\beta}}$ .

A quadratic form called the sum of squares due to the hypothesis is calculated:

SS(Lb - c) = (Lb - c)' (L(X' X)^- L')^-1 (Lb - c)

If you assume that this is testable, the SS can be used as a numerator of the F test:

F = [( SS(Lb - c) / q)/(s²)]

This is compared with an F distribution with q and dfe degrees of freedom, where dfe is the degrees of freedom for residual error.

Chapter Contents
Previous
Next
Top