Kernel Density Estimates

The KDE Procedure

Kernel Density Estimates

A weighted univariate kernel density estimate involves a variable X and a weight variable W. Let (X_i,W_i), i = 1,2, ... ,n denote a sample of X and W of size n. The weighted kernel density estimate of f(x), the density of X, is as follows:

$\hat{f}(x) = \frac{1}{\sum_{i=1}^n W_{i}} \sum_{i=1}^n W_{i} \varphi_{h}(x-X_{i})$

where h is the bandwidth and

$\varphi_{h}(x) = \frac{1}{\sqrt{2\pi}h} \exp ( -\frac{x^2}{2h^2} )$

is the standard normal density rescaled by the bandwidth. If

and $nharrow \infty$ , then the optimal bandwidth is

$h_{AMISE} = [ \frac{1}{2\sqrt{\pi} n \int(f'')^2} ]^{1/5}$

This optimal value is unknown, and so approximations methods are required. For a derivation and discussion of these results, refer to Silverman (1986, Chapter 3) and Jones, Marron, and Sheather (1996).

For the bivariate case, let X = (X,Y) be a bivariate random element taking values in $\Re^2$ with joint density function $f(x,y), (x,y) \in \Re^2$ , and let X_i = (X_i,Y_i), i = 1,2, ... , n be a sample of size n drawn from this distribution. The kernel density estimate of f(x,y) based on this sample is

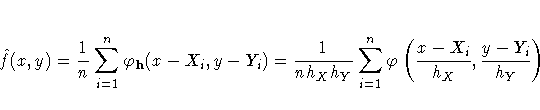
$\hat{f}(x,y) = \frac{1}n \sum_{i=1}^n \varphi_{h}(x-X_{i},y-Y_{i}) = \frac{1}{... ...}h_{Y}} \sum_{i=1}^n\varphi ( \frac{x-X_{i}}{h_{X}}, \frac{y-Y_{i}}{h_{Y}} )$

where $(x,y) \in \Re^2$ , h_X>0 and h_Y>0 are the bandwidths and $\varphi_{h}(x,y)$ is the rescaled normal density:

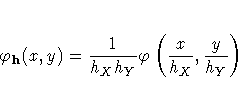
$\varphi_{h}(x,y) = \frac{1}{ h_{X}h_{Y}} \varphi ( \frac{x}{h_{X}}, \frac{y}{h_{Y}} )$

where $\varphi(x,y)$ is the standard normal density function:

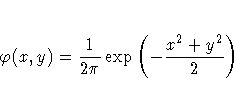
$\varphi(x,y) = \frac{1}{2\pi} \exp ( -\frac{x^2+y^2}2 )$

Under mild regularity assumptions about f(x,y), the mean integrated squared error of $\hat{f}(x,y)$ is

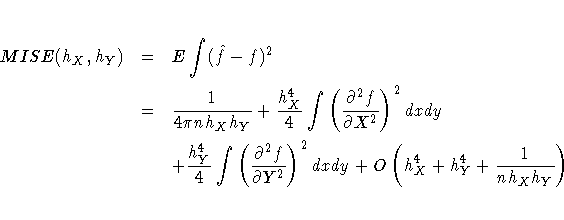
$MISE(h_{X},h_{Y}) & = & E\int(\hat{f}-f)^2 \ & = & \frac{1}{4\pi n h_{X} h_{Y}}+... ...ial^2f} {\partial Y^2})^2dxdy +O(h_{X}^4 + h_{Y}^4 + \frac{1}{ nh_{X}h_{Y}})$

as $h_{X} arrow 0$ , $h_{Y} arrow 0$ and $n h_{X} h_{Y} arrow \infty$ .

Now set

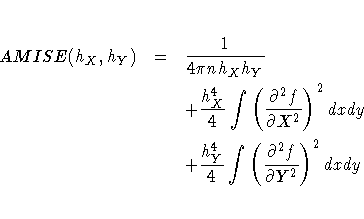
$AMISE(h_{X},h_{Y}) & = & \frac{1}{4\pi n h_{X} h_{Y}}\ & & +\frac{h_{X}^4}4\int(... ...2})^2dxdy \ & & +\frac{h_{Y}^4}4\int(\frac{\partial^2f} {\partial Y^2})^2dxdy$

which is the asymptotic mean integrated squared error. For fixed n, this has minimum at (h_{AMISE_X}, h_{AMISE_Y}) defined as

$h_{AMISE\_X} = [\frac{\int(\frac{\partial^2f} {\partial X^2})^2}{4n\pi}]^{1/6} ... ...tial^2f} {\partial X^2})^2}{\int(\frac{\partial^2f} {\partial Y^2})^2}]^{2/3}$

and

$h_{AMISE\_Y} = [\frac{\int(\frac{\partial^2f} {\partial Y^2})^2}{4n\pi}]^{1/6} ... ...tial^2f} {\partial Y^2})^2}{\int(\frac{\partial^2f} {\partial X^2})^2}]^{2/3}$

These are the optimal asymptotic bandwidths in the sense that they minimize MISE. However, as in the univariate case, these expressions contain the second derivatives of the unknown density f being estimated, and so approximations are required. Refer to Wand and Jones (1993) for further details.

Chapter Contents
Previous
Next
Top