Determining Observations for Likelihood Contributions

The LOGISTIC Procedure

Determining Observations for Likelihood Contributions

Suppose the response variable can take on the ordered values 1, ... , k, k+1 where k is an integer $\geq 1$ . If you use events/trials syntax, each observation is split into two observations. One has response value 1 with a frequency equal to the frequency of the original observation (which is 1 if the FREQ statement is not used) times the value of the events variable. The other observation has response value 2 and a frequency equal to the frequency of the original observation times the value of (trials - events). These two observations will have the same explanatory variable values and the same FREQ and WEIGHT values as the original observation.

For either single-trial or events/trials syntax, let j index all observations. In other words, for single-trial syntax, j indexes the actual observations. And, for events/trials syntax, j indexes the observations after splitting (as described previously). If your data set has 30 observations and you use single-trial syntax, j has values from 1 to 30; if you use events/trials syntax, j has values from 1 to 60.

The likelihood for the jth observation with ordered response value y_j and explanatory variables vector x_j is given by

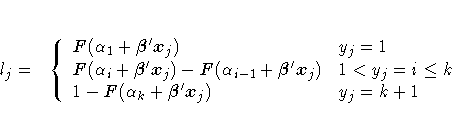
$l_j = & \{ F(\alpha_1+{\beta}'x_j) & y_j=1 \ F(\alpha_i+{\beta}'x_j)- F(\alpha_{i-1}+{\beta}'x_j) & 1\lt y_j=i\leq k \ 1-F(\alpha_k+{\beta}'x_j) & y_j=k+1 .$

where F(.) is the logistic, normal, or extreme-value distribution function, $\alpha_1, ... ,\alpha_{k}$ are intercept parameters, and ${\beta}$ is the slope parameter vector.

Chapter Contents
Previous
Next
Top