A classical problem of digital sequence design, first studied in the 1950s but still not well understood, is to determine those binary sequences whose non-trivial aperiodic autocorrelations are collectively small according to some suitable measure. The two principal such measures are the peak sidelobe level (PSL), which is the largest of their magnitudes, and the merit factor, which is based on their sum of squares. It has been known since 1968 that the PSL of almost all binary sequences of length n grows asymptotically no faster than order √(n log n). In 2007, Denis Dmitriev and I found numerical evidence that √(n log n) is the exact order of growth for almost all binary sequences; our experimental conclusion was proved by shortly afterwards by Alon, Litsyn and Shpunt, and the constant of proportionality was determined by Kai-Uwe Schmidt in 2014.

Is there a set of binary sequences whose PSL grows asymptotically more slowly than √(n log n)? The radar literature contains frequent assertions that the asymptotic PSL of m-sequences (also known as maximal length shift register sequences) grows no faster than order √n. In 2006, Kayo Yoshida and I carried out a historical and numerical investigation of this claim, concluding that it was not supported by theory or by data. In 2007, Denis Dmitriev and I discovered an algorithm that extends the range of exhaustive calculation for m-sequences, giving results up to sequence length 2²⁵–1. This provides the first numerical evidence that the PSL of almost all m-sequences actually grows exactly like order √n, and suggests that it will be advantageous to study the maximum PSL over all cyclic rotations of an m-sequence.

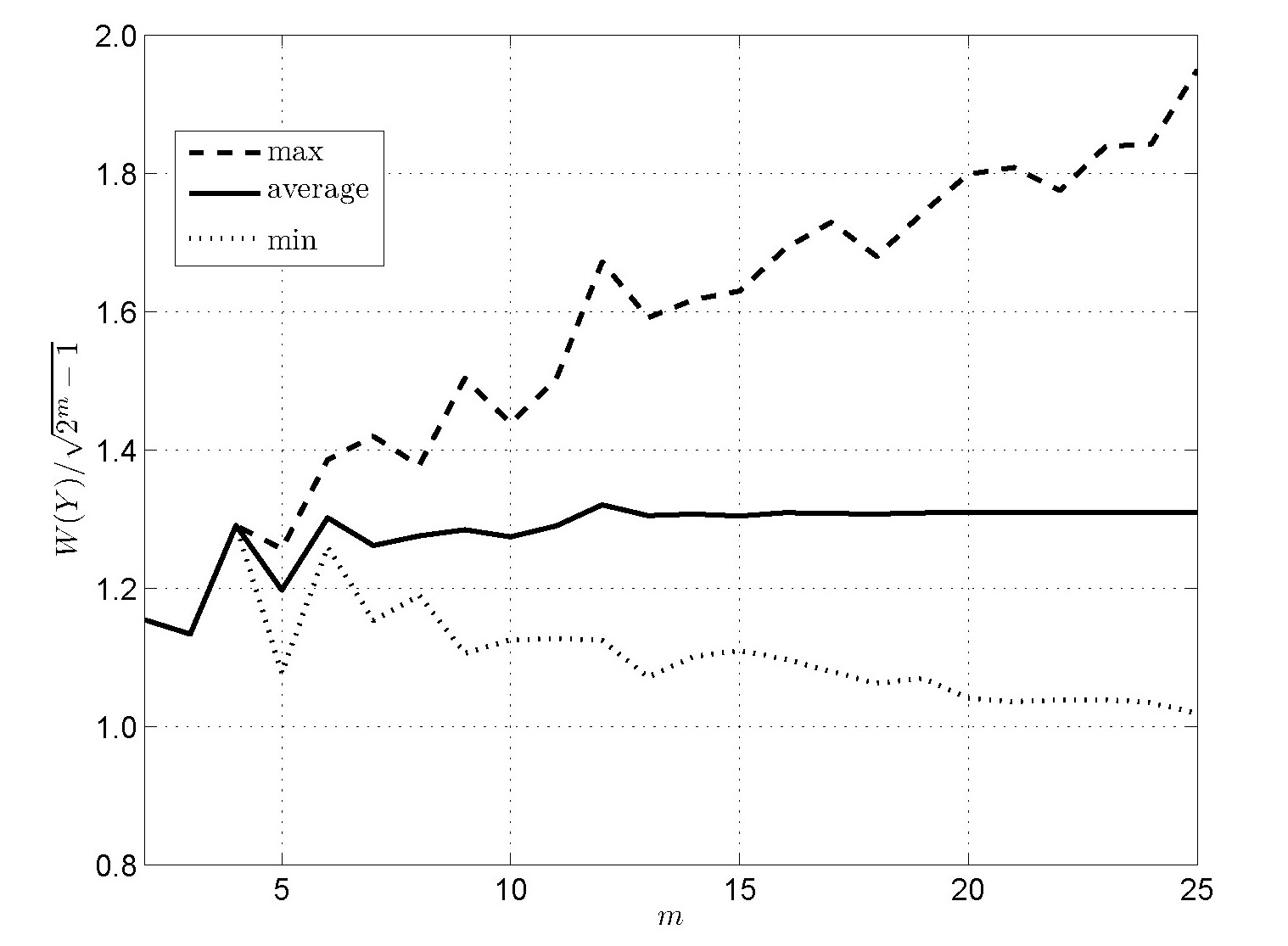
The growth, relative to √n, of the maximum PSL over all cyclic rotations of an m-sequence of length n.