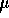 be the average weight of a month's production of coffee.
You are asked to choose between
be the average weight of a month's production of coffee.
You are asked to choose between 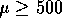 and
and 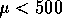 the
former being the manufacturer's claim. You have data
the
former being the manufacturer's claim. You have data  ,
a sample from this population and observe
,
a sample from this population and observe 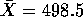 . The
manufacturer has also said
. The
manufacturer has also said 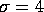 so we will use this in our test.
so we will use this in our test.
To assess the evidence against the manufacturers claim you make
that claim the null hypothesis: 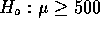 and
and 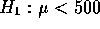 .
We use a z test (large sample size, known
.
We use a z test (large sample size, known 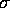 ) and get
) and get
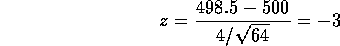
The alternative predicts large negative z so the P-value is the area under the normal curve to the left of -3 or about 0.0013. The conclusion is that this P-value is so small that the manufacturer's claim is not credible; the packages are underweight.
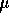 be the true concentration of cadmium in the lake.
You are being asked to choose between
be the true concentration of cadmium in the lake.
You are being asked to choose between 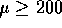 and
and  .
In this case you really ought to examine the data to see which, if either,
of these possibilities is ruled out. Thus you can either see right off that the
only possibility which might be ruled out is
.
In this case you really ought to examine the data to see which, if either,
of these possibilities is ruled out. Thus you can either see right off that the
only possibility which might be ruled out is  and make this
the null or you can do both tests. Either way the t-statistic (small
sample, hopefully normal population of concentration measurements) is
and make this
the null or you can do both tests. Either way the t-statistic (small
sample, hopefully normal population of concentration measurements) is
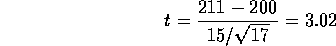
For  you get
you get 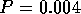 and for
and for 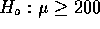 you get
you get  .
The first P-value means there is strong evidence against
.
The first P-value means there is strong evidence against  while the
second means there is little or no evidence against
while the
second means there is little or no evidence against 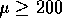 . The
clear real world conclusion is that the concentration of cadmium in the lake is
virtually certain to be over 200.
. The
clear real world conclusion is that the concentration of cadmium in the lake is
virtually certain to be over 200.
This conclusion summarizes the statistical calculations which rested on some assumptions. In practice there are serious potential problems which should be examined by the investigator (subject matter specialist not the statistician). Are the measurements unbiased? Are they independent or were they made in batches which would show more homogeneity within a batch than between? Are you really measuring the average concentration in the whole lake or only in a part of it?
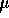 be the true average yield point of bars of the new
composition. We are told that we have a sample of size 25 from a normally
distributed population whose mean is
be the true average yield point of bars of the new
composition. We are told that we have a sample of size 25 from a normally
distributed population whose mean is  and whose SD is
and whose SD is 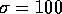 .
.
- The area to the left of 1.645 under a standard normal curve is
95% so a 90% confidence interval is given by the range
 or
or  .
.
- The multiplier changes from 1.645 to 1.75.
- You must solve the inequalities as follows
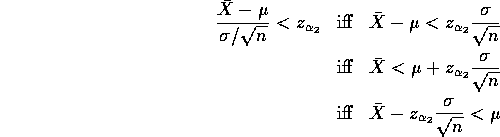
and similarly for the other inequality to get
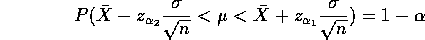
so that the two things on the outside are the interval.
- The lengths of the intervals are
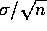 times
in one case
times
in one case 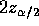 and in the other
and in the other  . For
. For 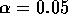 these lengths are
3.92 and 4.02 so that the usual interval is shorter. (It is
a theorem that using
these lengths are
3.92 and 4.02 so that the usual interval is shorter. (It is
a theorem that using 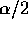 produces the shortest interval.)
produces the shortest interval.)
 and an approximate confidence interval
and an approximate confidence interval
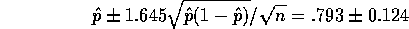
which is, as the text warns, quite wide. The sample size is not terribly large and you might worry about the normal approximation but for a rough idea the normal approximation is ok.
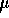 be the true average playing time of
this population of tapes (in practice --- what population of tapes?).
We have
be the true average playing time of
this population of tapes (in practice --- what population of tapes?).
We have  sampled from this population. We are given
sampled from this population. We are given
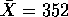 and s=8 and asked to use
and s=8 and asked to use 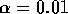 from which
the multiplier is
from which
the multiplier is  or so. The confidence interval
is then
or so. The confidence interval
is then 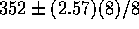 or
or  . This interval does
not contain 360 minutes so it is unlikely that
. This interval does
not contain 360 minutes so it is unlikely that 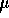 really is 360.
I think this data suggests strongly that the manufacturer is exaggerating.
This question would be answered by a hypothesis whose z statistic is
8 leading to a miniscule P-value. There is no doubt whatever that
really is 360.
I think this data suggests strongly that the manufacturer is exaggerating.
This question would be answered by a hypothesis whose z statistic is
8 leading to a miniscule P-value. There is no doubt whatever that
 is less than 6 hours.
is less than 6 hours.
- The null hypothesis of correct calibration is that
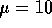 and the alternative is that it is not.
and the alternative is that it is not.
- The probability of recalibration is 1 minus the probability that the
sample average is between 9.8968 and 10.1032, that is,
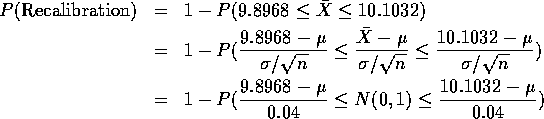
In this part you are told to take
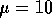 and get
and get
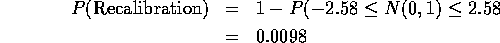
- Now you take
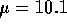 and get
and get
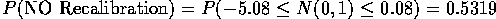
and then
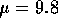 and get
and get 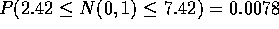 .
.
- You made this calculation in b above and got
 .
.
- Just by using n=10 in computing z. No change to c --
that's the point of computing z.
- This average can be computed by subtracting 10 and multiplying
by 1000 to get the numbers -19, 6, -143, 107, -112, -207, -272, 439,
214 and 190 whose sum is 203 so
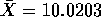 with n=10 so that
with n=10 so that
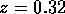 and the hypothesis is not rejected at the 1% level.
and the hypothesis is not rejected at the 1% level.
- Recalibrate if
 .
.