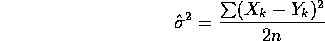STAT 330: 95-3

Assignment 4 Solutions

1. Chapter 6 Q 10:
   1. Recall the facts: 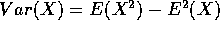, 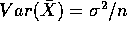and Then 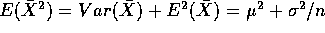which is more than so that is not an unbiased estimate of

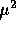
   2. On the other hand 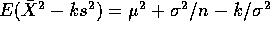which is 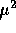if .

2. Chapter 6 Q 14:
   1. 525-202+1 = 324.

   2. This estimate will be right if we have seen the plane with the largest number and that with the smallest number. Otherwise our estimate is an underestimate. Thus the average value of our estimator (or its expected value) must be smaller than its largest possible value which is the true number of planes, that is, the parameter value. In other words this estimate (which happens to be the maximum likelihood estimate) is very biased.

3. Chapter 6 Q 16:
   1. so that this estimate is unbiased for any .

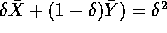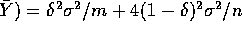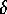   2. Var(Var(Var(. The derivative of this with respect to is 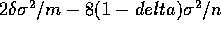which is 0 when 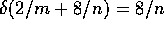or

      

   3. Chapter 6 Q 22: The first population moment, the mean, is

      

      This is equal to when or 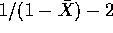. In this case 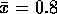and we get .

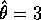   4. The likelih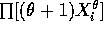ood is and the log likelihood is

      

      The derivative of this with respect to is 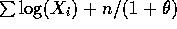which is 0 when 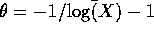which gives the estimate ?. (I haven't worked it out yet.)

4. Chapter 6 Q 32:
   1. The event 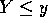is the same as the intersection of the events 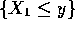, 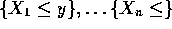. Since these events are independent we have, for ,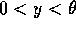

      

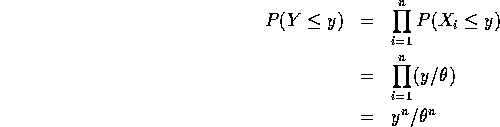
      The derivative of this with respect to y is the density of Y so the density is which is part a).

   2. We are asked to calculate the mean of Y which is

      

      which is not 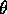. Thus Y is biased but 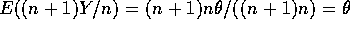so that is unbiased.

5. Chapter 6 Q 34:
   1. When the population distribution is normal we will see that 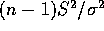has a chi-squared distribution with n-1 degrees of freedom, which is a Gamma distribution with shape and scale 2. This permits us to prove the hint since and 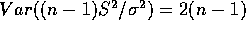. It follows that 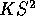has mean 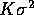, bias 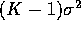and variance 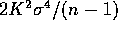. Thus the mean squared error of 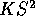is

      

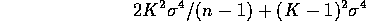
      which is a minimum when is minimized. Take the derivative with respect to K and set it equal to 0 to get 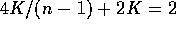whose solution is .

6. Chapter 6 Q 38:
   1. Here we have to multiply together the densitities of all the X's and all the Y's. If we take logarithms we get the following log likelihood:

      

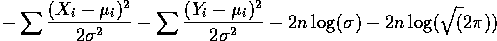
      The derivative with respect to 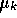is simply 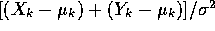which is 0 when 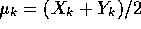. Put this in for each 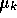and note that

      

      Now take the derivative with respect to 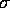to get

      

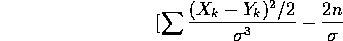
      which is 0 when

      

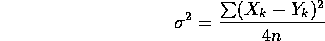
   2. The expected value of 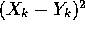is just 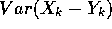because 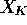and 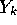have the same mean. But 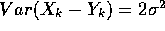so that the expected value of the mle is 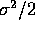. An unbiased estimate is obtained by multiplying by 2 to get

      

• About this document ...