- Chapter 11 Q4: I ran SAS and, after editing, I got the following
output:
General Linear Models Procedure
Dependent Variable: COVER
Sum of Mean
Source DF Squares Square F Value Pr > F
PAINT 3 296.25000000 98.75000000 10.97 0.0075
ROLLER 2 4.66666667 2.33333333 0.26 0.7798
Error 6 54.00000000 9.00000000
Corrected Total 11 354.91666667
R-Square C.V. Root MSE COVER Mean
0.847852 6.581353 3.0000000 45.583333
Tukey's Studentized Range (HSD) Test for variable: COVER
Alpha= 0.05 Confidence= 0.95 df= 6 MSE= 9
Critical Value of Studentized Range= 4.896
Minimum Significant Difference= 8.4794
Comparisons significant at the 0.05 level are indicated by '***'.
Simultaneous Simultaneous
Lower Difference Upper
PAINT Confidence Between Confidence
Comparison Limit Means Limit
1 - 2 -0.479 8.000 16.479
1 - 3 3.521 12.000 20.479 ***
1 - 4 3.854 12.333 20.813 ***
2 - 3 -4.479 4.000 12.479
2 - 4 -4.146 4.333 12.813
3 - 4 -8.146 0.333 8.813
I see a clear effect of paint brand but no visible effect of roller brand.
Brand 1 is better than 3 or 4 but not definitely better than 2. However,
even that difference is nearly significant.
- Chapter 11 Q 6: We find
 ,
,  and
and
 . The F statistic for the hypothesis of no difference
between assessors is
. The F statistic for the hypothesis of no difference
between assessors is  which is not significant at the
5% level (the
which is not significant at the
5% level (the 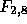 critical value is 4.46. The design is chosen to
make sure that variations between values for different assessors are not
due to house value differences. A design in which the different assessors
assessed different houses would be much less sensitive to small differences
between the assessors because the variation in value from house to house is
large compared to the likely size of the variation from assessor to
assessor. Note that the effect due to houses is large and statistically
significant but that no one would test this hypothesis since we all know
different houses have different values.
critical value is 4.46. The design is chosen to
make sure that variations between values for different assessors are not
due to house value differences. A design in which the different assessors
assessed different houses would be much less sensitive to small differences
between the assessors because the variation in value from house to house is
large compared to the likely size of the variation from assessor to
assessor. Note that the effect due to houses is large and statistically
significant but that no one would test this hypothesis since we all know
different houses have different values.
- Q 14:
Source SS df MS F P
A 30763 2 15381.5 3.79 0.037
B 34185.6 3 11728.5 2.81 0.061
A*B 43581.2 6 7263.5 1.79 0.144
Error 97436.8 24 4059.9
Total 205966.6 35
The interactions are not significant. The main effect of Factor A is marginally
significant while that of B is marginally not so. Generally it seems
likely that curing time has an effect on compressive strength and that
Factor B might do too. The Tukey intervals for  ,
,
 and
and  are all estimate pluss or
minus (2.92)(63.7)/
are all estimate pluss or
minus (2.92)(63.7)/ . (The number 63.7 is just
. (The number 63.7 is just  .)
NOTE: this is a typical exam type question.
.)
NOTE: this is a typical exam type question.
- Q16: I got the following from SAS. It shows no real evidence of
interactions (
 ) and significant main effects of both formula and
speed. It shows that the speed 70 gives a significantly lower yield than
either the lower or higher speed. To get estimates of the main effects you
need to average the columns and subtract the grand mean or average the top
9 numbers and bottom 9 numbers in the table and then subtract the grand
mean. I did not produce the probability plot though I think you know how to
do so with SAS.
) and significant main effects of both formula and
speed. It shows that the speed 70 gives a significantly lower yield than
either the lower or higher speed. To get estimates of the main effects you
need to average the columns and subtract the grand mean or average the top
9 numbers and bottom 9 numbers in the table and then subtract the grand
mean. I did not produce the probability plot though I think you know how to
do so with SAS.
General Linear Models Procedure
Dependent Variable: YIELD
Sum of Mean
Source DF Squares Square F Value Pr > F
FORMULA 1 2253.4422222 2253.4422222 376.27 0.0001
SPEED 2 230.8144444 115.4072222 19.27 0.0002
FORMULA*SPEED 2 18.5811111 9.2905556 1.55 0.2516
Error 12 71.8666667 5.9888889
Corrected Total 17 2574.7044444
R-Square C.V. Root MSE YIELD Mean
0.972087 1.391696 2.4472206 175.84444
Tukey's Studentized Range (HSD) Test for variable: YIELD
Alpha= 0.05 Confidence= 0.95 df= 12 MSE= 5.988889
Critical Value of Studentized Range= 3.773
Minimum Significant Difference= 3.7693
Comparisons significant at the 0.05 level are indicated by '***'.
Simultaneous Simultaneous
Lower Difference Upper
SPEED Confidence Between Confidence
Comparison Limit Means Limit
80 - 60 -2.719 1.050 4.819
80 - 70 4.297 8.067 11.836 ***
70 - 60 -10.786 -7.017 -3.247 ***
- Q48: I used proc glm with the statement model smooth = method
fabric to get the following output which shows a very clear effect of
drying method. There is no need to look at the effect of fabric; as a
blocking variable it would be surprising if it did not have an effect.
Tukey's procedure shows that drying methods are divided into two groups:
methods 1 and 3 giving significantly less smoothness than 2, 4 or 5.
Note that I have rearranged the SAS output to match the form in the text.
General Linear Models Procedure
Dependent Variable: SMOOTH
Sum of Mean
Source DF Squares Square F Value Pr > F
FABRIC 8 9.69600000 1.21200000 11.89 0.0001
METHOD 4 14.96222222 3.74055556 36.70 0.0001
Error 32 3.26177778 0.10193056
Corrected Total 44 27.92000000
R-Square C.V. Root MSE SMOOTH Mean
0.883174 12.94320 0.3192657 2.4666667
Tukey's Studentized Range (HSD) Test for variable: SMOOTH
Alpha= 0.05 df= 32 MSE= 0.101931
Critical Value of Studentized Range= 4.086
Minimum Significant Difference= 0.4349
Means with the same letter are not significantly different.
Tukey Grouping Mean N METHOD
A 3.3556 9 1
A
A 2.9556 9 3
B 2.0222 9 4
B
B 2.0111 9 5
B
B 1.9889 9 2
- Q 50: Most students will simply have done a two way anova on this
data set and found no significant effect of Sowing Rate. However, the very
high variability within plot 1 and low variability within plots 3 and 4
suggests that the assumption of constant
 is probably wrong. There
is a test, called Tukey's one degree of freedom test for non-additivity
which would have suggested a transformation is needed. I analyzed the
logarithms of the clover accumulations and concluded that there probably is
a difference. First the SAS code:
is probably wrong. There
is a test, called Tukey's one degree of freedom test for non-additivity
which would have suggested a transformation is needed. I analyzed the
logarithms of the clover accumulations and concluded that there probably is
a difference. First the SAS code:
options pagesize=60 linesize=80;
data Q50;
infile 'q50.dat';
input plot rate clover;
logcl=log(clover);
proc glm data=Q50;
class plot rate;
model logcl = plot rate;
means rate / tukey cldiff alpha=0.05;
run;
and some of the output:
General Linear Models Procedure
Dependent Variable: LOGCL
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 6 24.064 4.0107 19.91 0.0001
Error 9 1.813 0.2014
Corrected Total 15 25.877
Root MSE LOGCL Mean
0.4488151 6.1196277
Source DF Type I SS Mean Square F Value Pr > F
PLOT 3 16.740 5.58 27.70 0.0001
RATE 3 7.324 2.44 12.12 0.0016
Tukey's Studentized Range (HSD) Test for variable: LOGCL
Alpha= 0.05 Confidence= 0.95 df= 9 MSE= 0.201435
Critical Value of Studentized Range= 4.415
Minimum Significant Difference= 0.9907
Simultaneous Simultaneous
Lower Difference Upper
RATE Confidence Between Confidence
Comparison Limit Means Limit
13.5 - 10.2 -1.0257 -0.0350 0.9558
13.5 - 6.6 -0.3236 0.6671 1.6579
13.5 - 3.6 0.6426 1.6333 2.6241 ***
10.2 - 6.6 -0.2886 0.7021 1.6929
10.2 - 3.6 0.6776 1.6683 2.6590 ***
6.6 - 3.6 -0.0246 0.9662 1.9569
I have rearranged things. Note that the procedure analyzes means of
the logarithm not of the original variable. The conclusions are that
there is an effect to Sowing Rate and that the lowest level is definitely
worse than either of the two highest levels at producing clover.
To get the same analysis on the original scale you drop mention of logcl
and put clover in the model statement.
 ,
,  and
and
 . The F statistic for the hypothesis of no difference
between assessors is
. The F statistic for the hypothesis of no difference
between assessors is  which is not significant at the
5% level (the
which is not significant at the
5% level (the 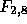 critical value is 4.46. The design is chosen to
make sure that variations between values for different assessors are not
due to house value differences. A design in which the different assessors
assessed different houses would be much less sensitive to small differences
between the assessors because the variation in value from house to house is
large compared to the likely size of the variation from assessor to
assessor. Note that the effect due to houses is large and statistically
significant but that no one would test this hypothesis since we all know
different houses have different values.
critical value is 4.46. The design is chosen to
make sure that variations between values for different assessors are not
due to house value differences. A design in which the different assessors
assessed different houses would be much less sensitive to small differences
between the assessors because the variation in value from house to house is
large compared to the likely size of the variation from assessor to
assessor. Note that the effect due to houses is large and statistically
significant but that no one would test this hypothesis since we all know
different houses have different values.
 ,
,
 and
and  are all estimate pluss or
minus (2.92)(63.7)/
are all estimate pluss or
minus (2.92)(63.7)/ . (The number 63.7 is just
. (The number 63.7 is just  .)
NOTE: this is a typical exam type question.
.)
NOTE: this is a typical exam type question.
 ) and significant main effects of both formula and
speed. It shows that the speed 70 gives a significantly lower yield than
either the lower or higher speed. To get estimates of the main effects you
need to average the columns and subtract the grand mean or average the top
9 numbers and bottom 9 numbers in the table and then subtract the grand
mean. I did not produce the probability plot though I think you know how to
do so with SAS.
) and significant main effects of both formula and
speed. It shows that the speed 70 gives a significantly lower yield than
either the lower or higher speed. To get estimates of the main effects you
need to average the columns and subtract the grand mean or average the top
9 numbers and bottom 9 numbers in the table and then subtract the grand
mean. I did not produce the probability plot though I think you know how to
do so with SAS.
 is probably wrong. There
is a test, called Tukey's one degree of freedom test for non-additivity
which would have suggested a transformation is needed. I analyzed the
logarithms of the clover accumulations and concluded that there probably is
a difference. First the SAS code:
is probably wrong. There
is a test, called Tukey's one degree of freedom test for non-additivity
which would have suggested a transformation is needed. I analyzed the
logarithms of the clover accumulations and concluded that there probably is
a difference. First the SAS code: