STAT 330 Lecture 12
Reading for Today's Lecture: 6.1, 6.2
Goals of Today's Lecture:
Today's notes
Data: 
(or more general is possible).
Model: A family 
of possible
densities for the data or a family 
of
possible cumulative distribution functions for the data.
Example:
Model: independent and each 
has density
where 
is a vector of two parameters.
(Other examples might be iid with density
for x>0 or iid Poisson 
or 
.)
Point estimate:
is a ``statistic'' (meaning function of the data) which is a guess for
.
Examples: 
, 
, 
, etc.
Principles of Estimation
The quality of 
is measured by averaging over all
possible data sets not just by looking at the actual data set you have.
The resulting measure of quality usually depends on the true value
of .
[Aside: I have just stated the frequentist philosophy; another, increasingly popular view, is that of the Bayesian statistician - see STAT 460.]
First idea: 
should be small. So some have
suggested averaging the quantity , that is
computing
Definition: is unbiased if 
for all , that is,
Examples:
A: . Then
B: 
.
Now use the following property of variance:
and rearrange it to get
.
We use this both for 
and for 
to get
and
Put these all together to get
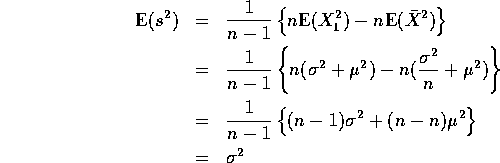
so that 
is an unbiased estimate of 
.
WARNING: 
because:
or
But 
so
and, taking square roots,
More examples: 
and 
are all unbiased estimates of the obvious parameters.
Criticism of unbiasedness:
Large negative errors can be balanced out by large positive errors.
Definition: The Mean Squared Error (abbreviated to MSE) of
is
There is a close relation between the MSE, the variance and the bias.
To show it use the temporary notation 
. Then
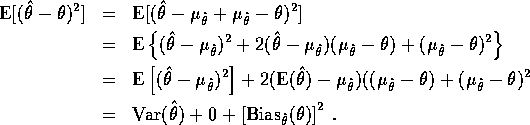
So: a good estimate has small bias and small variance. In practice there is a trade-off, to get one small you have to make the other big.
Finding (good) Point Estimates
Method of Moments
Basic strategy: set sample moments equal to population moments and solve for the parameters.
Definition: The 
sample moment (about the origin)
is
The population moment is
(Central moments are
and
