STAT 330 Lecture 23

Reading for Today's Lecture: 10.2, 10.3.

Goals of Today's Lecture:

• Derive Tukey's multiple comparison intervals for pairwise differences.
• Discuss interpretation of multiple comparison conclusions.

Today's notes

Confidence Intervals

One at a time confidence intervals for differences between group means, that is, for :

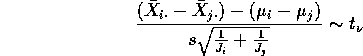
where is the degrees of freedom used in computing the MSE and

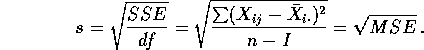
Problem: If, for example, I=4 then there are 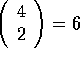pairs so there are 6 confidence intervals. If each interval has a 5% chance of missing its target then

and

For purposes of interpretation we often pick out the ``most interesting'' looking interval but we want

Tukey's Studentized Range Procedure

Suppose that are iid N(0,1) and where is independent of the Z's. Then we can choose constants so that

Tukey applied this to

in the case where and with

In this case we have that all r and t

with probability . But

but with the 2 sample pooled estimate of the standard deviation replaced by the root mean squared error, .

If we solve the inequality

we get a confidence interval for of the form

These are called simultaneous (for all r and t) confidence intervals because

Example: With I=4, J=6, n=24 the t type multiplier is so that the one at a time confidence intervals would be

while the Tukey intervals have (see page 711 and 712, Table A.8) and the intervals are

or

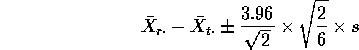
The Tukey multiplier of which is much wider than the one at a time confidence intervals. This extra width is required to control the overall error rate.

Unequal Sample Sizes

When the sample sizes are not all equal we make an approximation and replace by

and get intervals

The multiplier is larger than the usual for one at a time intervals.

Numerical Example: Coagulation Data

We have the 4 mean values 61, 66, 68 and 61 for diets A, B, C and D. The corresponding sample sizes are , and . We have , n=24, I=4, and . SO our 95% Tukey intervals are

Comparison Diff of Means

-5 4.28

-7 4.28

0 4.06

-2 3.82

5 3.58

7 3.58

Interpretation of Tukey Intervals

Typically we make a small dot plot of the means labelled by the group names and then underline those pairs of means where the difference is not significant, that is, where the Tukey interval includes 0. (The following example uses the numbers which will come out of an example in the next lecture.)

The conclusion is that is possible and is possible but that , , and .

Warning of potential problems

1: The following picture can arise:

A B C D

so that you know but think maybe and maybe .

2: It can also happen that when you do the F test of you reject but then when you look to see why you get the picture:

A B C D

Thus in this situation you are sure there are two different but not sure which two.