are independent random variables each having a
distribution. Let 
, 
,
, 
and 
.
Give the names for the distributions of each of 
, U, V, X and Y
and use tables to find 
, 
, 
,
, 
, 
.
for 
;
the new process is used to measure the concentrations for these samples.
It is thought likely that the concentrations measured by the new process,
which we denote 
, will be related to the true concentrations via
where the 
are independent, have mean 0 and all have the
same variance 
which is unknown.
- If this model is fitted by least squares, (that is by minimizing
) show that the least squares estimate of
is
- Show that the estimator in part (a) is unbiased.
- Compute (give a formula for) the standard error of
.
- The error sum of squares for this model is
which may be shown to have n-1 degrees of freedom.
If the 
are the numbers 1, 2, 3 and 4, 
and the
error sum of squares is 0.12 find a 95% confidence interval for 
and explain what further assumptions you must make to do so.
- Show that the estimator
is also unbiased.
- Compute (give a formula for) the standard error of
. Which
is bigger, the standard error of 
or that of 
?
- Show that the mle of
in this model is 
, the least
squares estimate, if the 
have normal distributions.
for
and 
. We generally fit a so-called additive model
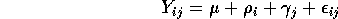
In the following questions consider the case I=2 and J=3.
- If we treat
, 
, 
, 
, 
and 
as the entries in the parameter vector 
what is the design matrix 
and what
is the rank of 
?
- What is the determinant of the matrix
? Is this matrix invertible? How many
solutions do the normal equations have?
- Usually we impose the restrictions
and 
.
Use these restrictions to eliminate 
and 
from the model equation
and, for the parameter vector 
find the design
matrix 
.
- An alternate set of restrictions is called corner point coding where we assume
. With this restriction and the parameter vector
what is the design matrix 
?
- Show that the three design matrices have the same column space by finding a matrix
A such that
and similarly for 
and 
and for 
and 
.
- Use the previous part to show that the vectors of fitted values
will be the
same for any solution of the normal equations for any of the three design matrices.