STAT 350

Assignment 2

1. In this problem you will prove that

   

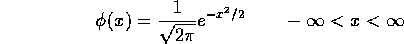
   is a density.

   1. Let 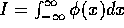. Show that

      

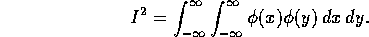
      HINT: What is 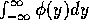in terms of I.

   2. Now if

      

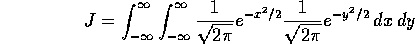
      do the double integral J in polar co-ordinates (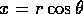, 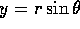) to show J=1.

   3. Deduce that 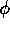is a density.

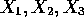2. Suppose are independent 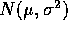random variables, so that 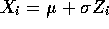with 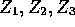independent standard normals.
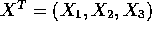   1. If and 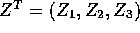express X in the form AZ+b for a suitable matrix A and vector b.
   2. Show that X is 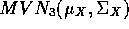and identify 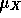and .
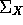   3. Let 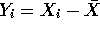for i=1,2,3 and 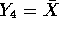. Show that 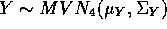and find 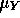and .

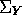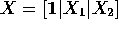3. Working with partitioned matrices. Suppose that the design matrix X is partitioned as where 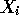has 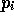columns.
   1. Write as a partitioned (3 rows, 3 columns) matrix.
   2. A matrix

      

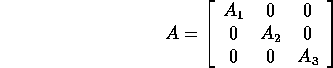
      is called block diagonal. Show that 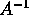exists if and only if each 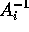exists and that then 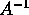is block diagonal.

   3. Suppose that for i=1,2 and 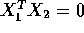. Show that is block diagonal and give a formula for .
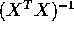   4. Suppose 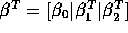is partitioned to conform with the partitioning of X (that is 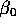is a scalar and 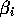is a column vector of length 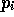for i=1,2. Let 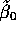be obtained by fitting

      

      by least square, 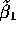be obtained by fitting

      

      and similarly for 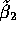. Let 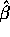be the usual least squares estimate for

      

      Show that .

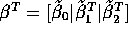   5. Let 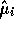be the vectors of fitted values corresponding to the estimates 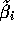for i=1,2,3. Show that for 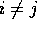we have .
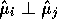   6. For the design matrix 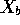of the first assignment identify 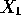and 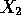and verify the orthogonality condition of this problem.
4. Page 321. Problem 7.33 parts a, b, e and f, 7.34 and 7.35 part a.

DUE: Monday, 27 January

• About this document ...