STAT 350: Lecture 24

Categorical covariates

• Data ; i labels level of covariate.
• Additive Model:

  

• Alternative form of same model:

  

• Possible linear restrictions on 's.

  

  or

  

Example

Consider a small version of the car mileage example on assignment 3. Imagine we have only the 5 data points below.

VEHICLE 1 VEHICLE 2

Mileage Emission Rate Mileage Emission Rate

0 50 0 40

1000 56 1100 49

2000 58

For the model equation

we have , . The are the 5 numbers 0, 1000, 2000, 0, 1100. For this parametrization the design matrix is

For the parametrization

the design matrix simply is that above with an extra column of 1's:

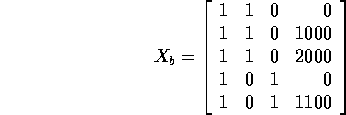
Since columns 2 and 3 add together to give the first column the matrix has rank 4 and is singular.

If we define the parameters , and then . As a result we can write the model equations as

and

and then the design matrix is

Alternatively corner point coding leads to the design matrix

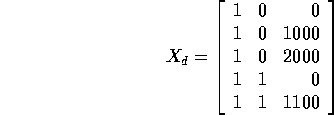
All these design matrixes have the same column spaces so they must lead to the same fitted values, same residuals and the same error sum of squares. The hypothesis of no "Vehicle" effect, that is, that the two cars have the same intercept is tested either by a t-test on the parameter which is the difference of intercepts or by an extra sum of squares F-test comparing with the restricted model in which just 1 straight line is fitted.

One important point is that in all the parametrizations the parameter "difference of intercepts" has the same estimate. This is true even for the matrix for which is singular.

Factors with more than two levels

Let us now examine what happens if we add two categorical variables, SCHOOL and REGION, to our model using sas.

SAS CODE

options pagesize=60 linesize=80;
data scenic;
 infile 'scenic.dat' firstobs=2;
 input Stay  Age Risk Culture Chest Beds School Region Census Nurses Facil;
 Nratio = Nurses / Census  ;
proc glm  data=scenic;
  class School Region;
  model Risk = Culture Stay Nurses Nratio School Region;
run ;
proc glm  data=scenic;
  class School Region;
  model Risk = Culture Stay Nurses School Region;
run ;
proc glm  data=scenic;
  class School Region;
  model Risk = Culture Stay Nurses Region;
run ;

EDITED OUTPUT

                           Class    Levels    Values
                           SCHOOL        2    1 2
                           REGION        4    1 2 3 4
Dependent Variable: RISK   
                        Sum of            Mean
Source     DF        Squares          Square   F Value     Pr > F
Model       8   110.94402256     13.86800282     15.95     0.0001
Error     104    90.43580045      0.86957500
Total     112   201.37982301
     R-Square      C.V.        Root MSE            RISK Mean
     0.550919   21.41305       0.9325101            4.3548673
Source     DF     Type I SS     Mean Square   F Value     Pr > F
CULTURE     1   62.96314170     62.96314170     72.41     0.0001
STAY        1   27.73884588     27.73884588     31.90     0.0001
NURSES      1    7.01369438      7.01369438      8.07     0.0054
NRATIO      1    5.97484076      5.97484076      6.87     0.0101
SCHOOL      1    1.24877748      1.24877748      1.44     0.2335
REGION      3    6.00472236      2.00157412      2.30     0.0815
Source     DF   Type III SS     Mean Square   F Value     Pr > F
CULTURE     1   27.43863928     27.43863928     31.55     0.0001
STAY        1   26.44898274     26.44898274     30.42     0.0001
NURSES      1    6.39021516      6.39021516      7.35     0.0079
NRATIO      1    1.74482880      1.74482880      2.01     0.1596
SCHOOL      1    2.21945688      2.21945688      2.55     0.1132
REGION      3    6.00472236      2.00157412      2.30     0.0815
________________________________________________________________
                     Sum of            Mean
Source     DF       Squares          Square   F Value     Pr > F
Model       7  109.19919376     15.59988482     17.77     0.0001
Error     105   92.18062925      0.87791075
Total     112  201.37982301
     R-Square      C.V.        Root MSE            RISK Mean
     0.542255   21.51544       0.9369689            4.3548673
Source     DF     Type I SS     Mean Square   F Value     Pr > F
CULTURE     1   62.96314170     62.96314170     71.72     0.0001
STAY        1   27.73884588     27.73884588     31.60     0.0001
NURSES      1    7.01369438      7.01369438      7.99     0.0056
SCHOOL      1    2.16544259      2.16544259      2.47     0.1193
REGION      3    9.31806922      3.10602307      3.54     0.0173
Source     DF   Type III SS     Mean Square   F Value     Pr > F
CULTURE     1   32.63679640     32.63679640     37.18     0.0001
STAY        1   24.70628794     24.70628794     28.14     0.0001
NURSES      1    8.99075614      8.99075614     10.24     0.0018
SCHOOL      1    3.19583271      3.19583271      3.64     0.0591
REGION      3    9.31806922      3.10602307      3.54     0.0173
________________________________________________________________
                     Sum of            Mean
Source     DF       Squares          Square   F Value     Pr > F
Model       6  106.00336105     17.66722684     19.64     0.0001
Error     106   95.37646196      0.89977794
Corrected Total     112     201.37982301
        R-Square    C.V.        Root MSE            RISK Mean
       .526385   21.78175       0.9485663            4.3548673
Source     DF     Type I SS     Mean Square   F Value     Pr > F
CULTURE     1   62.96314170     62.96314170     69.98     0.0001
STAY        1   27.73884588     27.73884588     30.83     0.0001
NURSES      1    7.01369438      7.01369438      7.79     0.0062
REGION      3    8.28767910      2.76255970      3.07     0.0310
Source     DF   Type III SS     Mean Square   F Value     Pr > F
CULTURE     1   30.50324858     30.50324858     33.90     0.0001
STAY        1   22.98974524     22.98974524     25.55     0.0001
NURSES      1    5.85040582      5.85040582      6.50     0.0122
REGION      3    8.28767910      2.76255970      3.07     0.0310

CONCLUSIONS

• Look at type III SS to see which effects can be deleted from full model. BUT, can only delete one at a time. Notice that NRATIO is least significant so drop it and refit.
• After refitting SCHOOL is not quite significant so delete and rerun. All remaining effects significant.
• Notice that F-test for REGION has 3 degrees of freedom. What is being tested is where these are 4 intercepts. Under the restricted model where this hypothesis is assumed there is 1 intercept compared to 4 intercepts in the full model. The difference of 3 is the degrees of freedom associated with the sum of squares for REGION.
• The TYPE III sums of squares are extra SS for comparing a model with all the effects in the model statement in proc glm to a model with one of those effects removed (but all the others still there).
• The TYPE I SS are also called sequential SS. They compare models which include all the factors down to a certain line in the table with the model including all the factors down to that line but not including the line. So, for example, the Type I SS for SCHOOL in the first model compares a model with CULTURE, STAY, NURSES and NRATIO to a model with all those variables plus SCHOOL. Neither model includes the line lower than SCHOOL in the table, that is, neither model includes REGION. All the TYPE I F-statistics use the ESS from the whole model fitted by GLM in the denominator (so the denominator estimate of in Type I SS test for Schools is the ESS from a model including REGION as well as all the other variables.