design matrix.
Let 
be the 
row of X (so that, 
is a column vector
or dimension p). Let 
be the design matrix with case i
deleted and 
the vector of n-1 responses with case i
deleted.
- Use partitioned matrices to show
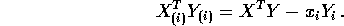
Write
and
Then
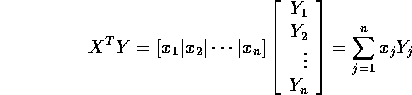
Since
and simply omit the ith rows we see
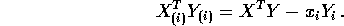
- Show
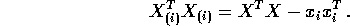
We have
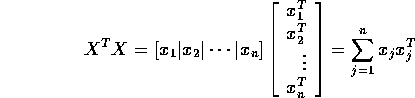
Again omitting the ith term we find
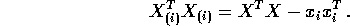
- Suppose B is an invertible symmetric
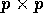matrix
and v is a column vector of dimension p. Show, by direct
multiplication, that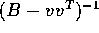 
is of the form
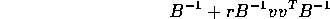
and give a formula for the scalar r.
Simply multiply
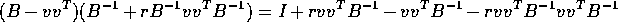
The trick most students missed is that in the last term the quantity
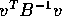is a scalar, that is, just a single number
(check that it is a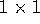 
matrix). It may help to give it a
name like s to see that the last term is
Thus
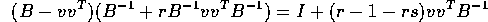
which is the identity matrix if
Solving gives
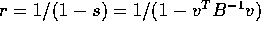. Many students
got a formula like
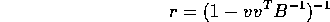
which is a
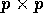matrix not a scalar. - Apply to previous part to show
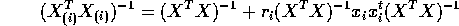
and give a formula for
in terms of the leverage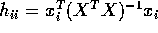 
.
Put
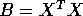and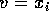 
. You get
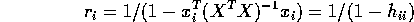
and
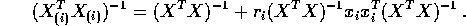
- Show
.
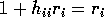We have
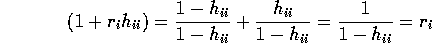
- Show that
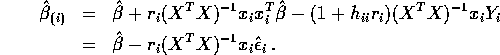
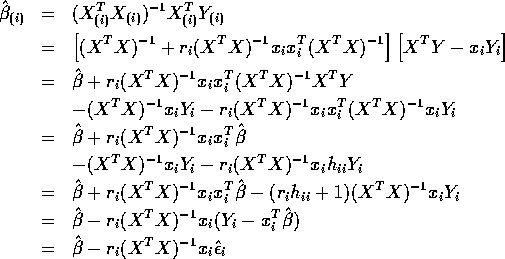
- Deduce that
.
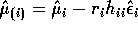Multiply
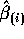by 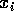to get
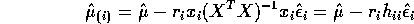
- Show that the 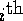PRESS residual
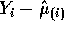is given by
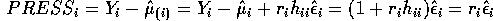
- Derive the formula for the
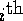externally studentized (case deleted) residual.
The variance of the PRESS residual is
.
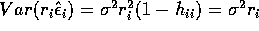The externally studentized residual is the PRESS residual divided
by an estimate of its standard error where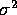 
is
estimated by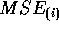 
. Thus the externally studentized residual
is
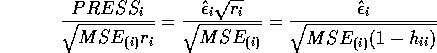
To get the simplest formula we must actually simplify
.
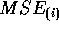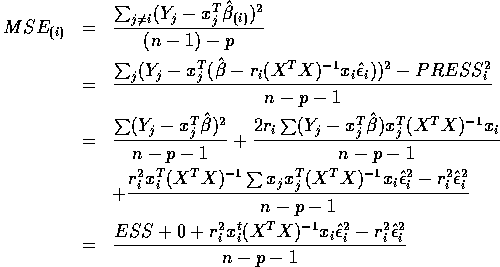
The middle term vanishes because
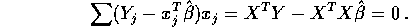
Use
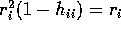to get
and then you can deduce the final formula given in class.
Here is code for all the methods and with all subsets done both
using 
and using adjusted 
.
data nit; infile 'nit.dat' ; input nitexc weight dryin wetin nitin ; proc reg data=nit; model nitexc = weight dryin wetin nitin /selection=FORWARD; run ; proc reg data=nit; model nitexc = weight dryin wetin nitin /selection=BACKWARD; run ; proc reg data=nit; model nitexc = weight dryin wetin nitin /selection=STEPWISE; run ; proc reg data=nit; model nitexc = weight dryin wetin nitin /selection=CP; run ; proc reg data=nit; model nitexc = weight dryin wetin nitin /selection=ADJRSQ; run ;
The conclusion of the
output
is that BACKWARD and STEPWISE settle
for the model containing only Nitrogen Intake as a predictor. The
forward selection method also includes Wet Intake because of the very high
level of 
(0.5) to enter. The all subsets method using
would settle on the model using only nitrogen intake but the adjusted
method also includes Wet Intake. However, overall there seems
little reason to include Wet Intake since it improves the fit very
little and is not very significant at all.
Here is code for the analysis of variance.
options pagesize=60 linesize=80; data electron; infile 'anova.dat' firstobs=2; input Time Sex Sequence Exper Replic; proc glm data=electron; class Sex Sequence Exper ; model time = Sex|Sequence|Exper ; means sex sequence exper sex*sequence*exper; estimate 'sexdif' sex 1 -1; estimate 'seq12dif' sequence 1 -1 0; estimate 'seq13dif' sequence 1 0 -1; estimate 'seq23dif' sequence 0 1 -1; estimate 'expdif' exper 1 -1; output out=anovres r=resid; proc rank data=anovres normal=blom out=ressc; var resid; ranks nscores; proc corr data=ressc; var resid nscores; run;COMMENTS
- You use the class statement to let SAS know that the factors are categorical.
- The model statement requests that all two way and the three way interaction terms be fitted.
- The means statement computes means and standard deviations for the groups defined by the levels of sex, of sequence, of exper and of all the 3 way combinations.
- The estimate statements compute the differences in means between the two sexes, between the 1st and second sequence, the first and third sequence and between the two levels of experience. This hinges on the use of a balanced design.
- The proc rank statements compute approximations to the expected values of normal order statistics needed for the correlation test in 23.12b.
- The correlation is actually computed by proc corr.
You can read the type III sums of squares table to do F tests without doing multiple runs because each effect has a sum of squares which is unaffected by the presence of the others. The conclusion is that the three way interaction is insignificant and all three two way interactions are insignificant. All three main effects are significant; none can be eliminated.
In the question on Bonferroni confidence intervals the 5 quantities to be estimated are each estimated by a difference of two averages so that the variance of the estimated difference is of the form
You work out standard t type confidence intervals by estimating
the means as usual (see the means statment) and replacing
by the MSE in the formula for the variance. The
Bonferroni method just replaces the of 0.01 by
for 5 confidence intervals. The t critical
value is 
. For the sex difference for instance the
average time for men is 1155.933 seconds while for women it is 966.1333.
The difference is 189.8 and this is computed by the means statement whose
output is
T for H0: Pr > |T| Std Error of Parameter Estimate Parameter=0 Estimate sexdif 189.800000 25.10 0.0001 7.56325180 seq12dif -57.250000 -6.18 0.0001 9.26305385 seq13dif 6.600000 0.71 0.4796 9.26305385 seq23dif 63.850000 6.89 0.0001 9.26305385 expdif 159.666667 21.11 0.0001 7.56325180
Notice the standard errors. The mean squared error in the model is 858.06. There
are 30 men and 30 women so the variance of the difference between men's average
and women's average is 858.06(1/30+1/30) = 57.204. The standard error of the estimate
of 
is then 
as in the
output. The desired confidence intervals are all and estimate from the column
labelled Estimate plus or minus 2.41 times a standard error from the last column.
The needed mean for 
is produced by means. The key point is that
the standard error to attach to the mean is 
which is based
on 48 degrees of freedom, not on 4.
For this question I used the SAS code
data knees; infile 'knees.dat' firstobs=2; input Days Fitness Patient Age ; proc glm data=knees; class Fitness ; model Days = Fitness|Age ; proc glm data=knees; class Fitness ; model Days = Fitness Age ; output out=anovres r=resid p=fitted; proc rank data=anovres normal=blom out=ressc; var resid; ranks nscores; proc corr data=ressc; var resid nscores; proc print data=ressc; var fitted fitness age resid nscores; run;getting the output ( complete output )
General Linear Models Procedure
Dependent Variable: DAYS
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 5 1082.0560870 216.4112174 655.36 0.0001
Error 18 5.9439130 0.3302174
Correctd Totl 23 1088.0000000
R-Square C.V. Root MSE DAYS Mean
0.994537 1.795767 0.5746454 32.000000
Source DF Type III SS Mean Square F Value Pr > F
FITNESS 2 5.44989183 2.72494592 8.25 0.0029
AGE 1 369.44147783 369.44147783 1118.78 0.0001
AGE*FITNESS 2 0.22183487 0.11091744 0.34 0.7191
General Linear Models Procedure
Dependent Variable: DAYS
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 1081.8342521 360.6114174 1169.72 0.0001
Error 20 6.1657479 0.3082874
Correctd Totl 23 1088.0000000
R-Square C.V. Root MSE DAYS Mean
0.994333 1.735114 0.5552363 32.000000
Source DF Type III SS Mean Square F Value Pr > F
FITNESS 2 246.08370505 123.04185252 399.11 0.0001
AGE 1 409.83425209 409.83425209 1329.39 0.0001
Correlation Analysis
Pearson Correlation Coefficients
RESID
NSCORES 0.99488
OBS FITTED FITNESS AGE RESID NSCORES
1 28.7930 1 18.3 0.20697 0.26136
2 42.4503 1 30.0 -0.45028 -0.87524
3 38.3648 1 26.5 -0.36478 -0.60318
4 40.2324 1 28.1 -0.23244 -0.48332
5 42.1001 1 29.7 0.89991 1.94690
6 39.8822 1 27.8 0.11775 0.05171
7 30.5440 1 19.8 -0.54396 -1.03865
8 41.6332 1 29.3 0.36682 0.73241
9 29.8639 2 20.8 0.13613 0.15568
10 34.9999 2 25.2 0.00007 -0.05171
11 39.6691 2 29.2 -0.66907 -1.23590
12 28.9300 2 20.0 -0.93004 -1.49843
13 30.6810 2 21.5 0.31903 0.60318
14 31.3813 2 22.1 -0.38134 -0.73241
15 28.5799 2 19.7 0.42015 0.87524
16 34.4163 2 24.7 0.58372 1.03865
17 29.1635 2 20.2 -0.16349 -0.26136
18 32.3152 2 22.9 0.68483 1.23590
19 25.2062 3 22.7 0.79380 1.49843
20 32.2099 3 28.7 -0.20991 -0.37006
21 20.7705 3 18.9 0.22949 0.37006
22 19.7199 3 18.0 0.28005 0.48332
23 24.0389 3 21.7 -1.03891 -1.94690
24 22.0545 3 20.0 -0.05452 -0.15568
For part a of 25.11 the residuals are printed out above. For part b the plots desired are:
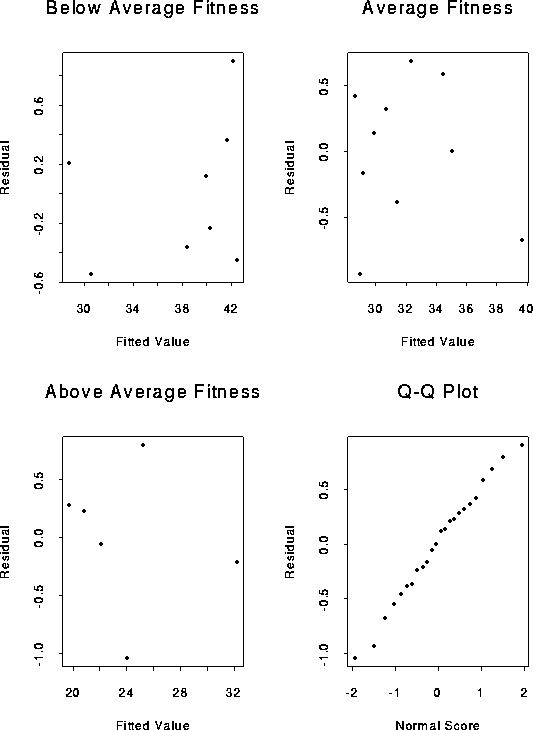
For part c, the generalized model is
and the null hypothesis is that all the 
are equal. This is tested by
comparing the two model statements
model days = fitness | age and model days = fitness age, doing an
extra sum of squares F test. The resulting F statistic is the
Type III sum of squares for fitness*age giving F=0.34 and P=0.7191.
The null hypothesis is accepted.
For 25.12 part c the F statistic is obtained from the Type III sum of squares for fitness for the model days = fitness age statement. This has F=399.11 and P=0.0001 There is clearly an effect of the variable Fitness.
The estimate statements permit us to compare the three levels of fitness. SAS prints out estimates of the differences in the intercepts. The relevant output is
T for H0: Pr > |T| Std Error of Parameter Estimate Parameter=0 Estimate High v Low Fitness -8.72289277 -26.20 0.0001 0.33296397 High v Med Fitness -6.87551411 -23.84 0.0001 0.28837673 Med v Low Fitness -1.84737866 -6.44 0.0001 0.28694289Notice that the fit group appears to recuperate about 9 days faster than the unfit group!