Postscript version of these notes

STAT 350: Lecture 7

Reading: 6.5, Chapter 15, Appendix A.

Selection of Model Order

An informal method of selecting p, the model order, is based on
$$\begin{align*}R^2 & = \mbox{squared multiple correlation} \\ & = \mbox{coeffici... ...le determination} \\ & = 1 - \frac{{\rm ESS}}{{\rm TSS(Adjusted)}} \end{align*}$$

Note: adding more terms always increases R².

Formal methods can be based on hypothesis tests. We can test $H_o:\beta_5 = 0$ and then, if we accept this test $H_o: \beta_4 = 0$ and then, if we accept that test $H_o: \beta_3=0$ and so on stopping when we first reject a hypothesis. This is ``backwards elimination''.

Justification: Unless $\beta_5=0$ there is no good reason to suppose that $\beta_4=0$ and so on.

Apparent conclusion in our example: p=5 is best; look at the P values in the SAS outputs.

Problems arising with that conclusion:

• p=5 gives lousy extrapolation

• there is no good physical meaning to a fifth degree polynomial model.

• there are too many parameters for n=10

• the correct relation is probably not best described by a polynomial. If, for instance, $\mu(t) = \alpha_0 e^{\alpha_1 t}$ then the best polynomial approximation might well have high degree.

Distribution Theory

Question: What is distribution theory?

Answer: How to compute the ``distribution'' of an estimator, test or other statistic, T:

• Find $P(T \le t)$, the Cumulative Distribution Function (CDF) of T.

• Find f_T(t) the density of T.

• Say something like ``T is N(12,25)'' or ``T is Binomial(100,0.75)'' or other named distribution. (Possible distributions include Normal, Binomial, t, Bernoulli, F, $\chi^2$, Gamma, Geometric, Negative Binomial, Poisson, Weibull, Logistic ...)

• Find ${\rm E}(T)$, ${\rm Var}(T)$ or other ``moments'' of T

In this course we

• do distribution theory when $\epsilon_i \sim N(0,\sigma^2)$

• discuss ``what if the errors, $\epsilon_i$ are not normal?''

The normal distribution

The standard normal density is

$$f(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2/2} \qquad -\infty < x < \infty$$

We say that $Z\sim N(0,1)$ if the density of Z is standard normal:

$$f_Z(t) = \frac{1}{\sqrt{2\pi}} e^{-t^2/2} \qquad -\infty < t < \infty$$

Reminder: if X has density f(x) then

$${\rm E}(g(X)) = \int_{-\infty}^\infty g(x)f(x) dx$$

So: $Z\sim N(0,1)$ implies

$${\rm E}(Z) = \int_{-\infty}^\infty \frac{z}{\sqrt{2\pi}} e^{-z^2/2} dz$$

but

$$\frac{d}{dz} e^{-z^2/2} = -ze^{-z^2/2}$$

so

$${\rm E}(Z) = \left. -\frac{1}{\sqrt{2\pi}} e^{-z^2/2}\right\vert _{-\infty}^\infty = 0$$

Next we compute the variance of Z remembering that ${\rm Var}(Z) = {\rm E}(Z^2) - ({\rm E}(Z))^2 = {\rm E}(Z^2)$:
$$\begin{align*}{\rm E}(Z^2) & = \int_{-\infty}^\infty \frac{z^2}{\sqrt{2\pi}} e^{-z^2/2} dz \\ & = \int u dv \end{align*}$$
where $u=-z/\sqrt{2\pi}$ and dv = -ze^-z2/2 dz. We do integration by parts and see that v=e^-z2/2 and $du=-dz/\sqrt{2\pi}$. This gives
$$\begin{align*}{\rm E}(Z^2) & =\int u dv \\ &= \left. uv\right\vert _{-\infty}^\... ...int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}} e^{-z^2/2} dz \\ & = 1 \end{align*}$$
because the integral of the normal density is 1. We have thus shown that

$${\rm Var}(Z) = 1$$

Definition: If $Z\sim N(0,1)$ then $X=\mu+\sigma Z\sim N(\mu,\sigma^2)$.

Note:

$$\begin{eqnarray*}{\rm E}(X) & = \mu+\sigma {\rm E}(Z) & = \mu \\ {\rm Var}(X) & = \sigma^2 {\rm Var}(Z) & = \sigma^2 \end{eqnarray*}$$

Definition: If $Z_1,\ldots,Z_n$ are independent N(0,1) then

$$Z = \left[ \begin{array}{c} Z_1 \\ \vdots \\ Z_n \end{array} \right] \sim MVN(0,I)$$

We say that the vector Z has a standard n-dimensional multivariate normal distribution.

We can define ${\rm E}(Z)$ and ${\rm Var}(Z)$ for vectors like Z as follows:

If X is a random vector of length n, say $X^T = \left[ X_1 \cdots X_n \right]$ then

$$\mu_X \equiv {\rm E}(X) = \left[ \begin{array}{c} {\rm E}(X_1) \\ \vdots \\ {\rm E}(X_n) \end{array} \right]$$

and ${\rm Var}(X)$ is an $n\times n$ matrix

$${\rm E}\left[ (X-\mu_X)(X-\mu_X)^T\right]$$

Note that the ijth entry of $(X-\mu_X)(X-\mu_X)^T$ is

$$(X_i - {\rm E}(X_i))(X_j-{\rm E}(X_j))$$

Definition:
$$\begin{align*}{\rm Cov}(X_i,X_j) & = {\rm E} \left[ (X_i - {\rm E}(X_i))(X_j-{\r... ...m E}(X_j)\right] \\ &= {\rm E}(X_i X_j) - {\rm E}(X_i){\rm E}(X_j) \end{align*}$$

Definition: If M is a matrix then ${\rm E}(M)$ is a matrix whose ijth entry is ${\rm E}(M_{ij})$.

So ${\rm Var}(X)$ has ijth entry ${\rm Cov}(X_i,X_j)$ and diagonal entries ${\rm Cov}(X_i,X_i) = {\rm Var}(X_i)$.

Extra integration examples

In class I started discussion of the Normal distribution. I computed the mean and variance of a standard normal and then of $N(\mu,\sigma^2)$. Here I will just show you a few more integrals:

The kth moment of a standard normal is

$$\int_{-\infty}^\infty t^k\phi(t)\,dt$$

We can do this integral by parts with u=-t^k-1 and $dv = -t\phi(t)\, dt$. This makes $v=\phi(t)$ and du = -(k-1)t^k-2dt so that by integration by parts

$$\begin{eqnarray*}\mu_k^\prime &=& uv\vert _{-\infty}^\infty +(k-1) \int_{-\infty}^\infty t^{k-2}\phi(t)\,dt \\ &=& \mu_{k-2}^\prime \end{eqnarray*}$$

Since $\mu_1^\prime=\mu=0$ and $\mu_2^\prime = 1$ we see that $\mu_k^\prime = 0$ if k is odd and $1\times 3\times\cdots \times (k-1)$ if k is even.

We can also compute the moment generating function of Z, that is,

$${\rm E}(e^{tZ}) = \int \frac{1}{\sqrt{2\pi}} \exp(tz-z^2/2)\, dz$$

by writing

$$tz-z^2/2 = -\frac{1}{2} (z-t)^2 +\frac{1}{2} t^2$$

and substituting u=z-t, du=dz in the integral to see that

$${\rm E}(e^{tZ}) = \int \frac{1}{\sqrt{2\pi}}\exp( -\frac{u^2}{2} +\frac{t^2}{2}) \, du = \exp(t^2/2) \, .$$

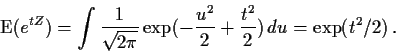
Now if $X\sim N(\mu,\sigma^2)$ then $Z=(X-\mu)/\sigma \sim N(0,1)$ so that the $k^{\rm th}$ central moment of X, namely $\mu_k = {\rm E}((X-\mu)^k)$ is 0 for odd k and $\sigma^k \times 1\times 3\times\cdots \times (k-1)$ for k even.

Similarly

$${\rm E}(e^{tX}) = e^{t\mu} {\rm E}(e^{\sigma t Z}) = \exp(t\mu+t^2\sigma^2/2) \, .$$

is the moment generating function of X.