Postscript version of these notes

STAT 350: Lecture 10

Reading: Chapter 6 sections 6, 7. See also chapter 17 section 3.

Example: Estimation of $\sigma$

Estimation of $\sigma^2$ is based on the error sum of squares defined by
$$\begin{align*}\mbox{ESS} & = \vert\vert\hat\epsilon\vert\vert^2 \\ & = \hat\eps... ...epsilon \\ & = \sum \hat\epsilon_i^2 \\ & = \epsilon^T M \epsilon \end{align*}$$
where
$$\begin{align*}M & = I-H \\ H & = X(X^TX)^{-1}X^T \end{align*}$$

We compute the mean of ESS as follows:
$$\begin{align*}{\rm E}[{\rm ESS}] & = {\rm E}(\epsilon^T M \epsilon) \\ & = {\rm... ...\sigma^2 I) \\ & = \sigma^2 {\rm trace}(M) \\ & = \sigma^2 ( n-p) \end{align*}$$

So:
$$\begin{align*}\hat\sigma^2 & = {\rm MSE} \qquad \mbox{(Mean Squared Error)} \\ & = \frac{{\rm ESS}}{n-p} \end{align*}$$
is an unbiased estimate of $\sigma^2$.

FACT: Every Sum of Squares we will see is of the form

$$Y^T QY = (X\beta+\epsilon)^T Q(X\beta+\epsilon)$$

for a suitable square, symmetric, matrix Q. The function

f(y) = y^tQy

is called a Quadratic Form.

FACT: Often we find

QX=0

so that

$$Y^T QY = \epsilon^T Q\epsilon$$

Example:
$$\begin{align*}MX &= (I - X (X^T X)^{-1}X^T) X \\ & = X - X (X^T X)^{-1}X^T X \\ & = X - X \\ & = 0 \end{align*}$$
So we find
$$\begin{align*}{\rm ESS} & = Y^T M Y \\ & = \epsilon^T M \epsilon \\ & = Y^T Y ... ... \\ & = {\rm TSS (unadjusted)} - { \rm Regression SS (unadjusted)} \end{align*}$$

Messages to take away from this example:

• The matrix algebra permits easy calculation of the expected value of a sum of squares.

• Sums of squares are often quadratic forms in the vector $\epsilon$ of errors.

We will follow up these points later. Now we turn to the third application of matrix algebra mentioned in lecture 9.

Inference for linear combinations of entries in $\beta$

Examples of linear combinations:

• Confidence intervals and tests for $\mu_x$, the mean of Ycorresponding to a particular value x of the covariate. (An example arises in extrapolation of our polynomial fit to times after the end of the data.)
  
  $$\hat\mu_x = x_1 \hat\beta_1 + \cdots + x_p \hat\beta_p = x^t \hat\beta$$
  
  

• Confidence intervals and tests for $\beta_k = [0,\ldots,0,1,0,\ldots, 0] \beta$ where the 1 is in position k.

Basic Ingredients:

1.

${\rm E} (x^t \hat\beta) = x^T \beta = \mu_x$.

2.

${\rm Var}(x^t \hat\beta) = x^T {\rm Var}(\hat\beta) x = \sigma^2 x^T (X^TX)^{-1} x$

3.

$\hat\sigma^2 = {\rm ESS}/(n-p)$ is consistent (that is, converges to $\sigma^2$ as $n\to \infty$).

4.

If $\epsilon_i\sim N(0,\sigma^2)$ or n is large then

$$\hat\beta \sim MVN(\beta,\sigma^2 (X^TX)^{-1})$$

5.

If as in 4 then

$$\hat\mu_x \sim MVN( \mu_x, \sigma^2 x^T (X^TX)^{-1} x)$$

6.

If $\epsilon_i\sim N(0,\sigma^2)$ then ${\rm ESS}/\sigma^2 \sim \chi^2_{n-p}$

7.

If $\epsilon_i\sim N(0,\sigma^2)$ then $\hat\beta$ is independent of ESS.

8.

If $\epsilon_i\sim N(0,\sigma^2)$ then

$$\frac{\hat\mu_x - \mu_x}{\hat\sigma\sqrt{x^T (X^TX)^{-1} x }} \sim t_{n-p}$$

9.

A confidence interval for $x^T \beta$ is

$$x^t \hat\beta \pm t_{\alpha/2,n-p} \sqrt{\frac{{\rm ESS}}{n-p}} \sqrt{x^T (X^TX)^{-1} x }$$

10.

The confidence interval in 9 is justified either by

• Normal errors OR

• large n

We have done the mathematics for 1, 2 ,4, 5 above. Fact number 8 is just the definition of the Student t distribution together with facts 5, 6 and 7. Fact number 9 is just the usual deduction of a confidence from the distribution of a pivot as in 8. I will wave my hands at the mathematics of 6 and 7 later in the course.

Example: Confidence intervals for $\mu_x$

Refer to the polynomial regression example (data on insurance costs). Suppose we are going to use a polynomial model of degree p and try to predict the costs for the first quarter of 1982, that is, for t=1982.25. Our model has

$$\mu_t = \beta_0 + (\beta_1 (t-1975.5) + \beta_2 (t-1975.5)^2 + \cdots$$

To make a prediction for t=1982.25 we estimate the $\beta$s and plug in 1982.25 for t giving the prediction
$$\begin{align*}\hat\mu_{1982.25} & = \hat\beta_0 + \hat\beta_1(1982.25-1975.5) + ... ...n{array}{c} \hat\beta_0 \\ \vdots \\ \hat\beta_p\end{array} \right] \end{align*}$$

Our confidence interval for the expected cost for 1982.25 is

$$\hat\mu_{1982.25} \pm t_{0.025,10-p-1} \underbrace{\sqrt{\rm MSE} \sqrt{x^T (X^TX)^{-1} x}}_{ \hat\sigma_{\hat\mu_{1982.25}}}$$

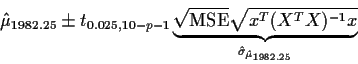
Here is a table of the computed confidence intervals:

Degree p	$\hat\mu$	t	$\hat\sigma_{\hat\mu}$	$\pm$
1	113.98	2.306	7.04	16.24
2	142.04	2.365	12.06	28.53
3	204.74	2.447	9.45	23.12
4	204.50	2.571	25.24	64.88
5	70.26	2.776	16.22	16.22

Notice that the forecasts for different polynomials are very diffferent and not within several standard errors of each other.

Problem: Let $\mu_x^*$ be the true mean of Y_x. Our MODEL says that $\mu_x^* = \mu_x = x^T\beta$ but most or all of these polynomials are WRONG.

You can see the principal by deleting the observation for 1980, then fitting the different polynomials, and predicting the 1980 value:

Degree	Estimate	SE
p	for 1980	of estimate
1	91.50	4.26
2	98.22	7.34
3	121.39	4.74
4	132.40	6.73
5	110.40	4.59

The true value of Y for 1980 is actually $115.19 so most of the forecasts would have been dreadful.

Predicting Y not $\mu$

The calculations given above provide confidence intervals for the expected value of Y for 1982.25. In fact each Y differs from its expected value by a random $\epsilon$. Thus the figure of $115.19 is not realy $\mu_{1980}$ bu Y₁₉₈₀.

To predict an observation, however, we guess $Y=\mu+\epsilon$ by guessing $\mu$ and adding a guess for $\epsilon$. Since $\epsilon$ is a mean 0 random variable, independent of all the other random variables used to predict $\mu$ we simply guess $\epsilon$ is 0 and use $\hat{Y} = \hat\mu$. But then

$$Y- \hat{Y} = Y - \hat\mu = (Y - \mu) + (\mu-\hat\mu) = \epsilon + (\mu-\hat\mu)$$

so that the error in predicting Y is the sum of two independent bits. We can compute the variance of this error:
$$\begin{align*}{\rm Var}(Y - \hat\mu) & = {\rm Var}(Y -\mu+(\mu-\hat\mu)) \\ & =... ...ar}(Y) + {\rm Var}(\hat\mu) \\ & = \sigma^2 ( 1+ x^T(X^TX)^{-1} x) \end{align*}$$

We call the square root of this quantity the root mean square , or RMS, Prediction Error and estimate this RMS prediciton error using

$$\hat\sigma\sqrt{1+ x^T(X^TX)^{-1} x}$$

For 1980 we get the following results:

Degree	$\hat\sigma_{\hat\mu}$	RMS Pred Err
1	42.6	7.25
3	4.74	5.22
5	4.59	4.63

The general formula for a level $1-\alpha$ prediction interval for Y_x is

$$x^T\hat\beta \pm t_{\alpha/2,n-p} \sqrt{{\rm MSE}} \sqrt{1+x^T(X^TX)^{-1} x}$$

Note that p is the number of columns of X in this general formula. For a degree k polynomial this p would be k+1.

Further discussion and SAS code

I fit polynomials of degree 1 through 5. Each model gives a vector of fitted parameters $\hat\beta$ and to predict the mean value of Y at time t we use $\hat\beta_0 + \hat\beta_1 t +\cdots + \hat\beta_p t^p$ when the fitted polynomial has degree p. The SAS code below computes both this fitted value and standard errors for each of the 5 models. Notice how I run proc glm 5 times to get the 5 different values.

data insure;
  infile 'insure.dat' firstobs=2;
  input year cost;
  code = year - 1975.5 ;
proc glm  data=insure;
   model cost = code ;
   estimate 'fit1982.25' intercept 1 code  6.75  / E;
run ;
proc glm  data=insure;
   model cost = code code*code;
   estimate 'fit1982.25' intercept 1 code  6.75 code*code 45.5625 / E;
run ;
proc glm  data=insure;
   model cost = code code*code code*code*code;
   estimate 'fit1982.25' intercept 1 code  6.75 code*code 
            45.5625 code*code*code 307.5469/ E;
run ;
proc glm  data=insure;
   model cost = code code*code code*code*code code*code*code*code;
   estimate 'fit1982.25' intercept 1 code  6.75 code*code 
            45.5625 code*code*code 307.5469 code*code*code*code  
            2075.9414 / E;
run ;
proc glm  data=insure;
   model cost = code code*code code*code*code code*code*code*code 
                code*code*code*code*code;
   estimate 'fit1982.25' intercept 1 code  6.75 code*code 
            45.5625 code*code*code 307.5469 code*code*code*code  
            2075.9414 code*code*code*code*code 14012.6045/ E;
run ;

The line estimate ... is probably unfamiliar to you. You have to give the values of each column of the design matrix at the place where you want to estimate $\mu_x$. Notice that I had to work out each power of 6.75 by hand. The / E piece causes SAS to print out the coefficients which are on the estimate line.

Now have a look at the edited output. I show here only the 5th degree polynomial results.

                        General Linear Models Procedure
Coefficients for estimate fit1982.25
INTERCEPT                                         1
CODE                                           6.75
CODE*CODE                                   45.5625
CODE*CODE*CODE                             307.5469
CODE*CODE*CODE*CODE                       2075.9414
COD*COD*COD*COD*CODE                     14012.6045

Dependent Variable: COST
                                     Sum of            Mean
Source              DF          Squares          Square   F Value     Pr > F

Model                5     3935.2507732     787.0501546   2147.50     0.0001
Error                4        1.4659868       0.3664967
Corrected Total      9     3936.7167600

              R-Square             C.V.        Root MSE            COST Mean
              0.999628         0.851438       0.6053897            71.102000

Source              DF        Type I SS     Mean Square   F Value     Pr > F
CODE                 1     3328.3209709    3328.3209709   9081.45     0.0001
CODE*CODE            1      298.6522917     298.6522917    814.88     0.0001
CODE*CODE*CODE       1      278.9323940     278.9323940    761.08     0.0001
CODE*CODE*CODE*CODE  1        0.0006756       0.0006756      0.00     0.9678
COD*COD*COD*COD*CODE 1       29.3444412      29.3444412     80.07     0.0009

Source              DF      Type III SS     Mean Square   F Value     Pr > F
CODE                 1       0.88117350      0.88117350      2.40     0.1959
CODE*CODE            1      20.86853994     20.86853994     56.94     0.0017
CODE*CODE*CODE       1      72.35876312     72.35876312    197.43     0.0001
CODE*CODE*CODE*CODE  1       0.00067556      0.00067556      0.00     0.9678
COD*COD*COD*COD*CODE 1      29.34444115     29.34444115     80.07     0.0009

                                    T for H0:    Pr > |T|   Std Error of
Parameter              Estimate    Parameter=0                Estimate
fit1982.25           70.2630583           4.33     0.0123     16.2154539

                                     T for H0:    Pr > |T|   Std Error of
Parameter               Estimate    Parameter=0                Estimate

INTERCEPT            64.88753906         176.14     0.0001     0.36839358
CODE                 -0.50238411          -1.55     0.1959     0.32399642
CODE*CODE             0.75623470           7.55     0.0017     0.10021797
CODE*CODE*CODE        0.80157430          14.05     0.0001     0.05704706
CODE*CODE*CODE*CODE  -0.00020251          -0.04     0.9678     0.00471673
COD*COD*COD*COD*CODE -0.01939615          -8.95     0.0009     0.00216764

While we have this output notice the value of R² which is quite close to 1 and the t-tests of hypotheses that various parameters are 0.

Here is a table of the results of all the forecasts with associated standard errors:

Degree	Estimate	SE
1	113.98	7.04
2	142.04	12.06
3	204.74	9.45
4	204.50	25.24
5	70.26	16.22

Notice that the standard errors are so small that there is no way that the forecasts from various different degree fits can be reconciled. The problem is that it is very likely that a crucial assumption is not right for this problem, namely, the assumption that the mean of Y is exactly a polynomial of degree 5 (or 3 or whatever). Notice also that adding a term to the model without improving the fit, as in going from degree 3 to degree 4, increases the SE of the prediction greatly.

One final point. The calculations give a confidence interval for $\mu_x$ based on the distribution of $\hat\mu_x-\mu_x$. For the insurance the quantity of interest is $Y_x-\hat\mu_x$. In this formula, Y_x is a future value associated with the covariate value x. The prediction can be split up, if the model is correct, as

$$Y_x-\hat\mu_x = (Y_x-\mu_x) +(\mu_x-\hat\mu_x)$$

which is a sum of two independent random variables. The first $Y_x-\mu_x$ has variance $\sigma^2$ while the second has variance $\sigma^2 x^t(X^TX)^{-1}x$. An estimate of the square root of the second quantity was printed out by SAS. The Mean Squared Error is an estimate of the first. The estimated standard deviation of $Y_x-\hat\mu_x$ is the square root of the sum of the squares of these two quantities which comes, for the 5th degree polynomial to $\sqrt{ 0.366 + (16.22)^2}$ which is only slightly larger, $16.23. Notice that this accuracy is spurious; the major source of error is in the model for the mean of Y which is surely not a 5th degree polynomial.

You can see the principal by deleting the observation for 1980 and then fitting the different polynomials:

Degree	Estimate	SE of $\hat\mu$	Prediction SE
1	91.50	4.26	7.25
2	98.22	7.34	9.34
3	121.39	4.74	5.22
4	132.40	6.73	6.95
5	110.40	4.59	4.63

The true value is actually $115.19 so most of the forecasts would have been dreadful.