Postscript version of this file

STAT 450 Lecture 15

Reading for Today's Lecture:

Goals of Today's Lecture:

• Introduce basic goals of statistical inference.

• Define likelihood, log-likelihood, score functions.

• Introduce maximum likelihood estimation.

Today's notes

Statistical Inference

Definition: A model is a family $\{ P_\theta; \theta \in \Theta\}$ of possible distributions for some random variable X. (Our data set is X, so X will generally be a big vector or matrix or even more complicated object.)

We will assume throughout this course that the true distribution P of Xis in fact some $P_{\theta_0}$ for some $\theta_0 \in \Theta$. We call $\theta_0$ the true value of the parameter. Notice that this assumption will be wrong; we hope it is not wrong in an important way. If we are very worried that it is wrong we enlarge our model putting in more distributions and making $\Theta$ bigger.

Our goal is to observe the value of X and then guess $\theta_0$ or some property of $\theta_0$. We will consider the following classic mathematical versions of this:

1.

Point estimation: we must compute an estimate $\hat\theta = \hat\theta(X)$ which lies in $\Theta$ (or something close to $\Theta$).

2.

Point estimation of a function of $\theta$: we must compute an estimate $\hat\phi = \hat\phi(X)$ of $\phi=g(\theta)$.

3.

Interval (or set) estimation. We must compute a set C=C(X) in $\Theta$ which we think will contain $\theta_0$.

4.

Hypothesis testing: We must decide whether or not $\theta_0\in\Theta_0$ where $\Theta_0 \subset \Theta$.

5.

Prediction: we must guess the value of an observable random variable Y whose distribution depends on $\theta_0$. Typically Yis the value of the variable X in a repetition of the experiment.

There are several schools of statistical thinking with different views on how these problems should be done. The main schools of thought may be summarized roughly as follows:

• Neyman Pearson: In this school of thought a statistical procedure should be evaluated by its long run frequency performance. You imagine repeating the data collection exercise many times, independently. The quality of a procedure is measured by its average performance when the true distribution of the X values is $P_{\theta_0}$.

• Bayes: In this school of thought we treat $\theta$ as being random just like X. We compute the conditional distribution of what we don't know given what we do know. In particular we ask how a procedure will work on the data we actually got - no averaging over data we might have got.

• Likelihood: This school tries to combine the previous 2 by looking only at the data we actually got but trying to avoid treating $\theta$ as random.

For the next several weeks we do only the Neyman Pearson approach, though we use that approach to evaluate the quality of likelihood methods.

Likelihood

Suppose you toss a coin 6 times and get Heads twice. If p is the probability of getting H then the probability of getting 2 heads is

15p²(1-p)⁴

This probability, thought of as a function of p, is the likelihood function for this particular data.

Definition: A model is a family $\{ P_\theta; \theta \in \Theta\}$ of possible distributions for some random variable X. Typically the model is described by specifying $\{f_\theta(x); \theta \in \Theta\}$ the set of possible densities of X.

Definition: The likelihood function is the function L whose domain is $\Theta$ and whose values are given by

$$L(\theta) = f_\theta(X)$$

The key point is to think about how the density depends on $\theta$ not about how it depends on X. Notice that X, the observed value of the data, has been plugged into the formula for the density. Notice also that the coin tossing example is like this but with f being the discrete density. We use the likelihood in most of our inference problems:

1.

Point estimation: we must compute an estimate $\hat\theta = \hat\theta(X)$ which lies in $\Theta$. The maximum likelihood estimate (MLE) of $\theta$ is the value $\hat\theta$ which maximizes $L(\theta)$ over $\theta\in \Theta$ if such a $\hat\theta$ exists.

2.

Point estimation of a function of $\theta$: we must compute an estimate $\hat\phi = \hat\phi(X)$ of $\phi=g(\theta)$. We use $\hat\phi=g(\hat\theta)$ where $\hat\theta$ is the MLE of $\theta$.

3.

Interval (or set) estimation. We must compute a set C=C(X) in $\Theta$ which we think will contain $\theta_0$. We will use

$$\{\theta\in\Theta: L(\theta) > c\}$$

for a suitable c.

4.

Hypothesis testing: We must decide whether or not $\theta_0\in\Theta_0$ where $\Theta_0 \subset \Theta$. We base our decision on the likelihood ratio

$$\frac{\sup\{L(\theta); \theta \in \Theta_0\}}{ \sup\{L(\theta); \theta \in \Theta\setminus\Theta_0\}}$$

Maximum Likelihood Estimation

To find an MLE we maximize L. This is a typical function maximization problem which we approach by setting the gradient of L equal to 0 and then checking to see that the root is a maximum, not a minimum or saddle point.

We begin by examining some likelihood plots in examples:

Cauchy Data

We have a sample $X_1,\ldots,X_n$ from the Cauchy$(\theta)$ density

$$f(x;\theta) = \frac{1}{\pi(1+(x-\theta)^2)}$$

The likelihood function is

$$L(\theta) = \prod_{i=1}^n\frac{1}{\pi(1+(X_i-\theta)^2)}$$

Here are some plots of this function for 6 samples of size 5.

Here are close up views of these plots for $\theta$ between -2 and 2.

Now for sample size 25.

Here are close up views of these plots for $\theta$ between -2 and 2.

I want you to notice the following points:

• The likelihood functions have peaks near the true value of $\theta$ (which is 0 for the data sets I generated).

• The peaks are narrower for the larger sample size.

• The peaks have a more regular shape for the larger value of n.

• I actually plotted $L(\theta)/L(\hat\theta)$ which has exactly the same shape as L but runs from 0 to 1 on the vertical scale.

To maximize this likelihood we would have to differentiate L and set the result equal to 0. Notice that L is a product of n terms and the derivative will then be

$$\sum_{i=1}^n \prod_{j\neq i} \frac{1}{\pi(1+(X_j-\theta)^2)} \frac{2(X_i-\theta)}{\pi(1+(X_i-\theta)^2)^2}$$

which is quite unpleasant. It is much easier to work with the logarithm of L since the log of a product is a sum and the logarithm is monotone increasing.

Definition: The Log Likelihood function is

$$\ell(\theta) = \log(L(\theta))) \, .$$

For the Cauchy problem we have

$$\ell(\theta)= -\sum \log(1+(X_i-\theta)^2) -n\log(\pi)$$

Here are the logarithms of the likelihoods plotted above:

I want you to notice the following points:

• The log likelihood functions with n=25 have pretty smooth shapes which look rather parabolic.

• For n=5 there are plenty of local maxima and minima of $\ell$.

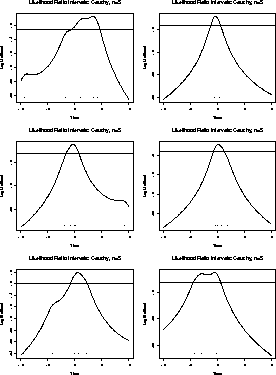
You can see that the likelihood will tend to 0 as $\vert\theta\vert\to \infty$so that the maximum of $\ell$ will occur at a root of $\ell^\prime$, the derivative of $\ell$ with respect to $\theta$.

Definition: The Score Function is the gradient of $\ell$

$$U(\theta) = \frac{\partial\ell}{\partial\theta}$$

The MLE $\hat\theta$ usually solves the Likelihood Equations

$$U(\theta)=0$$

In our Cauchy example we find

$$U(\theta) = \sum \frac{2(X_i-\theta)}{1+(X_i-\theta)^2}$$

Here are some plots of the score functions for n=5 for our Cauchy data sets. Each score is plotted beneath a plot of the corresponding $\ell$.

Notice that there are often multiple roots of the likelihood equations. Here is n=25:

The Binomial Distribution

If X has a Binomial $(n,\theta)$ distribution then
$$\begin{align*}L(\theta) & = \left( \begin{array}{c} n \\ X \end{array}\right) ... ...1-\theta) \\ U(\theta) & = \frac{X}{\theta} - \frac{n-X}{1-\theta} \end{align*}$$
The function L is 0 at $\theta=0$ and at $\theta=1$ unless X=0or X=n so for $1 \le X \le n-1$ the MLE must be found by setting U=0 and getting

$$\hat\theta = \frac{X}{n}$$

For X=n the log-likelihood has derivative

$$U(\theta) = \frac{n}{\theta} > 0$$

for all $\theta$ so that the likelihood is an increasing function of $\theta$ which is maximized at $\hat\theta=1=X/n$. Similarly when X=0 the maximum is at $\hat\theta=0=X/n$.

The Normal Distribution

Now we have $X_1,\ldots,X_n$ iid $N(\mu,\sigma^2)$. There are two parameters $\theta=(\mu,\sigma)$. We find
$$\begin{align*}L(\mu,\sigma)& = (2\pi)^{-n/2} \sigma^{-n} \exp\{-\sum(X_i-\mu)^2/... ...rac{\sum(X_i-\mu)^2}{\sigma^3} -\frac{n}{\sigma} \end{array}\right] \end{align*}$$

Notice that U is a function with two components because $\theta$ has two components.

Setting the likelihood equal to 0 and solving gives

$$\hat\mu=\bar{X}$$

and

$$\hat\sigma = \sqrt{\frac{\sum(X_i-\bar{X})^2}{n}}$$

You need to check that this is actually a maximum. To do so you compute one more derivative. The matrix H of second derivatives of $\ell$ is

$$\left[\begin{array}{cc} \frac{-n}{\sigma^2} & \frac{-2\sum(X_... ...m(X_i-\mu)^2}{\sigma^4} +\frac{n}{\sigma^2} \end{array}\right]$$

Plugging in the mle gives

$$H(\hat\theta) = \left[\begin{array}{cc} \frac{-n}{\hat\sigma^2} & 0 \\ 0 & \frac{-2n}{\hat\sigma^2} \end{array}\right]$$

This matrix is negative definite. Both its eigenvalues are negative. So $\hat\theta$ must be a local maximum.

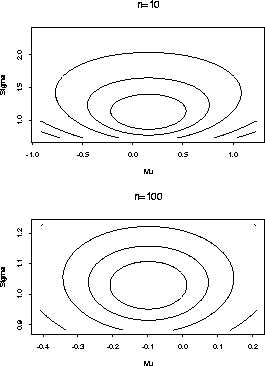
Here is a contour plot of the normal log likelihood for two data sets with n=10 and n=100.

Here are perspective plots of the same.

Notice that the contours are quite ellipsoidal for the larger sample size.

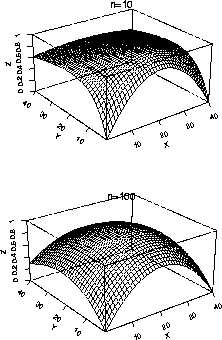
We now turn to theory to explain the features of these plots, at least approximately in large samples.