STAT 801
Problems: Assignment 3
Postscript version of these questions
- 1.
- Suppose
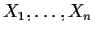 are iid real random variables with
density f . Let
are iid real random variables with
density f . Let
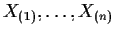 be the X's arranged
in increasing order.
be the X's arranged
in increasing order.
- (a)
- Find the joint density of
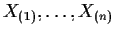 .
.
- (b)
- Suppose
f=1[0,1]. Prove that
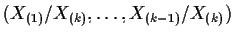 is independent of
is independent of
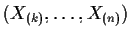 .
.
- (c)
- Find the density of X(k).
- (d)
- Find the density of
X(k)-X(j).
- 2.
- Suppose
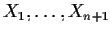 are iid exponential. Let
are iid exponential. Let
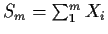 .
.
- (a)
- Find the joint density of
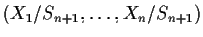 .
.
- (b)
- Find the joint density of
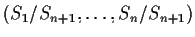 .
.
- 3.
- Suppose
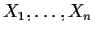 are iid N(
are iid N(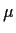 ,
,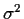 ).
Let
).
Let
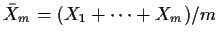 .
Let
.
Let
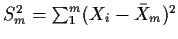 .
.
- (a)
- Develop a recurrence relation for Sm and
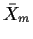 ,
expressing
Sm and
,
expressing
Sm and
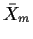 in terms of Sm-1 and
in terms of Sm-1 and
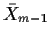 .
.
- (b)
- Find the joint density of
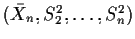 .
.
- (c)
- Generate data from N(0,1). By adding 10k to the data for
some large values of k compare the numerical performance of these
recurrence relations to that of the one pass formula using
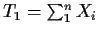 ,
,
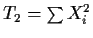 and the usual computing formulas
for the sample variance.
and the usual computing formulas
for the sample variance.
- 4.
- Suppose X and Y are iid
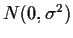 .
.
- (a)
- Show that X2+Y2 and
X/(X2+Y2)1/2 are independent.
- (b)
- Show that
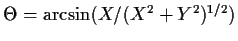 is uniformly
distributed on
is uniformly
distributed on
![$(-\pi/2,\pi/2]$](img20.gif) .
.
- (c)
- Show X/Y is a Cauchy random variable.
Richard Lockhart
1998-08-27
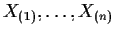 .
.
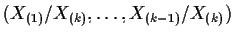 is independent of
is independent of
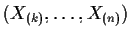 .
.
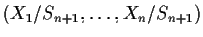 .
.
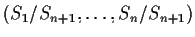 .
.
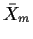 ,
expressing
Sm and
,
expressing
Sm and
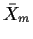 in terms of Sm-1 and
in terms of Sm-1 and
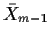 .
.
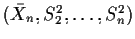 .
.
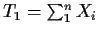 ,
,
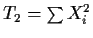 and the usual computing formulas
for the sample variance.
and the usual computing formulas
for the sample variance.
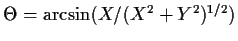 is uniformly
distributed on
is uniformly
distributed on
![$(-\pi/2,\pi/2]$](img20.gif) .
.