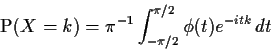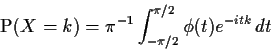STAT 801
Problems: Assignment 4
Postscript version of these questions
- 1.
- Compute the characteristic function, cumulants and central moments
for the Poisson(
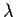 )
distribution.
)
distribution.
- 2.
- Compute the characteristic function, cumulants and central moments
for the Gamma distribution with shape parameter
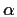 and scale parameter
and scale parameter
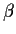 .
.
- 3.
- Develop explicit formulas for the saddlepoint approximation to the
density of the mean of a sample of size n from the exponential
distribution. Compare the results with the true Gamma density.
- 4.
- Suppose X, Y and Z are independent standard exponentials. Use
numerical Fourier inversion of the characteristic function to compute
the density of X+Y/2+Z/4 at 1. You may use the splus function
integ.romb (or any other function) found by attaching the directory
/home/math4/lockhart/research/software/quadrature/.Data.
A handout on these functions is available
here.
- 5.
- Suppose X is an integer valued random variable. Let
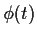 be
the characteristic function of X.
be
the characteristic function of X.
- (a)
- Show that
- (b)
- Suppose further that X is a random variable such that
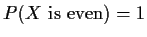 .
Show that
.
Show that
- 6.
- Suppose
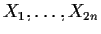 are independent random variables such that
are independent random variables such that
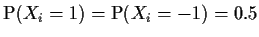 .
Prove that as
.
Prove that as
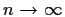
where 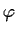 is the standard normal density.
You should use part b) of the previous
problem and Taylor expansion of the characteristic function around 0.
Also do the same thing using Sterling's formula.
is the standard normal density.
You should use part b) of the previous
problem and Taylor expansion of the characteristic function around 0.
Also do the same thing using Sterling's formula.
- 7.
- If
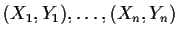 are independent bivariate normal
random variables find the limiting distribution of
are independent bivariate normal
random variables find the limiting distribution of
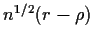 where r is the sample correlation coefficient and
where r is the sample correlation coefficient and 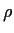 is the
population correlation. HINTS: the problem is easier for
is the
population correlation. HINTS: the problem is easier for
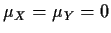 and
and
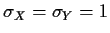 so prove that you can assume these values for
the parameters without loss of generality. Next remember that the
correlation coefficient can be computed from the 5 summary statistics
so prove that you can assume these values for
the parameters without loss of generality. Next remember that the
correlation coefficient can be computed from the 5 summary statistics
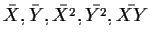 .
Use the central limit
theorem (multivariate version) to compute an approximate normal distribution
for this vector.
.
Use the central limit
theorem (multivariate version) to compute an approximate normal distribution
for this vector.
Richard Lockhart
1998-11-01

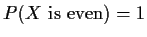 .
Show that
.
Show that