- (a)
- Find the exact confidence levels of 95% intervals based on normal
approximations to the distributions of the pivots
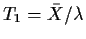 ,
T2 =1/T1, and
,
T2 =1/T1, and
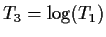 for n=10, 20 and 40.
for n=10, 20 and 40.
- (b)
- Find the shortest exact 95% confidence interval based on
T1; get numerical values for n=10, 20 and 40.
- (c)
- Find the exact confidence level of 95% confidence intervals based
on the chi-squared approximation to the distribution of deviance drop.
Compare the results with the previous question based on length and
coverage probabilities.
Figure out how to make a convincing comparison. Which method is better?
- (a)
- Show that this test is
uniformly most powerful among non-randomized tests at the level
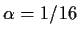 for testing p=1/2 against p>1/2.
for testing p=1/2 against p>1/2.
- (b)
- Now suppose that
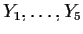 are iid Bernouilli(p). Show that the
region
are iid Bernouilli(p). Show that the
region
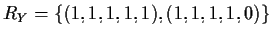 has level 1/16 and is more
powerful than the test based on RX for each p>1/2.
has level 1/16 and is more
powerful than the test based on RX for each p>1/2.
- (c)
- If
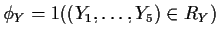 show that
show that
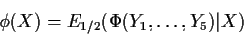
is a test function, evaluate its power and level.
is a test function and compare its power and level to that of