The Fourier series for a function ![]() truncated to order
truncated to order ![]() ,
namely
,
namely
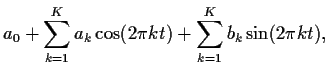
![$\displaystyle \int_0^1 \left[f(t)-f_K(t)\right]^2 \, dt
$](img6.gif)
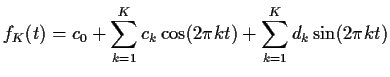
![$\displaystyle \int_0^1 \left[f(t)-f_K(t)\right]^2 \, dt
$](img6.gif) |
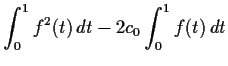 |
||
![$\displaystyle - 2 \sum_{k=1}^K \int_0^1 f(t) \left[c_k\cos(2\pi k t) + d_k \sin(2\pi k t) \right] \, dt$](img10.gif) |
This result says that a Fourier series is the best possible approximation
to a function ![]() by a trigonometric polynomial of this type.
However, the conclusion depends quite heavily on how we measure the
quality of approximation.
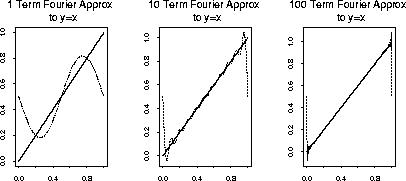
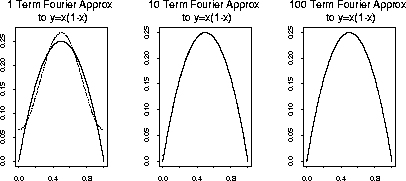
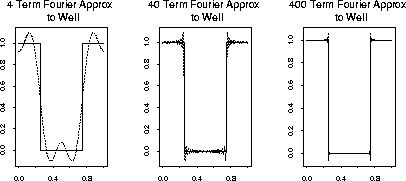
Below are Fourier approximations to each of 3 functions on [0,1]:
the line
by a trigonometric polynomial of this type.
However, the conclusion depends quite heavily on how we measure the
quality of approximation.
Below are Fourier approximations to each of 3 functions on [0,1]:
the line ![]() , the quadratic
, the quadratic ![]() and the square well
and the square well
![]() . For each plot the pictures get better as
. For each plot the pictures get better as
![]() improves. However the well shaped plot shows effects of Gibb's
phenomenon: near the discontinuity in
improves. However the well shaped plot shows effects of Gibb's
phenomenon: near the discontinuity in ![]() there is an overshoot which
is very narrow and spiky. The overshoot is of a size which does not
depend on the order of approximation.
there is an overshoot which
is very narrow and spiky. The overshoot is of a size which does not
depend on the order of approximation.
A similar discontinuity is implicit in the function ![]() since the
Fourier approximations are periodic with period 1. This means that
the approximations are equal at 0 and at 1 while
since the
Fourier approximations are periodic with period 1. This means that
the approximations are equal at 0 and at 1 while ![]() is not.
The quadratic function does have
is not.
The quadratic function does have ![]() and the Fourier
approximation is much better.
and the Fourier
approximation is much better.
My S-plus plotting code:
lin <- function(k)
{
x <- seq(0, 1, length = 5000)
kv <- 1:k
sv <- sin(2 * pi * outer(x, kv))
y <- - sv %*% (1/(pi * kv)) + 0.5
plot(x, x, xlab = "", ylab = "", main = paste(as.character(k),
"Term Fourier Approximation to y=x"), type = "l")
lines(x, y, lty = 2)
}
shows the use of the outer function and the paste function as well as
how to avoid loops using matrix arithmetic.