Virtual Library of Simulation Experiments:

Uncertainty Quantification Test Problems

Screening Test Problems

Integration Test Problems

---

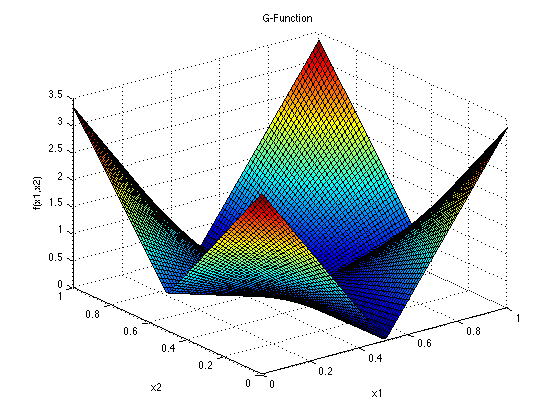
G-Function

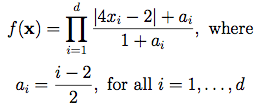
Description:

Dimensions: d

As discussed by Marrel et al. (2009), this test function is used as an integrand for various numerical estimation methods, including sensitivity analysis methods, because it is fairly complex, and its sensitivity indices can be expressed analytically. The exact value of the integral with this function as an integrand is 1.

For each index i, a lower value of a_i indicates a higher importance of the input variable x_i. Above are the values of a_i recommended by Crestaux et al. (2007).

Input Domain and Distributions:

For integration, screening and sensitivity analysis, the function is integrated over the hypercube [0, 1], for all
i = 1, …, d.

For the purposes of uncertainty quantification, the independent distributions of the input random variables are, as given by Marrel et al. (2009): x_i ~ Uniform[0, 1], for all i = 1, …, d.

Modifications and Alternative Forms:

Kucherenko et al. (2011) use the values a₀ = a₁ = 0 and a₃ = … = a_d = 6.52. When used with a_i = 6.52, for all i = 1, … d, they classify it as a Type B function, meaning that it has dominant low-order terms and a small effective dimension.

In many cases, for instance in Marrel et al. (2008), there is the constraint that a_i ≥ 0. They conclude that:

Code:

References:

Crestaux, T., Martinez, J.-M., Le Maitre, O., & Lafitte, O. (2007). Polynomial chaos expansion for uncertainties quantification and sensitivity analysis [PowerPoint slides]. Retrieved from SAMO 2007 website: http://samo2007.chem.elte.hu/lectures/Crestaux.pdf.

Davis, P. J., & Rabinowitz, P. (1984). Methods of numerical integration, second ed. New York: Academic Press.

Glen, G., & Isaacs, K. (2012). Estimating Sobol sensitivity indices using correlations. Environmental Modelling & Software.

Kucherenko, S., Feil, B., Shah, N., & Mauntz, W. (2011). The identification of model effective dimensions using global sensitivity analysis. Reliability Engineering & System Safety, 96(4), 440-449.

Marrel, A., Iooss, B., Van Dorpe, F., & Volkova, E. (2008). An efficient methodology for modeling complex computer codes with Gaussian processes. Computational Statistics & Data Analysis, 52(10), 4731-4744.

Marrel, A., Iooss, B., Laurent, B., & Roustant, O. (2009). Calculations of sobol indices for the gaussian process metamodel. Reliability Engineering & System Safety, 94(3), 742-751.

Saltelli, A., Chan, K., & Scott, E. M. (Eds.). (2000). Sensitivity analysis (Vol. 134). New York: Wiley.

Saltelli, A., & Sobol', I. Y. M. (1994). Sensitivity analysis for nonlinear mathematical models: numerical experience. Matematicheskoe Modelirovanie, 7(11), 16-28.

Saltelli, A., & Sobol', I. M. (1995). About the use of rank transformation in sensitivity analysis of model output. Reliability Engineering & System Safety, 50(3), 225-239.

---

For questions or comments, please email Derek Bingham at: dbingham@stat.sfu.ca.