Ishigami Function
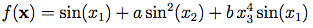
Description:
Dimensions: 3The Ishigami function of Ishigami & Homma (1990) is used as an example for uncertainty and sensitivity analysis methods, because it exhibits strong nonlinearity and nonmonotonicity. It also has a peculiar dependence on x3, as described by Sobol' & Levitan (1999).
The values of a and b used by Crestaux et al. (2007) and Marrel et al. (2009) are: a = 7 and b = 0.1. Sobol' & Levitan (1999) use a = 7 and b = 0.05.
Input Distributions:
The independent distributions of the input random variables are usually: xi ~ Uniform[-π, π], for all i = 1, 2, 3.Code:
References:
Crestaux, T., Martinez, J.-M., Le Maitre, O., & Lafitte, O. (2007). Polynomial chaos expansion for uncertainties quantification and sensitivity analysis [PowerPoint slides]. Retrieved from SAMO 2007 website: http://samo2007.chem.elte.hu/lectures/Crestaux.pdf.
Ishigami, T., & Homma, T. (1990, December). An importance quantification technique in uncertainty analysis for computer models. In Uncertainty Modeling and Analysis, 1990. Proceedings., First International Symposium on (pp. 398-403). IEEE.
Marrel, A., Iooss, B., Laurent, B., & Roustant, O. (2009). Calculations of sobol indices for the gaussian process metamodel. Reliability Engineering & System Safety, 94(3), 742-751.
Saltelli, A., Chan, K., & Scott, E. M. (Eds.). (2000). Sensitivity analysis (Vol. 134). New York: Wiley.
Sobol', I. M., & Levitan, Y. L. (1999). On the use of variance reducing multipliers in Monte Carlo computations of a global sensitivity index. Computer Physics Communications, 117(1), 52-61.
For questions or comments, please email Derek Bingham at: dbingham@stat.sfu.ca.