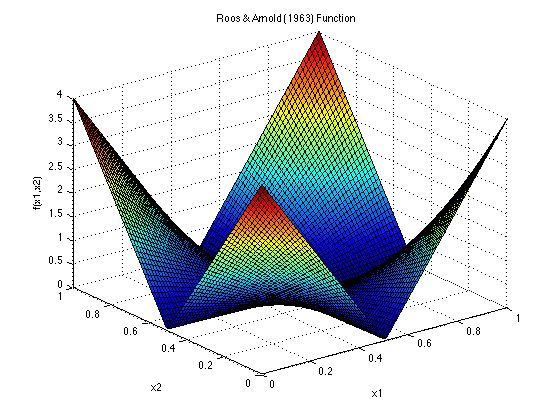
Roos & Arnold (1963) Function
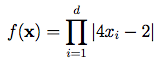
Description:
Dimensions: dThis function occurs as an integrand multiple times in the literature. The exact value of the integral with this function as an integrand is 1. The variance and variation are easily obtained, because the function is formed from the products of one-dimensional functions.
Kucherenko et al. (2011) classify it as a Type C function, meaning that it has dominant high-order interaction terms and a high effective dimension.
Input Domain:
The function is integrated over xi ∈ [0, 1], for all i = 1, …, d.Code:
References:
Bratley, P., & Fox, B. L. (1988). Algorithm 659: Implementing Sobol's quasirandom sequence generator. ACM Transactions on Mathematical Software (TOMS), 14(1), 88-100.
Bratley, P., Fox, B. L., & Niederreiter, H. (1992). Implementation and tests of low-discrepancy sequences. ACM Transactions on Modeling and Computer Simulation (TOMACS), 2(3), 195-213.
Davis, P. J., & Rabinowitz, P. (1975). Methods of numerical integration. New York: Academic Press.
Davis, P. J., & Rabinowitz, P. (1984). Methods of numerical integration, second ed. New York: Academic Press.
Fox, B. L. (1986). Algorithm 647: Implementation and relative efficiency of quasirandom sequence generators. ACM Transactions on Mathematical Software (TOMS), 12(4), 362-376.
Kucherenko, S., Feil, B., Shah, N., & Mauntz, W. (2011). The identification of model effective dimensions using global sensitivity analysis. Reliability Engineering & System Safety, 96(4), 440-449.
Morokoff, W. J., & Caflisch, R. E. (1995). Quasi-monte carlo integration. Journal of computational physics, 122(2), 218-230.
Roos, P., & Arnold, L. (1963). Numerische experimente zur mehrdimensionalen quadratur. Springer.
For questions or comments, please email Derek Bingham at: dbingham@stat.sfu.ca.