Rosenbrock Function
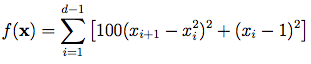
Description:
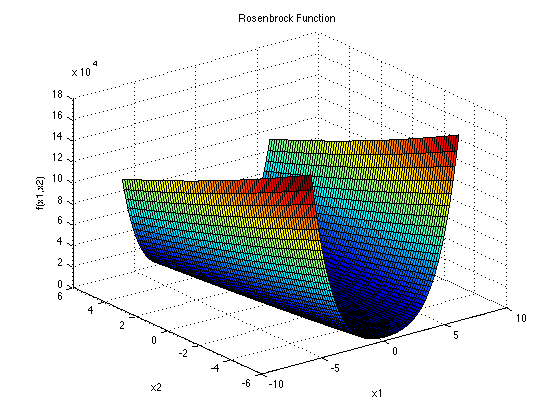
Dimensions: dThe Rosenbrock function, also referred to as the Valley or Banana function, is a popular test problem for gradient-based optimization algorithms. It is shown in the plot above in its two-dimensional form.
The function is unimodal, and the global minimum lies in a narrow, parabolic valley. However, even though this valley is easy to find, convergence to the minimum is difficult (Picheny et al., 2012).
Input Domain:
The function is usually evaluated on the hypercube xi ∈ [-5, 10], for all i = 1, …, d, although it may be restricted to the hypercube xi ∈ [-2.048, 2.048], for all i = 1, …, d.Global Minimum:
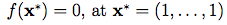
Modifications and Alternate Forms:
Picheny et al. (2012) use the following rescaled form of the function, with d = 4, on [0, 1]2: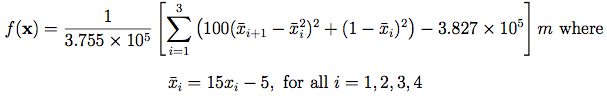
This rescaled form of the function has a mean of zero and a variance of one. The authors also add a small Gaussian error term to the output.
Code:
References:
Dixon, L. C. W., & Szego, G. P. (1978). The global optimization problem: an introduction. Towards global optimization, 2, 1-15.
Global Optimization Test Problems. Retrieved June 2013, from
http://www-optima.amp.i.kyoto-u.ac.jp/member/student/hedar/Hedar_files/TestGO.htm.
Molga, M., & Smutnicki, C. Test functions for optimization needs (2005). Retrieved June 2013, from http://www.zsd.ict.pwr.wroc.pl/files/docs/functions.pdf.
Picheny, V., Wagner, T., & Ginsbourger, D. (2012). A benchmark of kriging-based infill criteria for noisy optimization.
For questions or comments, please email Derek Bingham at: dbingham@stat.sfu.ca.
LastUpdated
Copy