Virtual Library of Simulation Experiments:

Test Functions and Datasets

Sphere Function


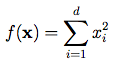
Description:

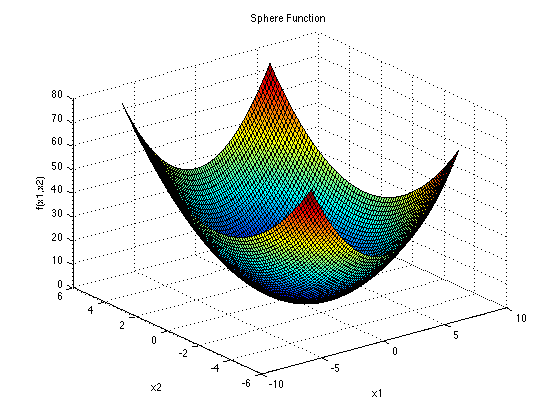
Dimensions: d

The Sphere function has d local minima except for the global one. It is continuous, convex and unimodal. The plot shows its two-dimensional form.

Input Domain:

The function is usually evaluated on the hypercube xi ∈ [-5.12, 5.12], for all i = 1, …, d.

Global Minimum:



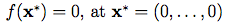
Modifications and Alternate Forms:

Picheny et al. (2012) use the following, slightly different, version of the Sphere function, with d = 6, on [0, 1]6: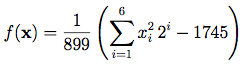

This function has a mean of zero and a variance of one. The authors also add a small Gaussian error term to the output.

Code:


References:

Dixon, L. C. W., & Szego, G. P. (1978). The global optimization problem: an introduction. Towards global optimization, 2, 1-15.

Molga, M., & Smutnicki, C. Test functions for optimization needs (2005). Retrieved June 2013, from http://www.zsd.ict.pwr.wroc.pl/files/docs/functions.pdf.

Picheny, V., Wagner, T., & Ginsbourger, D. (2012). A benchmark of kriging-based infill criteria for noisy optimization.


For questions or comments, please email Derek Bingham at: dbingham@stat.sfu.ca.



LastUpdated
Authors
Copy