| Introduction to Structural Equations with Latent Variables |
Some Measurement Models
Psychometric test theory involves many kinds of models relating
scores on psychological and educational tests to latent variables
representing intelligence or various underlying abilities.
The following example uses data on
four vocabulary tests from Lord (1957).
Tests W and X have 15 items each and are
administered with very liberal time limits.
Tests Y and Z have 75 items and
are administered under time pressure.
The covariance matrix is read by the following DATA step:
data lord(type=cov);
input _type_ $ _name_ $ w x y z;
datalines;
n . 649 . . .
cov w 86.3979 . . .
cov x 57.7751 86.2632 . .
cov y 56.8651 59.3177 97.2850 .
cov z 58.8986 59.6683 73.8201 97.8192
;
The psychometric model of interest states that W and X
are determined by a single common factor FWX, and Y
and Z are determined by a single common factor FYZ.
The two common factors are expected to have a positive correlation,
and it is desired to estimate this correlation.
It is convenient to assume that the common factors have unit variance,
so their correlation will be equal to their covariance.
The error terms for all the manifest variables are assumed to be
uncorrelated with each other and with the common factors.
The model (labeled here as Model Form D) is as follows.
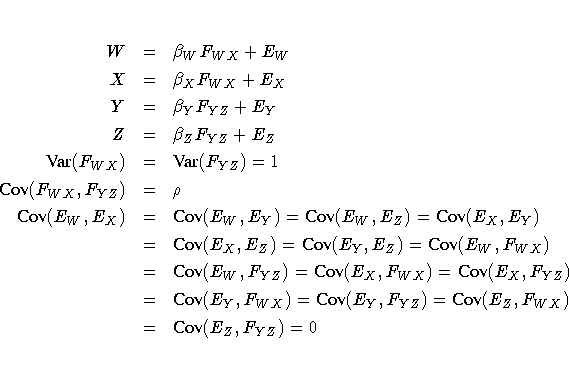
The corresponding path diagram is as follows.
Figure 14.11: Path Diagram: Lord
This path diagram can be converted to a RAM model as follows:
/* 1=w 2=x 3=y 4=z 5=fwx 6=fyz */
title 'H4: unconstrained';
proc calis data=lord cov;
ram 1 1 5 betaw,
1 2 5 betax,
1 3 6 betay,
1 4 6 betaz,
2 1 1 vew,
2 2 2 vex,
2 3 3 vey,
2 4 4 vez,
2 5 5 1,
2 6 6 1,
2 5 6 rho;
run;
Here are the major results.
|
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Fit Function |
0.0011 |
| Goodness of Fit Index (GFI) |
0.9995 |
| GFI Adjusted for Degrees of Freedom (AGFI) |
0.9946 |
| Root Mean Square Residual (RMR) |
0.2720 |
| Parsimonious GFI (Mulaik, 1989) |
0.1666 |
| Chi-Square |
0.7030 |
| Chi-Square DF |
1 |
| Pr > Chi-Square |
0.4018 |
| Independence Model Chi-Square |
1466.6 |
| Independence Model Chi-Square DF |
6 |
| RMSEA Estimate |
0.0000 |
| RMSEA 90% Lower Confidence Limit |
. |
| RMSEA 90% Upper Confidence Limit |
0.0974 |
| ECVI Estimate |
0.0291 |
| ECVI 90% Lower Confidence Limit |
. |
| ECVI 90% Upper Confidence Limit |
0.0391 |
| Probability of Close Fit |
0.6854 |
| Bentler's Comparative Fit Index |
1.0000 |
| Normal Theory Reweighted LS Chi-Square |
0.7026 |
| Akaike's Information Criterion |
-1.2970 |
| Bozdogan's (1987) CAIC |
-6.7725 |
| Schwarz's Bayesian Criterion |
-5.7725 |
| McDonald's (1989) Centrality |
1.0002 |
| Bentler & Bonett's (1980) Non-normed Index |
1.0012 |
| Bentler & Bonett's (1980) NFI |
0.9995 |
| James, Mulaik, & Brett (1982) Parsimonious NFI |
0.1666 |
| Z-Test of Wilson & Hilferty (1931) |
0.2363 |
| Bollen (1986) Normed Index Rho1 |
0.9971 |
| Bollen (1988) Non-normed Index Delta2 |
1.0002 |
| Hoelter's (1983) Critical N |
3543 |
|
Figure 14.12: Lord Data: Major Results for RAM Model, Hypothesis H4
|
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| RAM Estimates |
| Term |
Matrix |
Row |
Column |
Parameter |
Estimate |
Standard
Error |
t Value |
| 1 |
2 |
w |
1 |
F1 |
5 |
betaw |
7.50066 |
0.32339 |
23.19 |
| 1 |
2 |
x |
2 |
F1 |
5 |
betax |
7.70266 |
0.32063 |
24.02 |
| 1 |
2 |
y |
3 |
F2 |
6 |
betay |
8.50947 |
0.32694 |
26.03 |
| 1 |
2 |
z |
4 |
F2 |
6 |
betaz |
8.67505 |
0.32560 |
26.64 |
| 1 |
3 |
E1 |
1 |
E1 |
1 |
vew |
30.13796 |
2.47037 |
12.20 |
| 1 |
3 |
E2 |
2 |
E2 |
2 |
vex |
26.93217 |
2.43065 |
11.08 |
| 1 |
3 |
E3 |
3 |
E3 |
3 |
vey |
24.87396 |
2.35986 |
10.54 |
| 1 |
3 |
E4 |
4 |
E4 |
4 |
vez |
22.56264 |
2.35028 |
9.60 |
| 1 |
3 |
D1 |
5 |
D1 |
5 |
. |
1.00000 |
|
|
| 1 |
3 |
D2 |
6 |
D1 |
5 |
rho |
0.89855 |
0.01865 |
48.18 |
| 1 |
3 |
D2 |
6 |
D2 |
6 |
. |
1.00000 |
|
|
|
The same analysis can be performed with the LINEQS statement.
Subsequent analyses are illustrated with the LINEQS statement
rather than the RAM statement because it is slightly easier
to understand the constraints as written in the LINEQS
statement without constantly referring to the path diagram.
The LINEQS and RAM statements may yield slightly different
results due to the inexactness of the numerical optimization;
the discrepancies can be reduced by specifying a more
stringent convergence criterion such as GCONV=1E-4 or GCONV=1E-6.
It is convenient to create an OUTRAM= data set for use
in fitting other models with additional constraints.
title 'H4: unconstrained';
proc calis data=lord cov outram=ram4;
lineqs w=betaw fwx + ew,
x=betax fwx + ex,
y=betay fyz + ey,
z=betaz fyz + ez;
std fwx fyz=1,
ew ex ey ez=vew vex vey vez;
cov fwx fyz=rho;
run;
The LINEQS displayed output is as follows.
|
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| w |
= |
7.5007 |
* |
fwx |
+ |
1.0000 |
|
ew |
| Std Err |
|
0.3234 |
|
betaw |
|
|
|
|
| t Value |
|
23.1939 |
|
|
|
|
|
|
| x |
= |
7.7027 |
* |
fwx |
+ |
1.0000 |
|
ex |
| Std Err |
|
0.3206 |
|
betax |
|
|
|
|
| t Value |
|
24.0235 |
|
|
|
|
|
|
| y |
= |
8.5095 |
* |
fyz |
+ |
1.0000 |
|
ey |
| Std Err |
|
0.3269 |
|
betay |
|
|
|
|
| t Value |
|
26.0273 |
|
|
|
|
|
|
| z |
= |
8.6751 |
* |
fyz |
+ |
1.0000 |
|
ez |
| Std Err |
|
0.3256 |
|
betaz |
|
|
|
|
| t Value |
|
26.6430 |
|
|
|
|
|
|
| Variances of Exogenous Variables |
| Variable |
Parameter |
Estimate |
Standard
Error |
t Value |
| fwx |
|
1.00000 |
|
|
| fyz |
|
1.00000 |
|
|
| ew |
vew |
30.13796 |
2.47037 |
12.20 |
| ex |
vex |
26.93217 |
2.43065 |
11.08 |
| ey |
vey |
24.87396 |
2.35986 |
10.54 |
| ez |
vez |
22.56264 |
2.35028 |
9.60 |
| Covariances Among Exogenous Variables |
| Var1 |
Var2 |
Parameter |
Estimate |
Standard
Error |
t Value |
| fwx |
fyz |
rho |
0.89855 |
0.01865 |
48.18 |
|
Figure 14.13: Lord Data: Using LINEQS Statement for
RAM Model, Hypothesis H4
In an analysis of these data by J reskog and S
reskog and S rbom (1979,
pp. 54 -56; Loehlin 1987, pp. 84 -87), four hypotheses
are considered:
rbom (1979,
pp. 54 -56; Loehlin 1987, pp. 84 -87), four hypotheses
are considered:
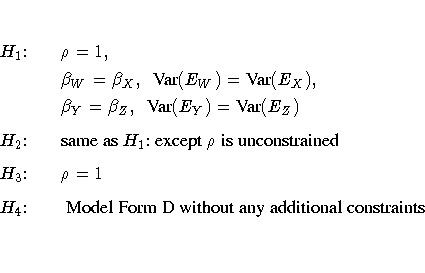
The hypothesis H3 says that there is really just one common factor
instead of two; in the terminology of test theory,
W, X, Y, and Z are said to be congeneric.
The hypothesis H2 says that W and X have the same true-scores and have
equal error variance; such tests are said to be parallel.
The hypothesis H2 also requires Y and Z to be parallel.
The hypothesis H1 says that W and X are parallel tests, Y and
Z are parallel tests, and all four tests are congeneric.
It is most convenient to fit the models in the
opposite order from that in which they are numbered.
The previous analysis fit the model for H4
and created an OUTRAM= data set called ram4.
The hypothesis H3 can be fitted directly or by modifying the ram4 data set.
Since H3 differs from H4 only in that  is
constrained to equal 1, the ram4 data set can be modified by
finding the observation for which _NAME_='rho' and changing
the variable
_NAME_ to a blank value (meaning that the observation
represents a constant rather than a parameter to be fitted)
and setting the variable _ESTIM_ to the value 1.
Both of the following analyses produce the same results:
is
constrained to equal 1, the ram4 data set can be modified by
finding the observation for which _NAME_='rho' and changing
the variable
_NAME_ to a blank value (meaning that the observation
represents a constant rather than a parameter to be fitted)
and setting the variable _ESTIM_ to the value 1.
Both of the following analyses produce the same results:
title 'H3: W, X, Y, and Z are congeneric';
proc calis data=lord cov;
lineqs w=betaw f + ew,
x=betax f + ex,
y=betay f + ey,
z=betaz f + ez;
std f=1,
ew ex ey ez=vew vex vey vez;
run;
data ram3(type=ram);
set ram4;
if _name_='rho' then
do;
_name_=' ';
_estim_=1;
end;
run;
proc calis data=lord inram=ram3 cov;
run;
The resulting output from either of these analyses is displayed
in Figure 14.14.
|
| H3: W, X, Y, and Z are congeneric |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Fit Function |
0.0559 |
| Goodness of Fit Index (GFI) |
0.9714 |
| GFI Adjusted for Degrees of Freedom (AGFI) |
0.8570 |
| Root Mean Square Residual (RMR) |
2.4636 |
| Parsimonious GFI (Mulaik, 1989) |
0.3238 |
| Chi-Square |
36.2095 |
| Chi-Square DF |
2 |
| Pr > Chi-Square |
<.0001 |
| Independence Model Chi-Square |
1466.6 |
| Independence Model Chi-Square DF |
6 |
| RMSEA Estimate |
0.1625 |
| RMSEA 90% Lower Confidence Limit |
0.1187 |
| RMSEA 90% Upper Confidence Limit |
0.2108 |
| ECVI Estimate |
0.0808 |
| ECVI 90% Lower Confidence Limit |
0.0561 |
| ECVI 90% Upper Confidence Limit |
0.1170 |
| Probability of Close Fit |
0.0000 |
| Bentler's Comparative Fit Index |
0.9766 |
| Normal Theory Reweighted LS Chi-Square |
38.1432 |
| Akaike's Information Criterion |
32.2095 |
| Bozdogan's (1987) CAIC |
21.2586 |
| Schwarz's Bayesian Criterion |
23.2586 |
| McDonald's (1989) Centrality |
0.9740 |
| Bentler & Bonett's (1980) Non-normed Index |
0.9297 |
| Bentler & Bonett's (1980) NFI |
0.9753 |
| James, Mulaik, & Brett (1982) Parsimonious NFI |
0.3251 |
| Z-Test of Wilson & Hilferty (1931) |
5.2108 |
| Bollen (1986) Normed Index Rho1 |
0.9259 |
| Bollen (1988) Non-normed Index Delta2 |
0.9766 |
| Hoelter's (1983) Critical N |
109 |
|
Figure 14.14: Lord Data: Major Results for Hypothesis H3
|
| H3: W, X, Y, and Z are congeneric |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| w |
= |
7.1047 |
* |
fwx |
+ |
1.0000 |
|
ew |
| Std Err |
|
0.3218 |
|
betaw |
|
|
|
|
| t Value |
|
22.0802 |
|
|
|
|
|
|
| x |
= |
7.2691 |
* |
fwx |
+ |
1.0000 |
|
ex |
| Std Err |
|
0.3183 |
|
betax |
|
|
|
|
| t Value |
|
22.8397 |
|
|
|
|
|
|
| y |
= |
8.3735 |
* |
fyz |
+ |
1.0000 |
|
ey |
| Std Err |
|
0.3254 |
|
betay |
|
|
|
|
| t Value |
|
25.7316 |
|
|
|
|
|
|
| z |
= |
8.5106 |
* |
fyz |
+ |
1.0000 |
|
ez |
| Std Err |
|
0.3241 |
|
betaz |
|
|
|
|
| t Value |
|
26.2598 |
|
|
|
|
|
|
| Variances of Exogenous Variables |
| Variable |
Parameter |
Estimate |
Standard
Error |
t Value |
| fwx |
|
1.00000 |
|
|
| fyz |
|
1.00000 |
|
|
| ew |
vew |
35.92087 |
2.41466 |
14.88 |
| ex |
vex |
33.42397 |
2.31038 |
14.47 |
| ey |
vey |
27.16980 |
2.24619 |
12.10 |
| ez |
vez |
25.38948 |
2.20839 |
11.50 |
|
The hypothesis H2 requires that several pairs of parameters
be constrained to have equal estimates.
With PROC CALIS, you can impose this constraint by giving the
same name to parameters that are constrained to be equal.
This can be done directly in the LINEQS and STD
statements or by using PROC FSEDIT or a DATA
step to change the values in the ram4 data set:
title 'H2: W and X parallel, Y and Z parallel';
proc calis data=lord cov;
lineqs w=betawx fwx + ew,
x=betawx fwx + ex,
y=betayz fyz + ey,
z=betayz fyz + ez;
std fwx fyz=1,
ew ex ey ez=vewx vewx veyz veyz;
cov fwx fyz=rho;
run;
data ram2(type=ram);
set ram4;
if _name_= 'betaw' then _name_='betawx';
if _name_='betax' then _name_='betawx';
if _name_='betay' then _name_='betayz';
if _name_='betaz' then _name_='betayz';
if _name_='vew' then _name_='vewx';
if _name_='vex' then _name_='vewx';
if _name_='vey' then _name_='veyz';
if _name_='vez' then _name_='veyz';
run;
proc calis data=lord inram=ram2 cov;
run;
The resulting output from either of these analyses is displayed
in Figure 14.15.
|
| H2: W and X parallel, Y and Z parallel |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Fit Function |
0.0030 |
| Goodness of Fit Index (GFI) |
0.9985 |
| GFI Adjusted for Degrees of Freedom (AGFI) |
0.9970 |
| Root Mean Square Residual (RMR) |
0.6983 |
| Parsimonious GFI (Mulaik, 1989) |
0.8321 |
| Chi-Square |
1.9335 |
| Chi-Square DF |
5 |
| Pr > Chi-Square |
0.8583 |
| Independence Model Chi-Square |
1466.6 |
| Independence Model Chi-Square DF |
6 |
| RMSEA Estimate |
0.0000 |
| RMSEA 90% Lower Confidence Limit |
. |
| RMSEA 90% Upper Confidence Limit |
0.0293 |
| ECVI Estimate |
0.0185 |
| ECVI 90% Lower Confidence Limit |
. |
| ECVI 90% Upper Confidence Limit |
0.0276 |
| Probability of Close Fit |
0.9936 |
| Bentler's Comparative Fit Index |
1.0000 |
| Normal Theory Reweighted LS Chi-Square |
1.9568 |
| Akaike's Information Criterion |
-8.0665 |
| Bozdogan's (1987) CAIC |
-35.4436 |
| Schwarz's Bayesian Criterion |
-30.4436 |
| McDonald's (1989) Centrality |
1.0024 |
| Bentler & Bonett's (1980) Non-normed Index |
1.0025 |
| Bentler & Bonett's (1980) NFI |
0.9987 |
| James, Mulaik, & Brett (1982) Parsimonious NFI |
0.8322 |
| Z-Test of Wilson & Hilferty (1931) |
-1.0768 |
| Bollen (1986) Normed Index Rho1 |
0.9984 |
| Bollen (1988) Non-normed Index Delta2 |
1.0021 |
| Hoelter's (1983) Critical N |
3712 |
|
Figure 14.15: Lord Data: Major Results for Hypothesis H2
|
| H2: W and X parallel, Y and Z parallel |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| w |
= |
7.6010 |
* |
fwx |
+ |
1.0000 |
|
ew |
| Std Err |
|
0.2684 |
|
betawx |
|
|
|
|
| t Value |
|
28.3158 |
|
|
|
|
|
|
| x |
= |
7.6010 |
* |
fwx |
+ |
1.0000 |
|
ex |
| Std Err |
|
0.2684 |
|
betawx |
|
|
|
|
| t Value |
|
28.3158 |
|
|
|
|
|
|
| y |
= |
8.5919 |
* |
fyz |
+ |
1.0000 |
|
ey |
| Std Err |
|
0.2797 |
|
betayz |
|
|
|
|
| t Value |
|
30.7215 |
|
|
|
|
|
|
| z |
= |
8.5919 |
* |
fyz |
+ |
1.0000 |
|
ez |
| Std Err |
|
0.2797 |
|
betayz |
|
|
|
|
| t Value |
|
30.7215 |
|
|
|
|
|
|
| Variances of Exogenous Variables |
| Variable |
Parameter |
Estimate |
Standard
Error |
t Value |
| fwx |
|
1.00000 |
|
|
| fyz |
|
1.00000 |
|
|
| ew |
vewx |
28.55545 |
1.58641 |
18.00 |
| ex |
vewx |
28.55545 |
1.58641 |
18.00 |
| ey |
veyz |
23.73200 |
1.31844 |
18.00 |
| ez |
veyz |
23.73200 |
1.31844 |
18.00 |
| Covariances Among Exogenous Variables |
| Var1 |
Var2 |
Parameter |
Estimate |
Standard
Error |
t Value |
| fwx |
fyz |
rho |
0.89864 |
0.01865 |
48.18 |
|
The hypothesis H1 requires one more constraint in addition to those in
H2:
title 'H1: W and X parallel, Y and Z parallel, all congeneric';
proc calis data=lord cov;
lineqs w=betawx f + ew,
x=betawx f + ex,
y=betayz f + ey,
z=betayz f + ez;
std f=1,
ew ex ey ez=vewx vewx veyz veyz;
run;
data ram1(type=ram);
set ram2;
if _name_='rho' then
do;
_name_=' ';
_estim_=1;
end;
run;
proc calis data=lord inram=ram1 cov;
run;
The resulting output from either of these analyses is displayed
in Figure 14.16.
|
| H1: W and X parallel, Y and Z parallel, all congeneric |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Fit Function |
0.0576 |
| Goodness of Fit Index (GFI) |
0.9705 |
| GFI Adjusted for Degrees of Freedom (AGFI) |
0.9509 |
| Root Mean Square Residual (RMR) |
2.5430 |
| Parsimonious GFI (Mulaik, 1989) |
0.9705 |
| Chi-Square |
37.3337 |
| Chi-Square DF |
6 |
| Pr > Chi-Square |
<.0001 |
| Independence Model Chi-Square |
1466.6 |
| Independence Model Chi-Square DF |
6 |
| RMSEA Estimate |
0.0898 |
| RMSEA 90% Lower Confidence Limit |
0.0635 |
| RMSEA 90% Upper Confidence Limit |
0.1184 |
| ECVI Estimate |
0.0701 |
| ECVI 90% Lower Confidence Limit |
0.0458 |
| ECVI 90% Upper Confidence Limit |
0.1059 |
| Probability of Close Fit |
0.0076 |
| Bentler's Comparative Fit Index |
0.9785 |
| Normal Theory Reweighted LS Chi-Square |
39.3380 |
| Akaike's Information Criterion |
25.3337 |
| Bozdogan's (1987) CAIC |
-7.5189 |
| Schwarz's Bayesian Criterion |
-1.5189 |
| McDonald's (1989) Centrality |
0.9761 |
| Bentler & Bonett's (1980) Non-normed Index |
0.9785 |
| Bentler & Bonett's (1980) NFI |
0.9745 |
| James, Mulaik, & Brett (1982) Parsimonious NFI |
0.9745 |
| Z-Test of Wilson & Hilferty (1931) |
4.5535 |
| Bollen (1986) Normed Index Rho1 |
0.9745 |
| Bollen (1988) Non-normed Index Delta2 |
0.9785 |
| Hoelter's (1983) Critical N |
220 |
|
Figure 14.16: Lord Data: Major Results for Hypothesis H1
|
| H1: W and X parallel, Y and Z parallel, all congeneric |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| w |
= |
7.1862 |
* |
fwx |
+ |
1.0000 |
|
ew |
| Std Err |
|
0.2660 |
|
betawx |
|
|
|
|
| t Value |
|
27.0180 |
|
|
|
|
|
|
| x |
= |
7.1862 |
* |
fwx |
+ |
1.0000 |
|
ex |
| Std Err |
|
0.2660 |
|
betawx |
|
|
|
|
| t Value |
|
27.0180 |
|
|
|
|
|
|
| y |
= |
8.4420 |
* |
fyz |
+ |
1.0000 |
|
ey |
| Std Err |
|
0.2800 |
|
betayz |
|
|
|
|
| t Value |
|
30.1494 |
|
|
|
|
|
|
| z |
= |
8.4420 |
* |
fyz |
+ |
1.0000 |
|
ez |
| Std Err |
|
0.2800 |
|
betayz |
|
|
|
|
| t Value |
|
30.1494 |
|
|
|
|
|
|
| Variances of Exogenous Variables |
| Variable |
Parameter |
Estimate |
Standard
Error |
t Value |
| fwx |
|
1.00000 |
|
|
| fyz |
|
1.00000 |
|
|
| ew |
vewx |
34.68865 |
1.64634 |
21.07 |
| ex |
vewx |
34.68865 |
1.64634 |
21.07 |
| ey |
veyz |
26.28513 |
1.39955 |
18.78 |
| ez |
veyz |
26.28513 |
1.39955 |
18.78 |
| Covariances Among Exogenous Variables |
| Var1 |
Var2 |
Parameter |
Estimate |
Standard
Error |
t Value |
| fwx |
fyz |
|
1.00000 |
|
|
|
The goodness-of-fit tests for the four hypotheses are summarized
in the following table.
|
|
Number of
|
|
Degrees of
|
|
|
|
Hypothesis
|
Parameters
|

|
Freedom
|
p-value
|

|
| H1 | 4 | 37.33 | 6 | 0.0000 | 1.0 |
| H2 | 5 | 1.93 | 5 | 0.8583 | 0.8986 |
| H3 | 8 | 36.21 | 2 | 0.0000 | 1.0 |
| H4 | 9 | 0.70 | 1 | 0.4018 | 0.8986 |
The hypotheses H1 and H3, which
posit  , can be rejected.
Hypotheses H2 and H4 seem to be
consistent with the available data.
Since H2 is obtained by adding four constraints to
H4, you can test H2 versus H4 by computing the
differences of the chi-square statistics and their
degrees of freedom, yielding a chi-square of 1.23 with
four degrees of freedom, which is obviously not significant.
So hypothesis H2 is consistent with the available data.
, can be rejected.
Hypotheses H2 and H4 seem to be
consistent with the available data.
Since H2 is obtained by adding four constraints to
H4, you can test H2 versus H4 by computing the
differences of the chi-square statistics and their
degrees of freedom, yielding a chi-square of 1.23 with
four degrees of freedom, which is obviously not significant.
So hypothesis H2 is consistent with the available data.
The estimates of  for H2 and H4 are almost
identical, about 0.90, indicating that the speeded and
unspeeded tests are measuring almost the same latent
variable, even though the hypotheses that stated they
measured exactly the same latent variable are rejected.
for H2 and H4 are almost
identical, about 0.90, indicating that the speeded and
unspeeded tests are measuring almost the same latent
variable, even though the hypotheses that stated they
measured exactly the same latent variable are rejected.
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
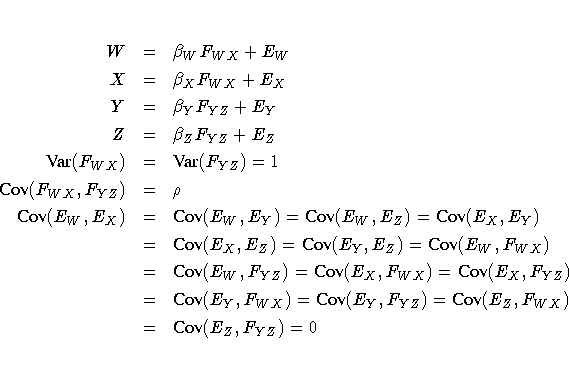

![]() reskog and S
reskog and S![]() rbom (1979,
pp. 54 -56; Loehlin 1987, pp. 84 -87), four hypotheses
are considered:
rbom (1979,
pp. 54 -56; Loehlin 1987, pp. 84 -87), four hypotheses
are considered:
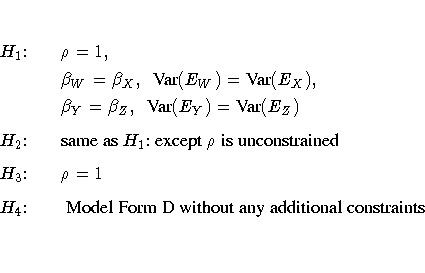
![]() is
constrained to equal 1, the ram4 data set can be modified by
finding the observation for which _NAME_='rho' and changing
the variable
_NAME_ to a blank value (meaning that the observation
represents a constant rather than a parameter to be fitted)
and setting the variable _ESTIM_ to the value 1.
Both of the following analyses produce the same results:
is
constrained to equal 1, the ram4 data set can be modified by
finding the observation for which _NAME_='rho' and changing
the variable
_NAME_ to a blank value (meaning that the observation
represents a constant rather than a parameter to be fitted)
and setting the variable _ESTIM_ to the value 1.
Both of the following analyses produce the same results:
![]() , can be rejected.
Hypotheses H2 and H4 seem to be
consistent with the available data.
Since H2 is obtained by adding four constraints to
H4, you can test H2 versus H4 by computing the
differences of the chi-square statistics and their
degrees of freedom, yielding a chi-square of 1.23 with
four degrees of freedom, which is obviously not significant.
So hypothesis H2 is consistent with the available data.
, can be rejected.
Hypotheses H2 and H4 seem to be
consistent with the available data.
Since H2 is obtained by adding four constraints to
H4, you can test H2 versus H4 by computing the
differences of the chi-square statistics and their
degrees of freedom, yielding a chi-square of 1.23 with
four degrees of freedom, which is obviously not significant.
So hypothesis H2 is consistent with the available data.
![]() for H2 and H4 are almost
identical, about 0.90, indicating that the speeded and
unspeeded tests are measuring almost the same latent
variable, even though the hypotheses that stated they
measured exactly the same latent variable are rejected.
for H2 and H4 are almost
identical, about 0.90, indicating that the speeded and
unspeeded tests are measuring almost the same latent
variable, even though the hypotheses that stated they
measured exactly the same latent variable are rejected.