Convolutions
The formulas for the binned estimator  in the previous
subsection are in the form of a convolution product between two
matrices, one of which contains the bin counts, the other of which
contains the rescaled kernels evaluated at multiples of grid
increments. This section defines these two matrices explicitly, and
shows that
in the previous
subsection are in the form of a convolution product between two
matrices, one of which contains the bin counts, the other of which
contains the rescaled kernels evaluated at multiples of grid
increments. This section defines these two matrices explicitly, and
shows that  is their convolution.
is their convolution.
Beginning with the weighted univariate case, define the
following matrices:
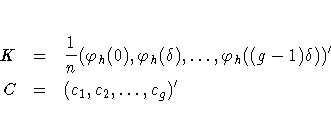
The first thing to note is that many terms in K can
practically be ignored. The term  is taken to be 0 when
is taken to be 0 when  ,so you can define
,so you can define
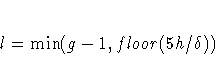
as the maximum integer multiple of the grid
increment to get nonzero evaluations
of the rescaled kernel. Here floor(x) denotes the largest
integer less than or equal to x. .
Next, let p be the smallest power of 2
that is greater than g+l+1,
-
p = 2ceil(log2 (g+l+1))
where ceil(x) denotes the smallest
integer greater than or equal to x.
Modify K as follows:
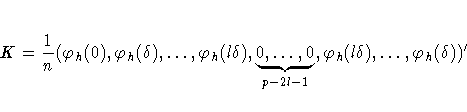
Essentially, the negligible terms of K are omitted, and the rest
are "symmetrized" (except for one term). The whole matrix is
then padded to size p×1 with zeros in the middle. The
dimension p is a highly composite number, that is, one that
decomposes into many factors, leading to the fastest Fast Fourier
Transform operation (refer to Wand 1993).
The third operation is to pad the bin count
matrix C with zeros to the same size as K:

The convolution K*C is then a p×1 matrix, and the preceding
formulas show that its first g entries are exactly the estimates
 .
.For bivariate smoothing, the matrix K is defined similarly as
-
![K = [ \kappa_{0,0} & \kappa_{0,1}
& ... &
\kappa_{0,l_{Y}} &
0
& \kappa_{0...
..._{1,l_{Y}} &
0
& \kappa_{1,l_{Y}} & ... &
\kappa_{1,1}
]_{p_{X} x p_{Y}}](images/kdeeq41.gif)
where  ,pX = 2ceil(log2 (gX+lX+1)), and so forth, and
,pX = 2ceil(log2 (gX+lX+1)), and so forth, and
 .
.The bin count matrix C is defined as
-
![C = [ c_{1,1} & c_{1,2} & ... &
c_{1,g_{Y}} & 0 & ... & 0\ c_{2,1} & c_{2,2...
... 0 & ... & 0 \ \vdots \ 0 & 0 & ... & 0 & 0 & ... & 0
]_{p_{X} x p_{Y}}](images/kdeeq44.gif)
As with the univariate case, the gX ×gY upper-left
corner of the convolution K*C is the matrix of the estimates
 .
.Most of the results in this subsection are found in Wand (1993).
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
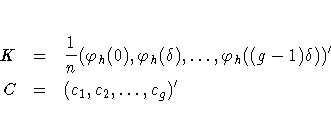
![]() is taken to be 0 when
is taken to be 0 when ![]() ,so you can define
,so you can define
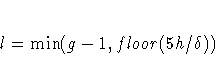
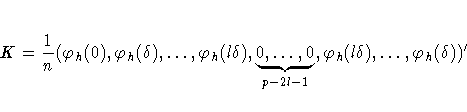

![K = [ \kappa_{0,0} & \kappa_{0,1}
& ... &
\kappa_{0,l_{Y}} &
0
& \kappa_{0...
..._{1,l_{Y}} &
0
& \kappa_{1,l_{Y}} & ... &
\kappa_{1,1}
]_{p_{X} x p_{Y}}](images/kdeeq41.gif)
![C = [ c_{1,1} & c_{1,2} & ... &
c_{1,g_{Y}} & 0 & ... & 0\ c_{2,1} & c_{2,2...
... 0 & ... & 0 \ \vdots \ 0 & 0 & ... & 0 & 0 & ... & 0
]_{p_{X} x p_{Y}}](images/kdeeq44.gif)