Fast Fourier Transform

The KDE Procedure

Fast Fourier Transform

As shown in the last subsection, kernel density estimates can be expressed as a submatrix of a certain convolution. The fast Fourier transform (FFT) is a computationally effective method for computing such convolutions. For a reference on this material, refer to Press et al. (1988).

The discrete Fourier transform of a complex vector z = (z₀, ... ,z_N-1) is the vector Z = (Z₀, ... ,Z_N-1) where

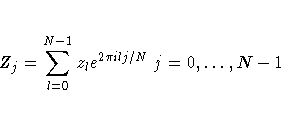
$Z_{j}=\sum_{l=0}^{N-1}z_{l}e^{2\pi ilj/N} \ j=0, ... ,N-1$

and i is the square root of -1. The vector z can be recovered from Z by applying the inverse discrete Fourier transform formula

$z_{l}=N^{-1}\sum_{j=0}^{N-1}Z_{j}e^{-2\pi ilj/N} \ l=0, ... ,N-1$

Discrete Fourier transforms and their inverses can be computed quickly using the FFT algorithm, especially when N is highly composite; that is, it can be decomposed into many factors, such as a power of 2. By the Discrete Convolution Theorem, the convolution of two vectors is the inverse Fourier transform of the element-by-element product of their Fourier transforms. This, however, requires certain periodicity assumptions, which explains why the vectors K and C require zero-padding. This is to avoid "wrap-around" effects (refer to Press et al. 1988, pp. 410 - 411). The vector K is actually mirror-imaged so that the convolution of C and K will be the vector of binned estimates. Thus, if S denotes the inverse Fourier transform of the element-by-element product of the Fourier transforms of K and C, then the first g elements of S are the estimates.

The bivariate Fourier transform of an N₁×N₂ complex matrix having (l₁+1,l₂+1) entry equal to $z_{l_{1}l_{2}}$ is the N₁×N₂ matrix with (j₁+1 ,j₂+1) entry given by

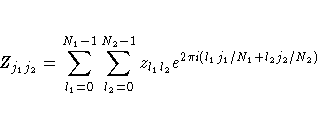
$Z_{j_{1}j_{2}}=\sum_{l_{1}=0}^{N_{1}-1} \sum_{l_{2}=0}^{N_{2}-1} z_{l_{1}l_{2}} e^{2\pi i(l_{1}j_{1}/N_{1}+l_{2}j_{2}/N_{2})}$

and the formula of the inverse is

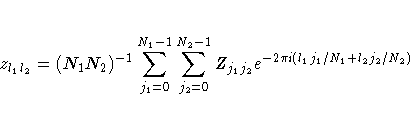
$z_{l_{1}l_{2}}=(N_{1}N_{2})^{-1} \sum_{j_{1}=0}^{N_{1}-1} \sum_{j_{2}=0}^{N_{2}-1} Z_{j_{1}j_{2}} e^{-2\pi i(l_{1}j_{1}/N_{1}+l_{2}j_{2}/N_{2})}$

The same Discrete Convolution Theorem applies, and zero-padding is needed for matrices C and K. In the case of K, the matrix is mirror-imaged twice. Thus, if S denotes the inverse Fourier transform of the element-by-element product of the Fourier transforms of K and C, then the upper-left g_X×g_Y corner of S contains the estimates.

Chapter Contents
Previous
Next
Top