Chapter Contents

Previous

Next

Polynomial Regression

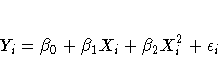
Consider the following example on population growth trends. The population of the United States from 1790 to 1970 is fit to linear and quadratic functions of time. Note that the quadratic term, YearSq, is created in the DATA step; this is done since polynomial effects such as Year*Year cannot be specified in the MODEL statement in PROC REG. The data are as follows:

   data USPopulation;
      input Population @@;
      retain Year 1780;
      Year=Year+10;
      YearSq=Year*Year;
      Population=Population/1000;
      datalines;
   3929 5308 7239 9638 12866 17069 23191 31443 39818 50155
   62947 75994 91972 105710 122775 131669 151325 179323 203211
   ;

   symbol1 c=blue;
   proc reg data=USPopulation;
      var YearSq;
      model Population=Year / r cli clm;
      plot r.*p. / cframe=ligr;
   run;

The ANOVA table is displayed in Figure 55.4.

The Model F statistic is significant (F=201.873, p<0.0001), indicating that the model accounts for a significant portion of variation in the data. The R-Square indicates that the model accounts for 92% of the variation in population growth. The fitted equation for this model is

Population = -1958.37 + 1.08 × Year

Figure 55.5 shows the confidence limits for both individual and expected values resulting from the CLM and CLI options.

The observed dependent variable is displayed for each observation along with its predicted value from the regression equation and the standard error of the mean predicted value. The 95% CL Mean columns are the confidence limits for the expected value of each observation. The 95% CL Predict columns are the confidence limits for the individual observations.

Figure 55.5 also displays the residual analysis requested by the R option.

The residual, its standard error, and the studentized residuals are displayed for each observation. The studentized residual is the residual divided by its standard error. The magnitude of each studentized residual is shown in a plot. Studentized residuals follow a t distribution and can be used to identify outlying or extreme observations. Asterisks (*) extending beyond the dashed lines indicate that the residual is more than three standard errors from zero. Many observations having absolute studentized residuals greater than 2 may indicate an inadequate model. The wave pattern seen in this plot is also an indication that the model is inadequate; a quadratic term may be needed or autocorrelation may be present in the data. Cook's D is a measure of the change in the predicted values upon deletion of that observation from the data set; hence, it measures the influence of the observation on the estimated regression coefficients. A fairly close agreement between the PRESS statistic (see Table 55.5) and the Sum of Squared Residuals indicates that the MSE is a reasonable measure of the predictive accuracy of the fitted model (Neter, Wasserman, and Kutner, 1990).

A plot of the residuals versus predicted values is shown in Figure 55.6.

The wave pattern of the studentized residual plot is seen here again. The semi-circle shape indicates an inadequate model; perhaps additional terms (such as the quadratic) are needed, or perhaps the data need to be transformed before analysis. If a model fits well, the plot of residuals against predicted values should exhibit no apparent trends.

Using the interactive feature of PROC REG, the following commands add the variable YearSq to the independent variables and refit the model.

   add YearSq;
   print;
   plot / cframe=ligr;
   run;

Figure 55.7 displays the ANOVA table and estimates for the new model.

The overall F statistic is still significant (F=4641.719, p<0.0001). The R-square has increased from 0.9223 to 0.9983, indicating that the model now accounts for 99.8% of the variation in Population. All effects are significant with p<0.0001 for each effect in the model.

The fitted equation is now

Population = 20450 - 22.781 × Year + 0.006 × Yearsq

The confidence limits and residual analysis for the second model are displayed in Figure 55.8.

The plot of the studentized residuals shows that the wave structure is gone. The PRESS statistic is much closer to the Sum of Squared Residuals now, and both statistics have been dramatically reduced. Most of the Cook's D statistics have also been reduced.

The plot of residuals versus predicted values seen in Figure 55.9 has improved since a major trend is no longer visible.

To create a plot of the observed values, predicted values, and confidence limits against Year all on the same plot and to exert some control over the look of the resulting plot, you can submit the following statements.

   symbol1 v=dot     c=yellow h=.3;
   symbol2 v=square  c=red;
   symbol3 f=simplex c=blue  h=2 v='-';
   symbol4 f=simplex c=blue  h=2 v='-';
   plot (Population predicted. u95. l95.)*Year
        / overlay cframe=ligr;
   run;

The SYMBOL statements requests that the actual data be displayed as dots, the predicted values as squares, and the upper and lower 95% confidence limits for an individual value (sometimes called a prediction interval) as dashes. PROC REG provides the short-hand commands CONF and PRED to request confidence and prediction intervals for simple regression models; see the "PLOT Statement" section for details.

To complete an analysis of these data, you may want to examine influence statistics and, since the data are essentially time series data, examine the Durbin-Watson statistic. You might also want to examine other residual plots, such as the residuals vs. regressors.

Chapter Contents

Previous

Next

Top

Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.