Example 68.1: Correlations among Physical Variables
The following data are correlations among eight physical variables as given by
Harman (1976). The first PROC VARCLUS run clusters on the basis of
principal components, the second run clusters on the basis of centroid
components. The third
analysis is hierarchical, and the TREE procedure is used to print a
tree diagram. The results of the analyses follow.
data phys8(type=corr);
title 'Eight Physical Measurements on 305 School Girls';
title2 'Harman: Modern Factor Analysis, 3rd Ed, p22';
label height='Height'
arm_span='Arm Span'
forearm='Length of Forearm'
low_leg='Length of Lower Leg'
weight='Weight'
bit_diam='Bitrochanteric Diameter'
girth='Chest Girth'
width='Chest Width';
input _name_ $ 1-8
(height arm_span forearm low_leg weight bit_diam
girth width)(7.);
_type_='corr';
datalines;
height 1.0 .846 .805 .859 .473 .398 .301 .382
arm_span.846 1.0 .881 .826 .376 .326 .277 .415
forearm .805 .881 1.0 .801 .380 .319 .237 .345
low_leg .859 .826 .801 1.0 .436 .329 .327 .365
weight .473 .376 .380 .436 1.0 .762 .730 .629
bit_diam.398 .326 .319 .329 .762 1.0 .583 .577
girth .301 .277 .237 .327 .730 .583 1.0 .539
width .382 .415 .345 .365 .629 .577 .539 1.0
;
proc varclus data=phys8;
run;
The PROC VARCLUS statement invokes the procedure. By default,
PROC VARCLUS clusters on the basis of principal components.
Output 68.1.1: Principal Cluster Components: Cluster Summary
|
| Eight Physical Measurements on 305 School Girls |
| Harman: Modern Factor Analysis, 3rd Ed, p22 |
| Oblique Principal Component Cluster Analysis |
| Cluster summary for 1 cluster |
| Cluster |
Members |
Cluster
Variation |
Variation
Explained |
Proportion
Explained |
Second
Eigenvalue |
| 1 |
8 |
8 |
4.67288 |
0.5841 |
1.7710 |
| Total variation explained = 4.67288 Proportion = 0.5841 |
| Cluster summary for 2 clusters |
| Cluster |
Members |
Cluster
Variation |
Variation
Explained |
Proportion
Explained |
Second
Eigenvalue |
| 1 |
4 |
4 |
3.509218 |
0.8773 |
0.2361 |
| 2 |
4 |
4 |
2.917284 |
0.7293 |
0.4764 |
| Total variation explained = 6.426502 Proportion = 0.8033 |
| Cluster |
Variable |
R-squared with |
1-R**2
Ratio |
Variable
Label |
Own
Cluster |
Next
Closest |
| Cluster 1 |
height |
0.8777 |
0.2088 |
0.1545 |
Height |
| |
arm_span |
0.9002 |
0.1658 |
0.1196 |
Arm Span |
| |
forearm |
0.8661 |
0.1413 |
0.1560 |
Length of Forearm |
| |
low_leg |
0.8652 |
0.1829 |
0.1650 |
Length of Lower Leg |
| Cluster 2 |
weight |
0.8477 |
0.1974 |
0.1898 |
Weight |
| |
bit_diam |
0.7386 |
0.1341 |
0.3019 |
Bitrochanteric Diameter |
| |
girth |
0.6981 |
0.0929 |
0.3328 |
Chest Girth |
| |
width |
0.6329 |
0.1619 |
0.4380 |
Chest Width |
| No cluster meets the criterion for splitting. |
|
As displayed in Output 68.1.1, the cluster component (by default,
the first principal component) explains 58.41% of the total variation
in the 8 variables.
The cluster is split because the second eigenvalue is greater
than 1 (the default value of the MAXEIGEN option).
The two resulting cluster components explain 80.33% of the variation in the
original variables. The cluster summary table
shows that the variables height, arm_span, forearm,
and low_leg have
been assigned to the first cluster; and that the variables weight,
bit_diam, girth, and width have been assigned to the
second cluster.
Output 68.1.2: Standard Scoring Coefficients and Cluster Structure Table
|
| Oblique Principal Component Cluster Analysis |
| Standardized Scoring Coefficients |
| Cluster |
|
1 |
2 |
| height |
Height |
0.266977 |
0.000000 |
| arm_span |
Arm Span |
0.270377 |
0.000000 |
| forearm |
Length of Forearm |
0.265194 |
0.000000 |
| low_leg |
Length of Lower Leg |
0.265057 |
0.000000 |
| weight |
Weight |
0.000000 |
0.315597 |
| bit_diam |
Bitrochanteric Diameter |
0.000000 |
0.294591 |
| girth |
Chest Girth |
0.000000 |
0.286407 |
| width |
Chest Width |
0.000000 |
0.272710 |
| Cluster Structure |
| Cluster |
|
1 |
2 |
| height |
Height |
0.936881 |
0.456908 |
| arm_span |
Arm Span |
0.948813 |
0.407210 |
| forearm |
Length of Forearm |
0.930624 |
0.375865 |
| low_leg |
Length of Lower Leg |
0.930142 |
0.427715 |
| weight |
Weight |
0.444281 |
0.920686 |
| bit_diam |
Bitrochanteric Diameter |
0.366201 |
0.859404 |
| girth |
Chest Girth |
0.304779 |
0.835529 |
| width |
Chest Width |
0.402430 |
0.795572 |
|
The standardized scoring
coefficients in Output 68.1.2
show that each cluster component has similar scores
for each of its associated variables. This suggests that the principal cluster
component solution should be similar to the centroid cluster
component solution, which follows in the next PROC VARCLUS run.
The cluster structure table displays high correlations between
the variables and their own cluster component. The correlations between
the variables and the opposite cluster component are all moderate.
Output 68.1.3: Inter-Cluster Correlations
|
| Oblique Principal Component Cluster Analysis |
| Inter-Cluster Correlations |
| Cluster |
1 |
2 |
| 1 |
1.00000 |
0.44513 |
| 2 |
0.44513 |
1.00000 |
|
The intercluster correlation table shows that the cluster components
are moderately correlated with 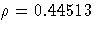 .
.In the following statements, the CENTROID option in the PROC VARCLUS statement
specifies that cluster centroids be used as the basis for clustering.
proc varclus data=phys8 centroid;
run;
Output 68.1.4: Centroid Cluster Components: Cluster Summary
|
| Oblique Centroid Component Cluster Analysis |
| Cluster summary for 1 cluster |
| Cluster |
Members |
Cluster
Variation |
Variation
Explained |
Proportion
Explained |
| 1 |
8 |
8 |
4.631 |
0.5789 |
| Total variation explained = 4.631 Proportion = 0.5789 |
| Cluster summary for 2 clusters |
| Cluster |
Members |
Cluster
Variation |
Variation
Explained |
Proportion
Explained |
| 1 |
4 |
4 |
3.509 |
0.8773 |
| 2 |
4 |
4 |
2.91 |
0.7275 |
| Total variation explained = 6.419 Proportion = 0.8024 |
| Cluster |
Variable |
R-squared with |
1-R**2
Ratio |
Variable
Label |
Own
Cluster |
Next
Closest |
| Cluster 1 |
height |
0.8778 |
0.2075 |
0.1543 |
Height |
| |
arm_span |
0.8994 |
0.1669 |
0.1208 |
Arm Span |
| |
forearm |
0.8663 |
0.1410 |
0.1557 |
Length of Forearm |
| |
low_leg |
0.8658 |
0.1824 |
0.1641 |
Length of Lower Leg |
| Cluster 2 |
weight |
0.8368 |
0.1975 |
0.2033 |
Weight |
| |
bit_diam |
0.7335 |
0.1341 |
0.3078 |
Bitrochanteric Diameter |
| |
girth |
0.6988 |
0.0929 |
0.3321 |
Chest Girth |
| |
width |
0.6473 |
0.1618 |
0.4207 |
Chest Width |
|
The first cluster component, which, in the centroid method,
is an unweighted sum of the standardized variables, explains 57.89% of
the variation in the data. This value is near the maximum possible
variance explained, 58.41%, which is attained by the first
principal component (Output 68.1.1).
The centroid clustering algorithm splits the
variables into the same two clusters created in the principal component
method. Recall that this outcome was suggested by the
similar standardized scoring coefficients in the principal
cluster component solution.
The default behavior in the centroid method is to
split any cluster with less than 75% of the total cluster variance
explained by the centroid component. In the next step,
the second cluster, with a component that
explains only 72.75% of the total variation of
the cluster, is split.
In the R-squared table for two clusters, the width variable has
a weaker relation to its cluster than any other variable; in the three
cluster solution this variable is in a cluster of its own.
Output 68.1.5: Standardized Scoring Coefficients
|
| Oblique Centroid Component Cluster Analysis |
| Standardized Scoring Coefficients |
| Cluster |
|
1 |
2 |
| height |
Height |
0.266918 |
0.000000 |
| arm_span |
Arm Span |
0.266918 |
0.000000 |
| forearm |
Length of Forearm |
0.266918 |
0.000000 |
| low_leg |
Length of Lower Leg |
0.266918 |
0.000000 |
| weight |
Weight |
0.000000 |
0.293105 |
| bit_diam |
Bitrochanteric Diameter |
0.000000 |
0.293105 |
| girth |
Chest Girth |
0.000000 |
0.293105 |
| width |
Chest Width |
0.000000 |
0.293105 |
|
Each cluster component (Output 68.1.5)
is an unweighted average of the cluster's standardized variables.
Thus, the coefficients for each of the cluster's
associated variables are identical in the centroid
cluster component solution.
Output 68.1.6: Cluster Summary for Three Clusters
|
| Oblique Centroid Component Cluster Analysis |
| Cluster summary for 3 clusters |
| Cluster |
Members |
Cluster
Variation |
Variation
Explained |
Proportion
Explained |
| 1 |
4 |
4 |
3.509 |
0.8773 |
| 2 |
3 |
3 |
2.383333 |
0.7944 |
| 3 |
1 |
1 |
1 |
1.0000 |
| Total variation explained = 6.892333 Proportion = 0.8615 |
| Cluster |
Variable |
R-squared with |
1-R**2
Ratio |
Variable
Label |
Own
Cluster |
Next
Closest |
| Cluster 1 |
height |
0.8778 |
0.1921 |
0.1513 |
Height |
| |
arm_span |
0.8994 |
0.1722 |
0.1215 |
Arm Span |
| |
forearm |
0.8663 |
0.1225 |
0.1524 |
Length of Forearm |
| |
low_leg |
0.8658 |
0.1668 |
0.1611 |
Length of Lower Leg |
| Cluster 2 |
weight |
0.8685 |
0.3956 |
0.2175 |
Weight |
| |
bit_diam |
0.7691 |
0.3329 |
0.3461 |
Bitrochanteric Diameter |
| |
girth |
0.7482 |
0.2905 |
0.3548 |
Chest Girth |
| Cluster 3 |
width |
1.0000 |
0.4259 |
0.0000 |
Chest Width |
|
The centroid method stops at the three cluster solution.
As displayed in Output 68.1.6 and
Output 68.1.7, the three centroid components account for
86.15% of the variability in the eight variables, and all cluster
components account for at least 79.44% of the total variation in the
corresponding cluster. Additionally, the smallest correlation
between the variables and their own cluster component is
0.7482.
Output 68.1.7: Cluster Quality Table
|
| Oblique Centroid Component Cluster Analysis |
Number
of
Clusters |
Total
Variation
Explained
by Clusters |
Proportion
of Variation
Explained
by Clusters |
Minimum
Proportion
Explained
by a Cluster |
Minimum
R-squared
for a
Variable |
Maximum
1-R**2 Ratio
for a
Variable |
| 1 |
4.631000 |
0.5789 |
0.5789 |
0.4306 |
|
| 2 |
6.419000 |
0.8024 |
0.7275 |
0.6473 |
0.4207 |
| 3 |
6.892333 |
0.8615 |
0.7944 |
0.7482 |
0.3548 |
|
Note that, if the proportion option were set to a value between 0.5789
(the proportion of variance explained in the 1-cluster solution)
and 0.7275
(the minimum proportion of variance explained in the 2-cluster
solution),
PROC VARCLUS would stop at a two cluster solution, and the centroid
solution would find the same clusters as the principal components
solution.
In the following statements, the MAXC= option computes all clustering
solutions, from one to eight clusters. The SUMMARY option suppresses
all output except the final cluster quality table, and the OUTTREE=
option saves the results of the analysis to an output data set and
forces the clusters to be hierarchical. The TREE procedure is
invoked to produce a graphical display of the clusters.
proc varclus data=phys8 maxc=8 summary outtree=tree;
run;
goptions ftext=swiss;
axis2 minor=none;
axis1 label=('Proportion of Variation Explained') minor=none;
proc tree horizontal vaxis=axis2 haxis=axis1 lines=(width=2);
height _propor_;
run;
Output 68.1.8: Hierarchical Clusters and the SUMMARY Option
|
| Oblique Principal Component Cluster Analysis |
Number
of
Clusters |
Total
Variation
Explained
by Clusters |
Proportion
of Variation
Explained
by Clusters |
Minimum
Proportion
Explained
by a Cluster |
Maximum
Second
Eigenvalue
in a Cluster |
Minimum
R-squared
for a
Variable |
Maximum
1-R**2 Ratio
for a
Variable |
| 1 |
4.672880 |
0.5841 |
0.5841 |
1.770983 |
0.3810 |
|
| 2 |
6.426502 |
0.8033 |
0.7293 |
0.476418 |
0.6329 |
0.4380 |
| 3 |
6.895347 |
0.8619 |
0.7954 |
0.418369 |
0.7421 |
0.3634 |
| 4 |
7.271218 |
0.9089 |
0.8773 |
0.238000 |
0.8652 |
0.2548 |
| 5 |
7.509218 |
0.9387 |
0.8773 |
0.236135 |
0.8652 |
0.1665 |
| 6 |
7.740000 |
0.9675 |
0.9295 |
0.141000 |
0.9295 |
0.2560 |
| 7 |
7.881000 |
0.9851 |
0.9405 |
0.119000 |
0.9405 |
0.2093 |
| 8 |
8.000000 |
1.0000 |
1.0000 |
0.000000 |
1.0000 |
0.0000 |
|
The principal component method first separates the variables into
the same two clusters that were created in the first PROC VARCLUS run.
Note that, in creating the third cluster, the
principal component method identifies the variable width.
This is the same variable that is put into its own cluster in the
preceding centroid method example.
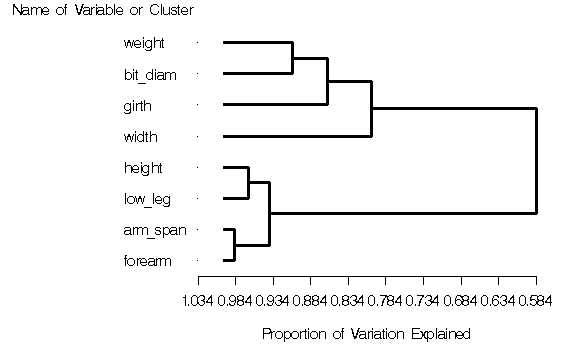
Output 68.1.9: TREE Diagram from PROC TREE
The tree diagram in Output 68.1.9 displays the cluster hierarchy.
It is clear from the diagram that there are two, or possibly
three, clusters present. However, the MAXC=8 option forces PROC VARCLUS
to split the clusters until each variable is in its own cluster.
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.