Simulated Tempering Without Normalizing Constants (STWNC)
When it comes to sampling from multi-modal distributions, single chain MCMC methods fail to efficiently explore the posterior surface. Tempering methods have been proposed to deal with problems of sampling from multi-modal target distributions. In this project with Dr Dave Campbell, we propose a new general methodology that simultaneously estimates parameters of interest and marginal likelihood that is crucial for obtaining Bayes Factors. This methodology proposes a hybrid algorithm between the two powerful tempering methods Simulated Tempering and Parallel Tempering. We refer to the new algorythm as PT-STWNC.
Our proposed Simulated Tempering algorithm introduces a continuous temperature variable to avoid the two requirements of the standard Simulated Tempering: finding an optimal temperature schedule and calculating normalizing constants. Using continuous temperature avoids discretization of the Thermodynamic Integral required by Parallel Tempering for marginal likelihood estimation, thus enabling our proposed algorithm to solve the thermodynamic integral directly and produce marginal likelihood estimates at no additional computational cost. The algorithm is illustrated in several scenarios.
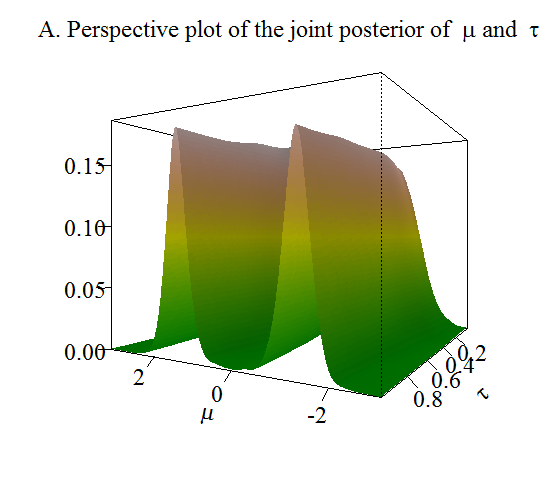
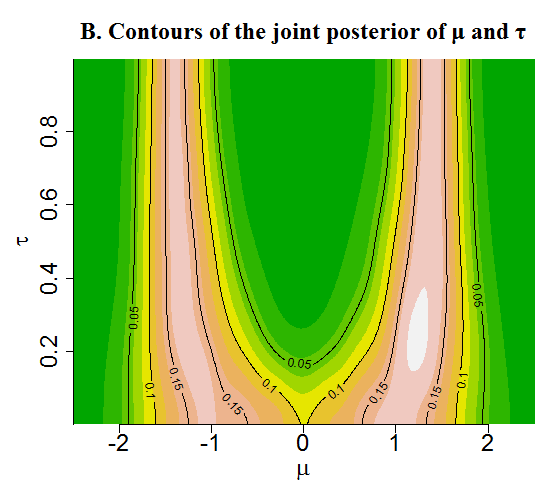
The first scenario is a bimodal model with equal modes. The perspective plot of the joint posterior distribution of the mean and the temperature parameter are given in the following figure.


The second scenario is a mixture of Gaussian models applied on Galaxy data. The complexity of the model with three components and unequal variances can be seen from the posterior samples of the marginal distributions (diagonal plots) and joint bivariate distributions (off-diagonal plots) of the first two component means, the temperature parameter and the the first variance parameter.
The third scenario involves an epidemiological Susceptible-Infected-Removed ordinary differential equation (SIR-ODE) model applied on the black plague data. The ordinary differential equation models require numerical solving the differential equation system for each evaluation of the model. The mixture of continuous and discrete parameters in the model induces multi-modality. Our algorithm succesfully samples from all the modes in the posterior space.
Incremental Mixture Importance Sampling with Shotgun optimization (IMIS-ShOpt)
Sampling from posterior density is challenging when the posterior modes are separated with deep valleys of near zero probabilities. Importance sampling algorithms such as Sampling Importance Re-sampling (SIR) or Sequential Monte Carlo variants (SMC) are more efficient alternatives than random walk algorithms that take advantage of computing the sampling weights in parallel. Under a diffused prior, the Incremental Mixture of Importance Sampling with Optimization (IMIS-Opt) is able to discover all the important posterior modes. However, if the prior disagrees with the likelihood, i.e., if the prior covers only one of the local modes in the likelihood, then either the SIR particles will degenerate or the SIR sampler will miss the important modes. As a remedy, one can choose a diffuse prior, but this implies that the prior should be chosen for algorithmic convenience rather than to represent the expert opinion.
In this project with Dr Dave Campbell, we propose a new general optimization methodology which modifies the optimization step of the IMIS-Opt algorithm to balance the discovery of global and local maxima in complex posterior topologies. We refer to the new algorythm as IMIS-ShOpt. The IMIS-ShOpt removes the dependence on the prior. The IMIS-ShOpt is tested on several examples involving ordinary differential equations.
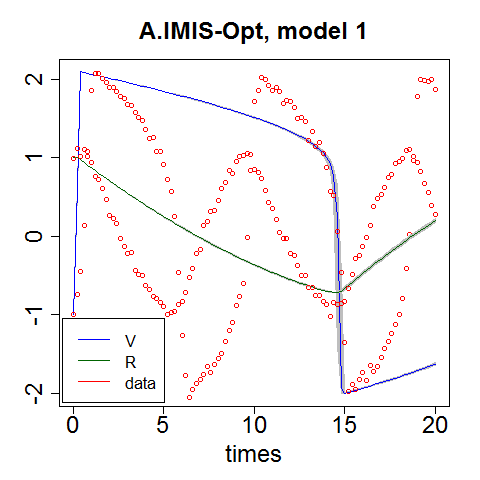
The following plots present sampled trajectories of the FitzHugh-Nagumo model obtained from the IMIS-Opt and our proposed IMIS-Shopt algorithm. This is an example where the prior disagrees with likelihood and the resulting posterior exhibit deep valleys with near-zero probabilities between the global and local modes. The IMIS-Opt algorythm gets trapped in one of the local modes, while the IMIS-ShOpt samples from all the modes. The red points correspond to data.
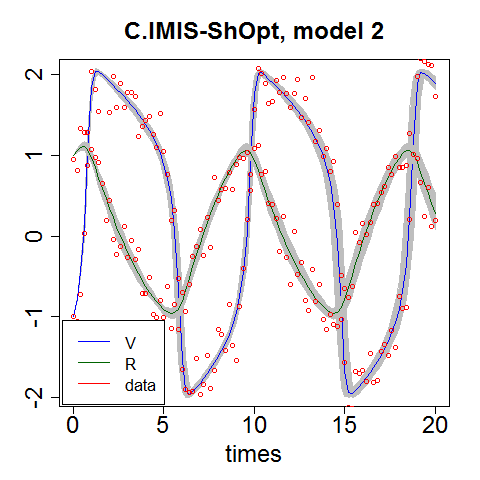
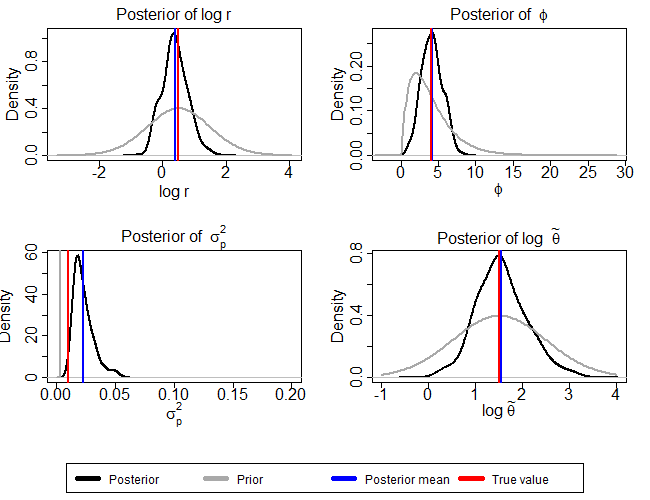
In the following scenario the IMIS-ShOpt combined with Approximate Bayesian Computation framework (refereed as IMIS-ShOpt-ABC) tackles the problem of model selection in likelihood free models. The IMIS-ShOpt-ABC provides parameter estimates and posterior probabilities of two nested models. The IMIS-ShOpt-ABC is illustrated using ecological models, the theta-Ricker (the full model) and Riker model (the restricted model), where the data were simulaed from the full model.
Marginal posterior distributions of the parameters of the theta-Ricker model are given in the following figure:
Marginal posterior distributions of the parameters of the Ricker model are given in the following figure:
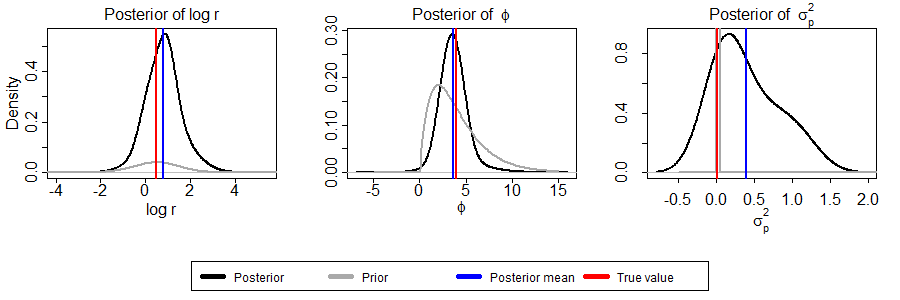
The posterior probabilites of models indicate that the full model is the 'selected' model.
Multi-modal Bayesian Information Criterion (MBIC)
The Bayesian Information Criterion (BIC) is a computationally efficient model selection tool, because it approximates the posterior probability of the model while avoiding Monte Carlo simulations over parameter space. However, when the posterior distribution is multi-modal, model selection from the BIC is based on only one mode, which leads to inaccurately estimating the posterior probability of the model, and consequently, it may result in selecting the incorrect model. This is a direct consequence of the BIC relying on the Laplace Approximation (LA) which works under the assumption that the posterior distribution is unimodal. In this project with Dr David Sivak, Dr Dave Campbell and Dr Nathan Babcock we propose a multi-modal BIC which takes into account all the relevant posterior modes, thus extending the model selection abilities of the BIC to the cases where the posterior space is multi-modal.
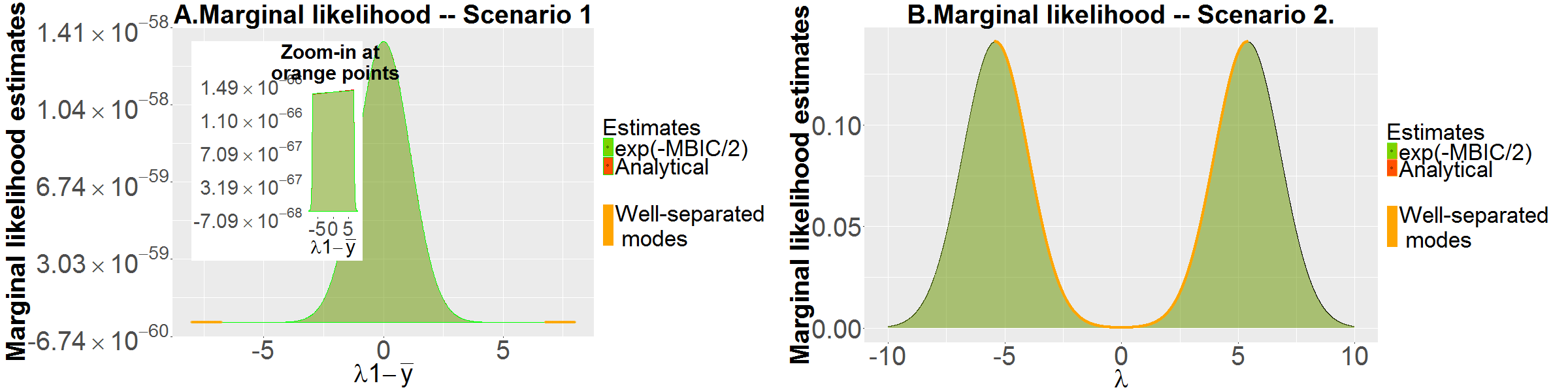
The figures below demonstrates that the LA, and hence, the BIC, produce biased estimate of the marginal likelihood of the model in the cases when the model is bimodal. The Scenario 1 in the plot A corresponds to a bimodal model with bimodal prior and unimodal likelihood; the Scenario 2 in the plot B corresponds to a bimodal model with bimodal likelihood and unimodal prior.
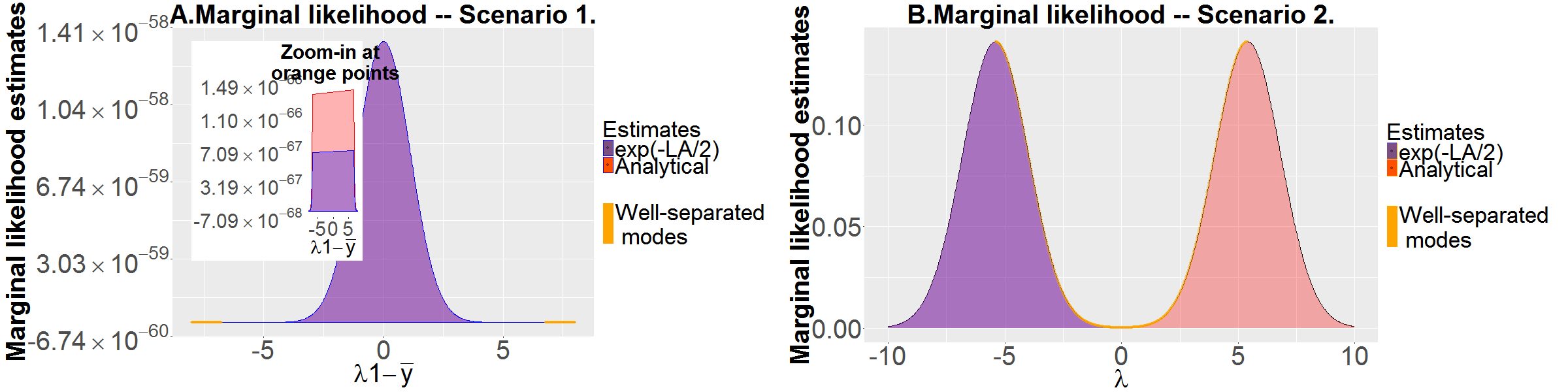
The proposed MBIC provides unbiased estimate of the posterior probability of the model when model is bimodal, provided that modes are well separated. The MBIC collapses to the unimodal LA when the posterior is unimodal.