Difference sets are highly structured objects whose study lies at the intersection of design theory, coding theory, finite geometry and algebraic number theory. Until 1997, the only groups for which necessary and sufficient conditions were known for the existence of (v, k, λ) difference sets were abelian groups of order 2^2d+2 (giving difference sets with Hadamard parameters), a result which had taken decades to establish.

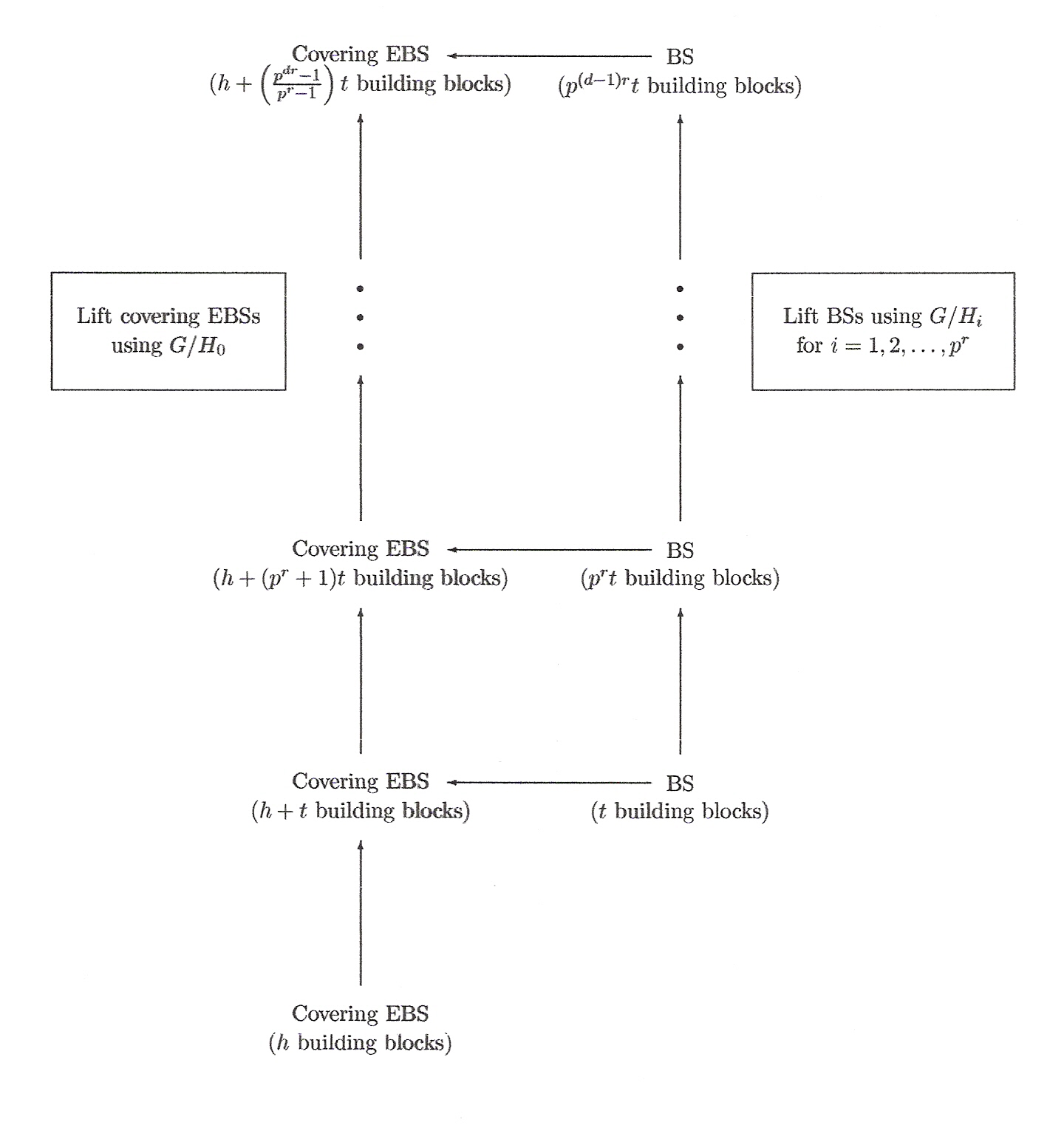
In 1997, Jim Davis and I presented a recursive construction for difference sets (and later gave a gentler overview) which unified the Hadamard, McFarland and Spence parameter families and dealt with all abelian groups known to contain such difference sets. We found a new infinite family of difference sets and included them in the unified framework. We also constructed new McFarland difference sets; when combined with a nonexistence result due to Ma and Schmidt, this gave necessary and sufficient conditions for an abelian group of order 2^2d+3(2^2d+1+1)/3 to contain a McFarland difference set.

Chen extended the construction to produce a further new parameter family of difference sets. Ionin developed it further to construct several new parameter families of symmetric designs.